文章目录

1. 为什么说“因子不是指标”？
2. 因子为什么会漂移？
3. 为什么 99% 因子没用？
4. 动量因子实战（从构造 → 清洗 → 分组 → 验证）

一、为什么说“因子不是指标”？

如果一个程序员用指标编写策略，通常如下所示：

if rsi > 70:
    sell()

这是“看到图 → 做决策”。但量化不会直接使用 RSI、MACD 等图表指标（文章末尾有对这两个指标的详细解释）。简单来说，RSI 用于衡量“近期涨幅是否过快或跌幅是否过急”，数值通常在 0–100 之间；MACD 用于观察“趋势的强度和反转”，通过两条移动平均线的差异来判断市场情况。它们有两个主要缺点：1）不稳定；2）无法标准化处理。

例如，两支股票：

• A 股票 10 元
• B 股票 1000 元

使用 RSI 得到的“70”与“70”并不表示相同的风险状况。更重要的是，你无法将它们视为“可比较的数值特征”。而因子是什么？因子是结构化信息。例如，动量因子（30 日涨幅）：“动量因子”的含义是：近期涨幅较大的股票，未来更有可能继续上涨；近期跌幅较大的股票，未来更有可能继续下跌。简单地统计：“过去 30 天谁涨得最猛？”——将这个数字作为特征，用于排序股票。

momentum = close.pct_change(30).shift(1)

这行代码包含了三个关键点：1）pct_change —— 描述“相对变化”；2）30 —— 使用过去 30 天构建特征；3）shift(1) —— 确保使用的是“当时可见的数据”。你不是在“看图”，而是在构建一个对所有股票都统一尺度、可排序、可比较、可统计的数值。如果你熟悉机器学习，你会发现：这与构建一个特征（feature）非常相似。指标告诉你“它长这样”。因子告诉你“它在特征空间中的排名”。这就是本质区别。

二、因子为什么会漂移？

因子会漂移，因为它描述的市场行为会发生变化。举个真实的例子：你编写了一个 30 日动量因子：

momentum_30 = close.pct_change(30).shift(1)

你期望：最近一个月涨幅较大的股票，未来还会涨。动量强 → 买入；动量弱 → 卖出。然后你在 2000–2010 年的美国市场上运行，效果很好。但一旦换到 2010–2020 年，动量收益减弱了。换到疫情时期（2020–2022），动量直接反向。这是因子漂移的本质：因子固化的是历史行为，市场结构变化时，你的特征就会失效。行为会变化：散户比例变化、高频交易兴起、ETF 的被动资金增加、政策环境变化、宏观经济状态变化。如果你将因子视为硬性规则，将是灾难性的。真正的理解应该是：因子不是“真理”，而是“假设”。假设随着市场变化随时可能失效。这就是它会漂移的根本原因。

三、为什么 99% 因子没用？

编写因子的过程类似于编写正则表达式：你想匹配“有规律的东西”，但你的数据本质上是噪声。你不断调整参数，只是使模型更“符合噪声”。最终，你得到了一个历史上表现极佳的因子。问题是：它不是抓住了规律，而是抓住了“当时的巧合”。为什么 99% 的因子无效？因为：你的窗口长度、平滑方法、标准化方式——全部是你随意选择的。金融市场主要是噪声。回测结果越好，越可能是过度拟合。你能想到的因子，别人早就已经测试过了。真正有效的因子很少，并且会被资本套利掉。最关键的是：因子的“有效性”不是公式，而是市场结构。市场结构不稳定，因此因子也不稳定。这就是为什么因子领域会让新手产生幻觉：你感觉因子很多，但实际上有效的极少。

四、动量因子实战（从构造 → 清洗 → 分组 → 验证）

我们将使用 yfinance 进行动量因子的完整实验。

Step 1：下载多只股票的数据

为了使因子能够比较不同股票的强弱，我们需要同时下载几只股票的数据。这里我选择了最常见的科技股：苹果、微软、亚马逊、谷歌、Meta。

import yfinance as yf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

tickers = ["AAPL", "MSFT", "AMZN", "GOOG", "META"]
data = yf.download(
tickers,
start="2015-01-01",
end="2023-01-01",
auto_adjust=True
)["Close"]
data.head()

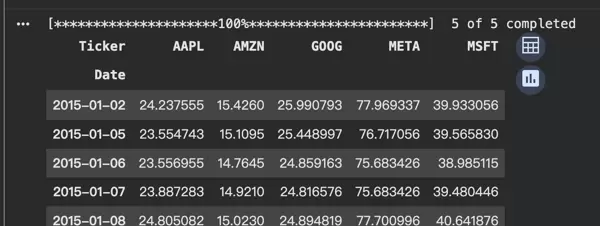
yfinance 将多只股票整合进同一个 DataFrame 中：
每一行代表一个交易日
每一列代表一只股票
单元格记录了当天的调整收盘价
这意味着，你获得的是一个“价格矩阵”。
接下来我们将对这个矩阵逐步实施特征工程。

步骤 2：构建 30 日动量因子（特征工程）
动量因子描述的是：“该股票在过去一个月内上涨了多少？”
这句话转化为代码即为：
过去 30 天的回报率
# 计算动量因子 基于获取的数据 计算过去30天的回报率 同时避免预知未来的数据
momentum = data.pct_change(30).shift(1)
其中

.shift(1)

是关键步骤。
若你不使用 shift，那么你在 1 月 5 日计算动量时，将会使用 1 月 5 日当天的收盘价。
然而你每天的交易决定只能基于“昨日及之前的数据”，
不能依赖“今日收盘后才能得知的数据”。
换句话说，

shift(1)

是将整个因子特征表“向后移动一天”，
确保：
每一行的因子仅包含当时实际可得的信息。
这一点至关重要，否则你的因子将“预见未来”，导致回测结果失真。

步骤 3：计算每日回报（用于评估分组表现）
现在我们有了因子，还需要每只股票每日的涨跌幅，
因为后续需要分析“动量强劲的股票组合”是否表现良好。
returns = data.pct_change()
这只是简单的单日回报率：
当日价格减去前一日价格，再除以前一日价格。

步骤 4：根据因子强度对每日股票进行分组
拥有动量因子后，我们需要了解它们在同一日内“相对强度”的排序。
为此，我们对每日的动量因子进行
百分位排名
按照动量因子的大小，将股票均匀划分为 3 组：
组 0：动量最弱
组 1：中间
组 2：动量最强
这是因子回测中最基本的方法，
目标是检验“强势组”是否持续更胜一筹。
rank_pct = momentum.rank(axis=1, pct=True)
groups = np.floor(rank_pct * 3).clip(0, 2)
groups = groups.fillna(1).astype(int)
此过程如下：

rank_pct

将每日所有股票按百分比排名（0~1）
乘以 3 后可得三个区间

floor

确保 0~0.33 归属第 0 组，0.33~0.66 归属第 1 组，依此类推

clip(0,2)

防止因 rank=1 而变为 3
最后填充缺失值并转换为整数
如此便获得了每日每只股票所在的“动量分组”。

步骤 5：计算每组的平均回报
现在我们有：
每只股票每日的回报（returns）
每只股票每日的分组（groups）
那么如何得出“强势股票组的回报曲线”？
方法很简单：
对属于这一组的股票的回报取平均。
group_returns = {
g: (returns * (groups == g)).mean(axis=1)
for g in [0, 1, 2]
}
这段代码非常巧妙：

(groups == g)

会形成一个 0/1 的掩码矩阵
与 returns 相乘后，属于该组的回报将被保留，不属于的则变为 0

.mean(axis=1)

从而得到该组当日的平均涨跌幅
这是量化研究中最典型的“等权重分组回测”。

步骤 6：绘制每个分组的累计回报曲线
当你将每日回报累积相乘后，即可获得每组的趋势曲线：
cum = pd.DataFrame(group_returns).add(1).cumprod()
cum.plot(figsize=(12,6))
plt.title("Momentum Factor – 3 Group Backtest")
plt.show()

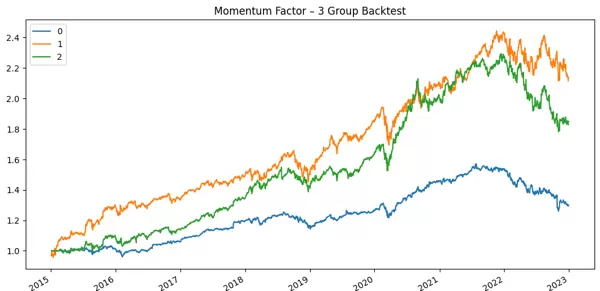
如果动量因子确实有效（显然这里的结果存在偏差），你应该看到以下情形：
动量最强组（2）整体表现最佳
动量最弱组（0）表现最差
中间组（1）介于两者之间
你刚才完成的这一整套流程，即是因子研究的基础框架：
构建一个特征 → 排序 → 分组 → 观察排序后的回报差异。
这比“观察图表”更为严谨，也能真正揭示：
“这个因子，在历史数据中是否具有解释力？”

RSI（Relative Strength Index，相对强弱指数）
RSI 是一个衡量“最近一段时间上涨还是下跌更多”的指标，数值范围通常在 0～100 之间。
直观上：
如果最近几天多数上涨，且下跌幅度较小 → RSI 会接近 70～80，通常被称为“超买”区间；
如果最近几天多数下跌，且上涨幅度较小 → RSI 会接近 20～30，通常被称为“超卖”区间。

传统 14 日 RSI 的计算步骤大致如下：

首先计算每日的价格变化：

\( \Delta P_t = P_t - P_{t-1} \)

\( \Delta P_t = P_t - P_{t-1} \)

如果 (\( \Delta P_t > 0 \))，则记录为“上升幅度（gain）”

如果 (\( \Delta P_t < 0 \))，则记录为“下降幅度（loss）”的绝对值

在一定周期内（例如 14 天），分别计算平均上升和平均下降：

\( \text{AvgGain} = \text{前14天所有升幅的平均值} \)

\( \text{AvgLoss} = \text{前14天所有降幅绝对值的平均值} \)

计算相对强度 RS（Relative Strength）：

\( RS = \frac{\text{AvgGain}}{\text{AvgLoss}} \)

最后将 RS 转换为 0～100 的 RSI：

\( RSI = 100 - \frac{100}{1 + RS} \)

解析：

当 \( AvgGain > AvgLoss \)（近期上升多于下降）时，RS 较高，RSI 接近 100；

当 \( AvgLoss > AvgGain \)（近期下降多于上升）时，RS 较低，RSI 接近 0；

交易软件中常见的应用：

\( RSI > 70 \)：许多人认为“超买”，可能存在回调风险；

\( RSI < 30 \)：许多人认为“超卖”，可能存在反弹机会。

然而这些只是经验法则，不是自然定律，更非“必然涨跌”的信号。

MACD（Moving Average Convergence Divergence，指数平滑异同移动平均线）

MACD 是一个基于移动平均线的趋势指标，用于描述“短期价格走势”与“长期价格走势”之间的差异。

简单来说：

当短期价格显著高于长期趋势 → MACD 为正值，通常被视为“看涨”；

当短期价格显著低于长期趋势 → MACD 为负值，通常被视为“看跌”。

标准 MACD（12, 26, 9）的传统计算步骤：

计算两个不同周期的指数移动平均线（EMA）：

快速线 EMA(fast)：通常使用 12 日 EMA

慢速线 EMA(slow)：通常使用 26 日 EMA

EMA 的公式类似：

\( EMA_t = \alpha \cdot P_t + (1 - \alpha) \cdot EMA_{t-1} \)

其中 (\( \alpha = \frac{2}{N+1} \))，N 为周期长度（如 12 或 26）。

计算两条 EMA 的差值，称为 DIF（部分资料直接称为 MACD 线）：

\( DIF_t = EMA_{\text{fast}, t} - EMA_{\text{slow}, t} \)

若 DIF > 0，表示短期价格高于长期均线，且相对较强；

若 DIF < 0，表示短期价格低于长期均线，且相对较弱。

再对 DIF 进行一次平滑处理，得出“信号线”（DEA 或 signal line）：

通常使用 9 日 EMA：

\( DEA_t = EMA_9(DIF_t) \)

某些软件还会绘制一条柱状图：

\( \text{MACD histogram} = DIF_t - DEA_t \)

直观理解：

DIF 表示“短期趋势 - 长期趋势”；

DEA 表示“DIF 的平滑版本”；

当 DIF 从下方穿过 DEA 时，许多人将其视为买入信号；

当 DIF 从上方穿破 DEA 时，许多人将其视为卖出信号。

这种用法在技术分析中非常普遍，但本质上：

RSI、MACD 都是对价格“进行变换”的一种数学处理方式；

它们可以作为“技术指标”使用，也可以作为“特征/因子”的一部分；

但它们仅是对历史价格动态的某种压缩与描述。