复变函数：傅里叶变换的性质 [推广有奖]

傅里叶变换核心性质的直观理解与记忆方法

在学习信号与系统过程中，傅里叶变换的各种性质常常让人感到公式繁杂、难以记忆。面对一连串数学表达式，若缺乏物理直觉支撑，很容易陷入死记硬背的困境。本文将从生活化类比出发，借助果汁勾兑、音乐播放、调频广播等实际场景，帮助你建立对傅里叶变换五大核心性质的深层理解，并实现高效记忆。

在进入具体性质之前，先建立一个关键认知：傅里叶变换本质上是一种“频率成分检测器”，它把任意信号（无论周期与否）分解为不同频率的复指数分量；而逆变换则是根据这些频率信息重新合成原始信号。两者互为逆操作，如同分析与重构的过程。

1. 线性性质（又称“勾兑性”）

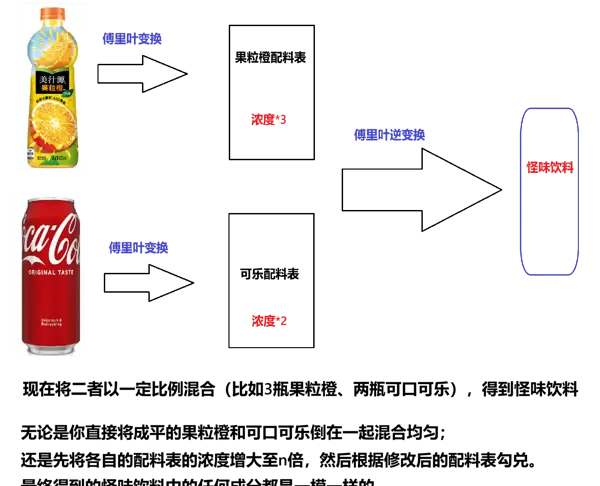
设想你手边有两杯饮料：一杯是果粒橙，记作 f(t)；另一杯是可口可乐，记作 f(t)。现在你想调配出一种新饮品，比如按比例混合这两者，得到 a·f(t) + b·f(t)。

此时，傅里叶变换就像一台“成分配方提取机”——它可以将任何饮料转化为对应的粉末配方（即频域表示）。而逆变换则相当于用这份配方还原成饮料。

线性性质告诉我们：无论是先混合饮料再提取配方，还是先分别提取配方再按比例混合粉末，最终得到的结果是一样的。也就是说，变换与线性组合可以交换顺序：

[a·f(t) + b·f(t)] = a·F(ω) + b·F(ω)

这一性质在简化复杂信号处理时非常有用，也体现了系统的可叠加性。

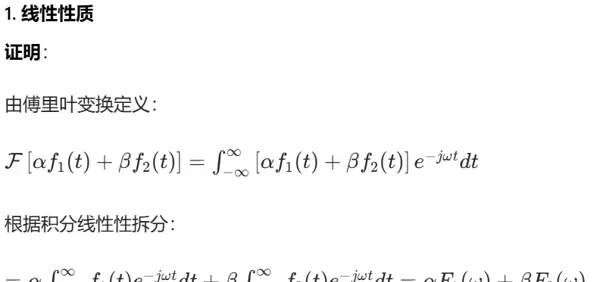
2. 伸缩性质

考虑一段音频信号 f(t)，例如一首歌曲。当你以2倍速播放这首歌时，相当于构造了一个新的函数 f(2t)，时间被压缩了一半。

这时你会明显感觉到两个变化：

• 音调变高：所有声音变得更尖细，男声像卡通人物。这是因为每个频率成分都被放大了两倍——原本440Hz的小提琴变成了880Hz。
• 整体音量不变：虽然高频带来更强的能量感，但播放时间缩短一半，总能量保持守恒。

从数学角度看，若原信号的基频为 W，周期为 T，则压缩后周期变为 T/2，频率变为 2W。为了维持能量一致，在频域中需要引入一个幅度衰减因子 1/2。

因此，伸缩性质表明：时间尺度越小（快放），频率范围越宽，且各频率幅值相应缩小。

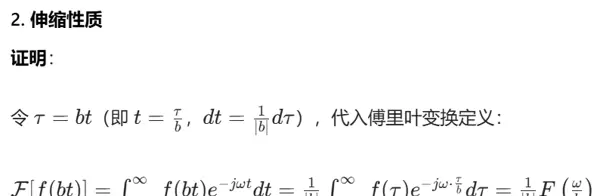
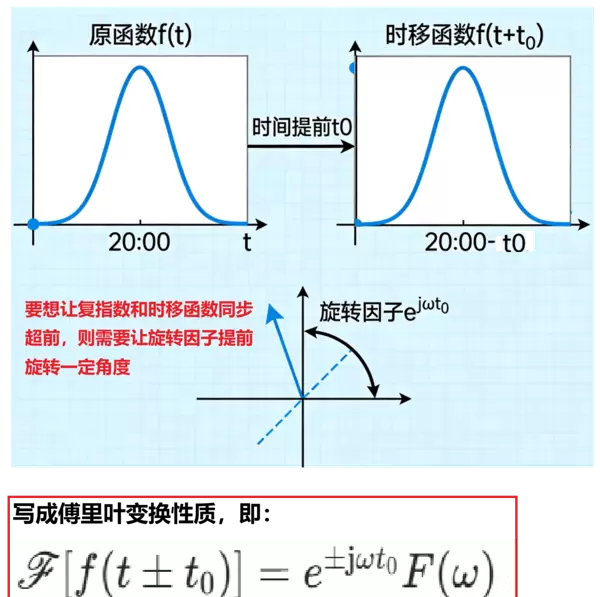
3. 时移性质

任何信号都可以看作多个正弦和余弦波的叠加。假设一段音乐原定晚上8点开始播放，现在提前 t 时间开始，即信号变为 f(t + t)。

这种时间上的平移，在三角函数中体现为相位的变化。通过欧拉公式 e^(jωt) = cos(ωt) + j·sin(ωt)，我们可以将正余弦表示为复平面上的旋转矢量。

当时间提前 t，相当于该矢量在初始时刻就多转过了 ωt 的角度，也就是乘上了 e^(jωt) 这个旋转因子。由于是提前播放（左移），对应正相位偏移，故频域结果整体乘以 e^(jωt)。

总结来说：信号在时域中的延迟或提前，会在频域中表现为各频率成分的相位旋转，且旋转角度与频率和时移量成正比。

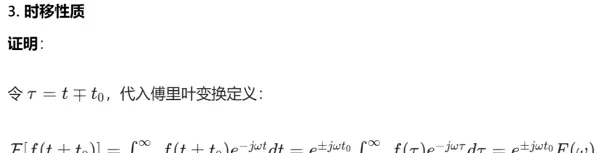
4. 频移性质

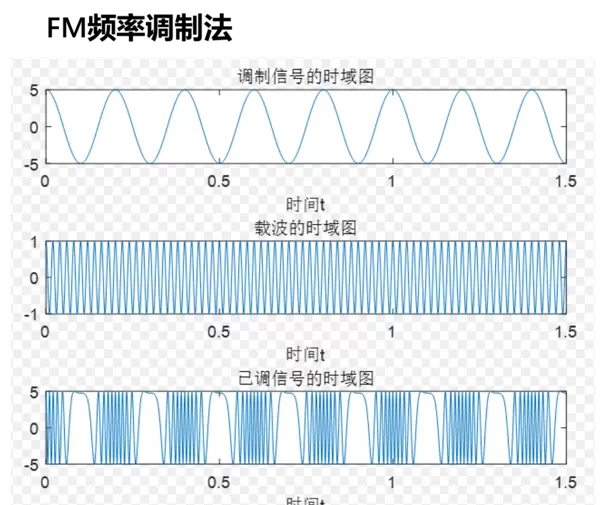
频移性质在通信系统中有重要应用，尤其体现在调制技术中。低频信号（如语音）无法远距离传输，因此需要将其“搬移”到高频段，便于发射。

这个过程称为调制：用一个高频载波（如 cos(ωt)）去乘以原始信号 f(t)。利用欧拉公式，cos(ωt) 可表示为 [e^(jωt) + e^(-jωt)] / 2，因此在傅里叶变换中，我们常用 e^(jωt) 来代表载波作用。

当 f(t) 乘上 e^(jωt) 后进行傅里叶变换，其频谱会整体向右移动 ω，即从 F(ω) 变为 F(ω - ω)。这里要注意函数平移规则：“左加右减”导致符号相反。

接收端只需反向操作（解调）并滤除高频部分，即可恢复原始信号。这就是无线电广播的基本原理。

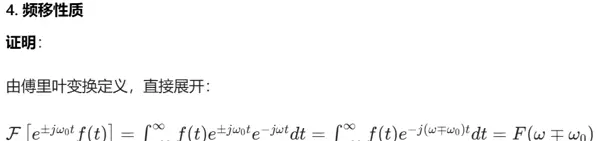
5. 微分与积分性质

对于微分和积分性质，虽较难找到完全贴切的生活类比，但仍可通过数学本质辅助记忆。

基本结论如下：

• 信号求导后的傅里叶变换等于原频谱乘以 jω；
• 信号积分后的变换等于原频谱除以 jω（前提是直流分量为零）。

为什么是 jω？可以从复指数信号 e^(jωt) 入手：

对其求导得 d/dt [e^(jωt)] = jω·e^(jωt)，说明高频信号变化率更大，响应更强。这正是高通滤波的特性——微分增强高频、抑制低频。

反之，积分是对过去值的累加，起到平滑作用，削弱快速波动成分，体现出低通滤波效果。

因此，微分性质关联高频增强，积分性质关联低频保留，系数 jω 成为连接时域变化与频域响应的关键桥梁。

积分的本质是累加求和。在极短时间内的采样过程中，高频信号由于正负波动更为频繁，导致其在累加过程中相互抵消的程度更大。因此，积分运算对高频成分具有抑制作用，而对低频成分则更容易保留和通过。