通过某一变换函数,对原有图像中的每个像素值进行转换,得到新的像素值来构成新的图像。这一变换操作是针对图像中每个像素点进行,故称为“点运算”。今天给大家讲解数字图像处理方法入门——灰度图像的点运算
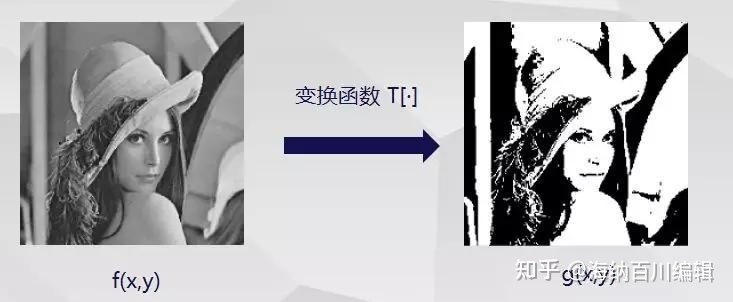
01
灰度直方图
一、灰度直方图的数学定义:
展示图像中各个灰度值出现的次数的二维统计图表
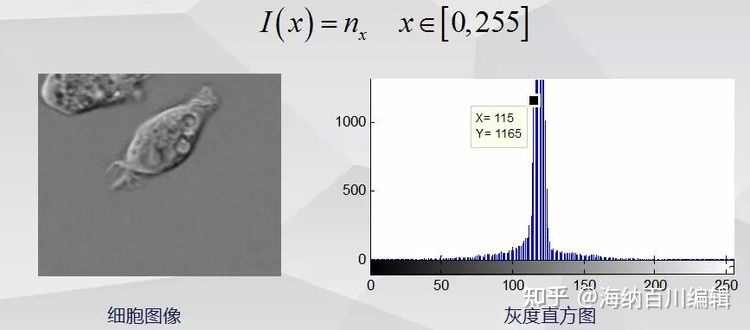
程序实例:基于细胞图像,获取其灰度直方图

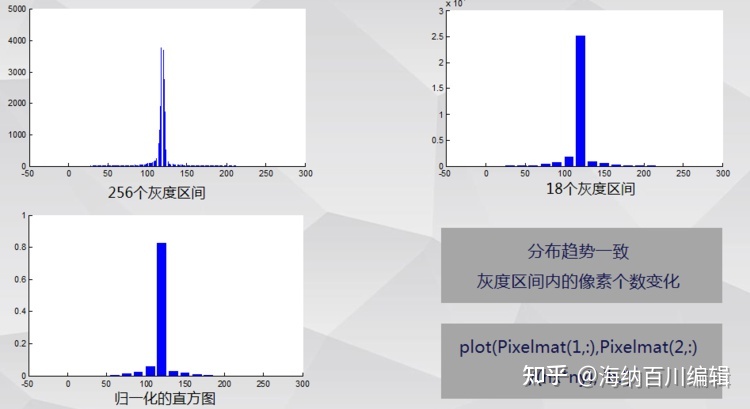
二、MATLAB自带直方图生成命令与自定义程序的结果对比:
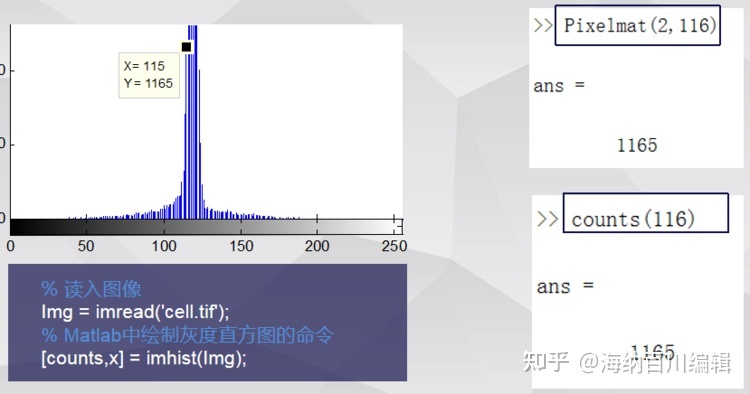
程序实例:自定义的划分灰度直方图的区间
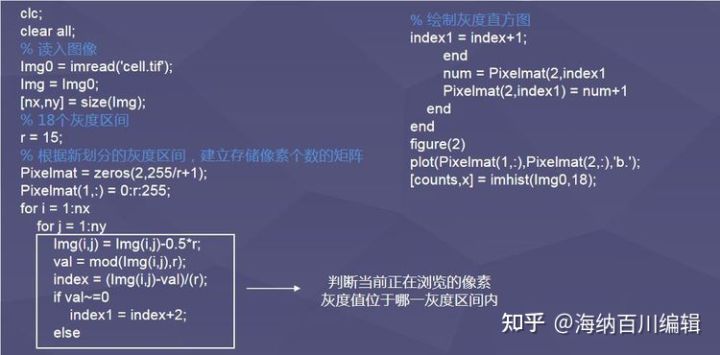
不同数量的灰度区间内,直方图的分布形式
02
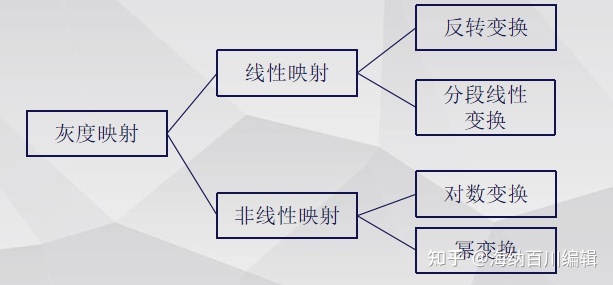
常用的点运算函数
灰度图像的点运算实质上等同于图像的灰度映射,是若干以改变图像对比度,图像灰度值为目标的操作。
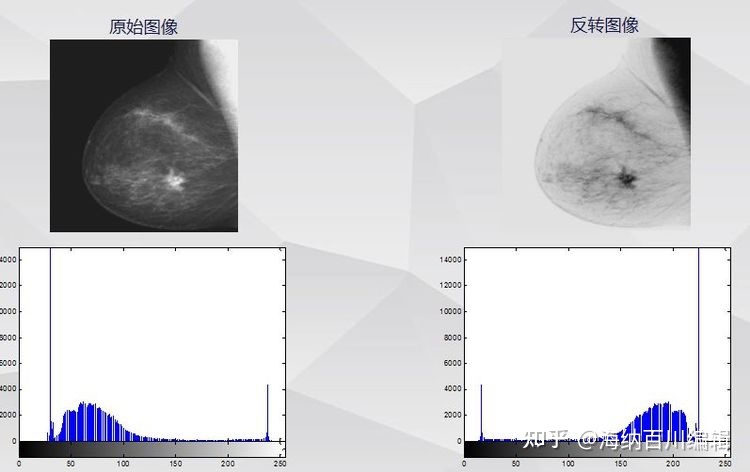
一、反转变换的定义与程序实例
反转变换:假定图像灰度级为[0, L-1],原始图像的灰度值存储于矩阵F中,变换后图像的灰度值存储于矩阵S中,则将灰度级的最大灰度值(L-1)减去原有图像的灰度值,即得到反转图像。
变换函数:S = L-1-F

反转变换前后的图像及直方图分布:
二、分段线性函数的定义与程序实例
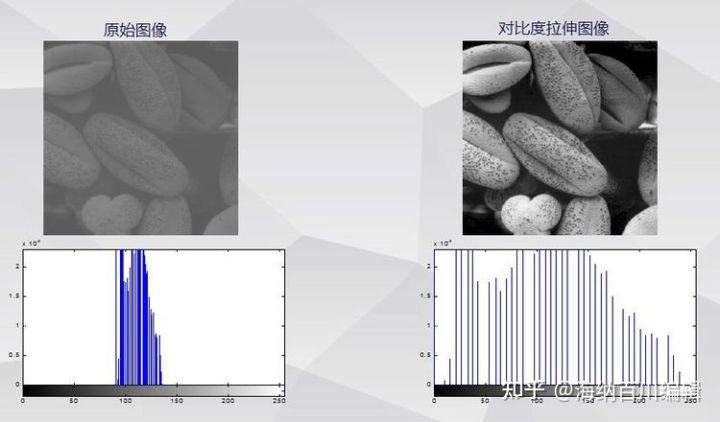
分段线性变换:对比度拉伸
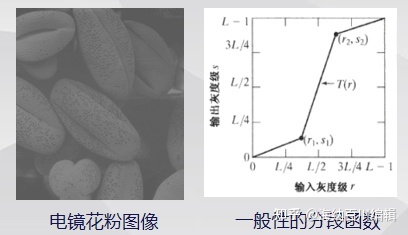
用户通过设定线性的分段函数,扩大图像的动态灰度范围,从而达到提升图像对比度的效果。

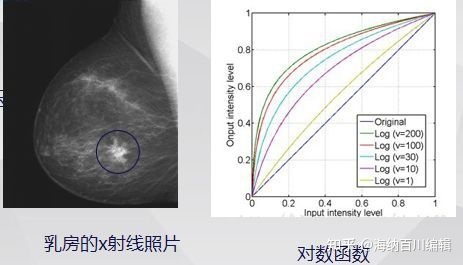
三、对数/反对数变换的定义与程序实例
通过对数/反对数函数,实现图像灰度动态范围的扩展与压缩。
S = b*log(1+F)

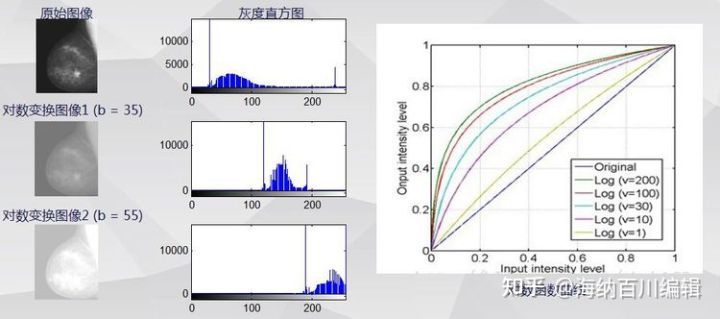
不同变换系数下的对数变换结果和直方图展示
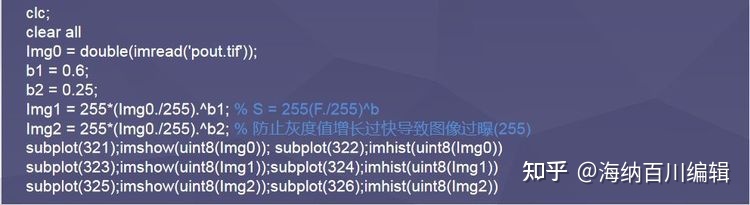
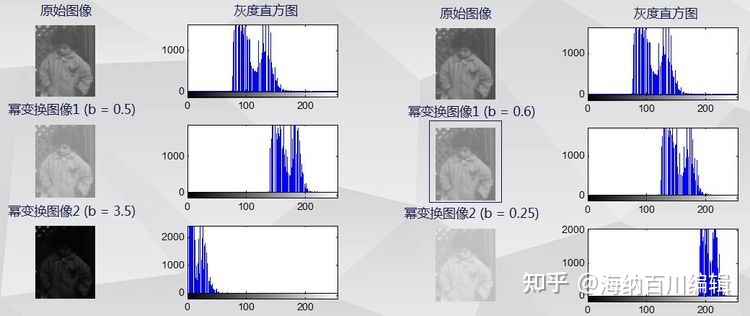
四、幂变换的定义与程序实例
通过幂函数,实现图像灰度动态范围的扩展与压缩。b>1时效果与对数变换一致;0

不同变换系数下的幂变换结果和直方图展示:
03
灰度直方图均衡化
一、灰度直方图均衡化的定义:
基于人眼对灰度差别越大的像素越容易分辨的原理。扩展原始图像的灰度动态范围,使得一定灰度范围内的像素数量大致相同,即达到灰度分布的“均衡”,实现图像增强。
S = T(F)

连续情况下的灰度直方图均衡化的推导:

二、离散情况下的灰度直方图均衡化的推导:
设一副图像的像素总个数为n,该图像具有L级灰度,则nk代表灰度级为fk的像素个数。则灰度级为fk出现的概率(概率密度函数)p(fk)为:

连续情况下的累积分布函数T中的积分部分,在离散情况下,将变为求和的形式:

灰度直方图均衡化的形象化推导
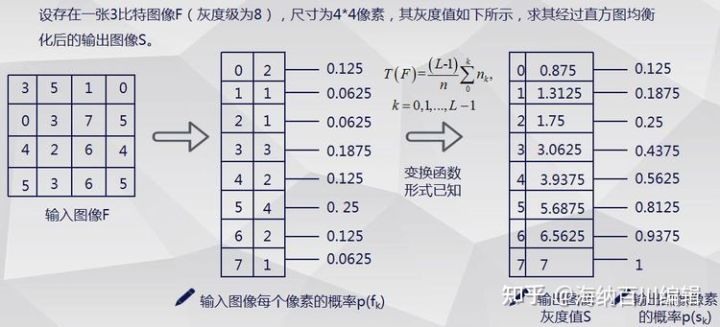
程序实例:对花粉图像进行灰度直方图均衡化

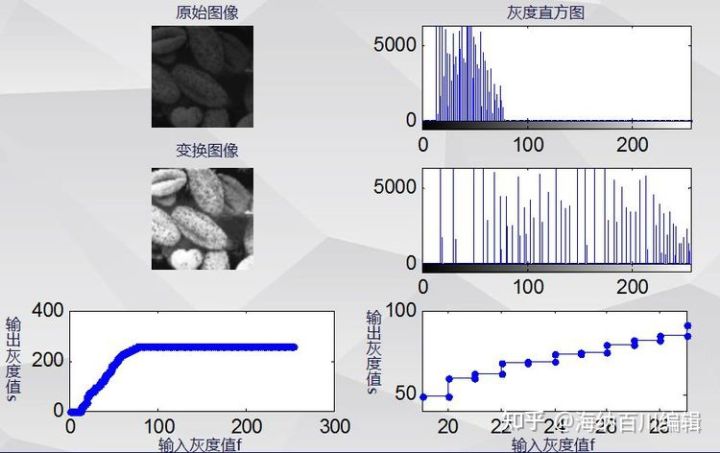
灰度直方图均衡化针对花粉图像的处理效果:
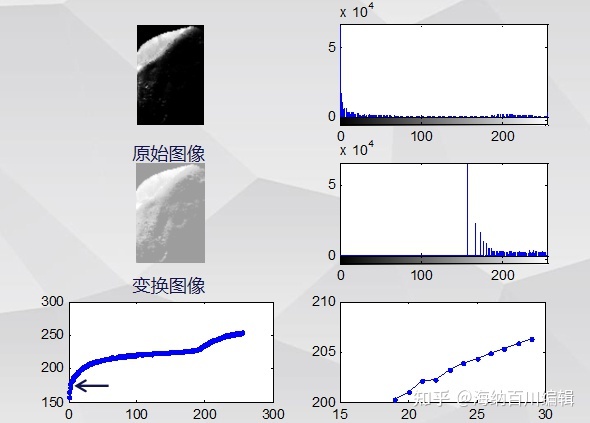
三、灰度直方图均衡化存在的缺陷:
由于直方图均衡化得到的输出图像概率密度函数是确定的均匀分布,导致直方图均衡化成为一个自动的图像增强过程。它并不能满足所有图像。
04
灰度直方图规定化
灰度直方图规定化的定义和关键数学公式:
设p(f)是输入图像灰度分布的概率密度函数, p(z)是规定的输出图像具备的概率密度函数, p(s)是直方图均衡化后输出图像的概率密度函数:
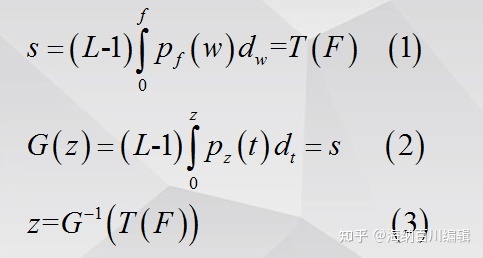
对于同一图像,无论输入的概率密度函数有何变化( p(f) 和p(z) 不同),经过直方图均衡化后,输出的概率密度函数是相同的均匀分布
关键:求得到规定概率密度p(z)的规定输出图像Z
已知条件:
1、设一副图像的像素总个数为n,该图像具有L级灰度,则nk代表灰度级为fk的像素个数。则灰度级为fk出现的概率(概率密度函数)p(fk)=fk/n;2、规定的灰度直方图里, nz代表灰度级为fz的像素个数。则灰度级为fz出现的概率(概率密度函数)p(fz)=nz/n
待求:规定概率密度p(z)的规定输出图像Z

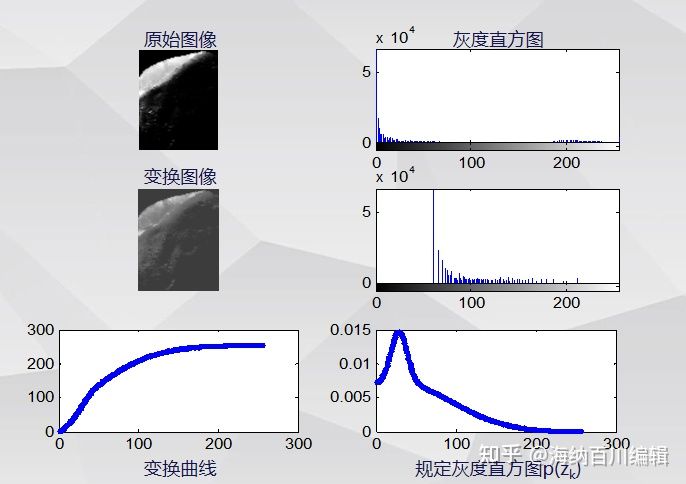
程序实例:对月球图像进行灰度直方图规定化(1)

程序实例:对月球图像进行灰度直方图规定化(2)

灰度直方图规定化对月球图像的处理效果:




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







