1991-2022年月度的日平均特质波动率和特质偏度（stata计算）

相似文件 换一批

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

1.计算说明
首先进行如下式的Fama-French三因子回归

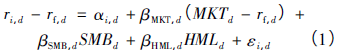
其中：
d∈S（t）
ri,d是股票i在第d日的收益率（考虑现金红利再投资的日个股回报率）
rf,d是第d日的无风险利率
MKTd、SMBd和HMLd分别是第d日的市场投资组合收益率（考虑现金红利再投资的综合日市场回报率流通市值加权平均法）、基于公司规模的投资组合收益率和基于账面市值比的投资组合收益率
βMKT,d、βSMB,d和βHML,d分别是股票收益率对市场投资组合、基于公司规模的投资组合和基于账面市值比的投资组合这3个因素的敏感度，也就是本文所说的回归系数
αi,d是股票i在第d日的回归常数项
εi,d是股票i在第d日的回归残差项

已实现的特质波动率IVi,t，和特质偏度ISi,t分别按照下面式（2）和式（3）计算

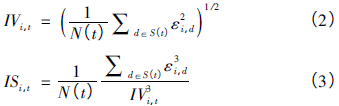
由上两式计算出月度的日平均特质波动率和特质偏度。
注：如果正常交易的交易日数目不足这个月总交易日天数的80%，该股票在这个月将不会纳入研究范畴。

2.数据说明
样本选择：全部A股1991-2022年数据（初始数据是从1990年开始，经过处理后的数据起点为1991年）
对最终结果进行了1%和99%分位数的缩尾处理
每个压缩包都附有初始数据，计算代码，参考文献和最终数据

3.参考文献
[1]郑振龙,王磊,王路跖.特质偏度是否被定价?[J].管理科学学报,2013,16(05):1-12.
[2]熊和平,刘京军,杨伊君,周靖明.中国股票市场存在特质波动率之谜吗?——基于分位数回归模型的实证分析[J].管理科学学报,2018,21(12):37-53.

压缩包所含文件：


数据样例：


分年份数据量统计：


缩尾后的描述性统计结果：


特质波动率和特质偏度.rar (98.72 MB, 需要: RMB 39 元) 本附件包括：

• 计算代码.do
• 计算结果.dta
• 日个股回报率文件1990-20230217.dta
• 三因子模型指标日.dta
• 无风险利率文件.dta
• 综合日市场回报率文件1990-20230217.dta
• 计算结果.xlsx
• 特质偏度是否被定价__郑振龙.pdf
• 中国股票市场存在特质波动率...于分位数回归模型的实证分析_熊和平.pdf

2023-2-19 18:35:00 上传

2022
需要: RMB 39 元  [购买]

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏1 回帖

关键词：Stata tata 波动率 日平均 分位数回归模型

您好，这个是不是下载下来改好文件路径就好啦

lxr的猫 发表于 2023-6-2 17:02
您好，这个是不是下载下来改好文件路径就好啦

您好，是的

您好，我刚刚购买了这个，我还想咨询您关于彩票型股票识别体系stata的购买