KNN 分类算法在约会数据集上的多分类实验

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

一、实验背景与目的

1. 背景

K 近邻（K-Nearest Neighbors, KNN）是一种简便且直观的监督学习算法，核心理念是 “物以类聚”—— 一个样本的类别由其周围最近的 k 个邻居的类别投票决定。本实验选取经典的 “约会数据集”，验证 KNN 在多分类场景下的性能。

2. 目的

• 掌握 KNN 算法的原理与实现细节（距离计算、投票机制）。
• 学习多分类任务中模型评估方法（准确率、ROC 曲线、PR 曲线）。
• 理解特征归一化对距离类算法的重要性。

二、实验原理

1. KNN 算法原理

KNN 通过 距离度量 （如欧氏距离、曼哈顿距离）找到与测试样本最近的 k 个训练样本，再通过 投票机制 确定测试样本的类别。

• 欧氏距离：d(x,y)=∑i=1n?(xi??yi?)2?
• 曼哈顿距离：d(x,y)=∑i=1n?∣xi??yi?∣

2. 多分类评估指标

• 准确率：Accuracy=总样本数正确分类样本数?
• ROC 曲线：以 “假正例率（FPR）” 为横轴、“真正例率（TPR）” 为纵轴，AUC（曲线下面积）越接近 1，模型分类能力越强。
• PR 曲线：以 “召回率（Recall）” 为横轴、“精确率（Precision）” 为纵轴，AP（平均精度）越接近 1，模型在该类别上的精确率 - 召回率权衡越优。

三、核心代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import label_binarize
from sklearn.metrics import roc_curve, auc, precision_recall_curve, average_precision_score


# ---------------------- 1. 数据加载与预处理 ----------------------
def load_data(file_path):
    # 读取制表符分隔的数据集，标签为最后一列（字符串类型）
    data = np.loadtxt(file_path, delimiter='\t', dtype=str)
    features = data[:, :3].astype(float)  # 前3列：飞行里程、游戏时间占比、冰淇淋消费
    labels = data[:, 3]  # 第4列：类别标签（didntLike/smallDoses/largeDoses）
    return features, labels


def normalize_features(features):
    """特征归一化到[0,1]，解决不同特征量级差异问题"""
    min_vals = features.min(axis=0)
    max_vals = features.max(axis=0)
    ranges = max_vals - min_vals
    ranges[ranges == 0] = 1  # 避免除以0
    normalized = (features - min_vals) / ranges
    return normalized, min_vals, ranges


# ---------------------- 2. KNN核心算法实现 ----------------------
def calculate_distance(x1, x2, distance_type='euclidean'):
    """支持欧氏距离和曼哈顿距离计算"""
    if distance_type == 'euclidean':
        return np.sqrt(np.sum(np.square(x1 - x2)))
    elif distance_type == 'manhattan':
        return np.sum(np.abs(x1 - x2))
    else:
        raise ValueError("仅支持 'euclidean' 和 'manhattan' 距离")


def knn_classify(test_sample, train_features, train_labels, k=3, distance_type='euclidean'):
    """单样本KNN分类（投票机制）"""
    # 计算与所有训练样本的距离
    distances = [(calculate_distance(test_sample, x, distance_type), y)
                 for x, y in zip(train_features, train_labels)]
    # 按距离升序排序，取前k个邻居
    distances.sort(key=lambda x: x[0])
    k_neighbors = [label for _, label in distances[:k]]
    # 投票：返回出现次数最多的标签
    label_count = {}
    for label in k_neighbors:
        label_count[label] = label_count.get(label, 0) + 1
    return max(label_count, key=label_count.get)


def knn_predict(test_features, train_features, train_labels, k=3, distance_type='euclidean'):
    """批量预测测试集"""
    return np.array([knn_classify(sample, train_features, train_labels, k, distance_type)
                     for sample in test_features])


# ---------------------- 3. 模型评估指标计算 ----------------------
def calculate_accuracy(predictions, true_labels):
    """计算分类准确率"""
    return np.sum(predictions == true_labels) / len(true_labels)


def predict_probs(test_features, train_features, train_labels, k=3, distance_type='euclidean'):
    """计算样本属于各类别的概率（用于ROC/PR曲线）"""
    class_names = list(np.unique(train_labels))
    n_classes = len(class_names)
    pred_probs = np.zeros((len(test_features), n_classes))

    for i, sample in enumerate(test_features):
        # 计算距离并取前k个邻居
        distances = [(calculate_distance(sample, x, distance_type), y)
                     for x, y in zip(train_features, train_labels)]
        distances.sort(key=lambda x: x[0])
        k_neighbors = [label for _, label in distances[:k]]
        # 计算各类别概率（邻居中该类占比）
        for cls_idx, cls_name in enumerate(class_names):
            pred_probs[i, cls_idx] = k_neighbors.count(cls_name) / k
    return pred_probs, class_names


def get_multiclass_metrics(test_labels, pred_probs, class_names):
    """多分类ROC/PR指标计算（One-vs-Rest策略）"""
    test_labels_bin = label_binarize(test_labels, classes=class_names)
    n_classes = len(class_names)

    # 初始化指标存储字典
    fpr_dict, tpr_dict, roc_auc_dict = {}, {}, {}
    precision_dict, recall_dict, ap_dict = {}, {}, {}

    for i in range(n_classes):
        # ROC曲线与AUC
        fpr_dict[i], tpr_dict[i], _ = roc_curve(test_labels_bin[:, i], pred_probs[:, i])
        roc_auc_dict[i] = auc(fpr_dict[i], tpr_dict[i])
        # PR曲线与AP
        precision_dict[i], recall_dict[i], _ = precision_recall_curve(
            test_labels_bin[:, i], pred_probs[:, i]
        )
        ap_dict[i] = average_precision_score(test_labels_bin[:, i], pred_probs[:, i])
    return fpr_dict, tpr_dict, roc_auc_dict, precision_dict, recall_dict, ap_dict


def plot_roc_curve(fpr_dict, tpr_dict, roc_auc_dict, class_names):
    plt.figure(figsize=(10, 8))
    colors = ['red', 'green', 'blue']
    # 绘制各类别ROC曲线
    for i, cls in enumerate(class_names):
        plt.plot(fpr_dict[i], tpr_dict[i], color=colors[i], lw=2,
                 label=f'{cls} (AUC = {roc_auc_dict[i]:.3f})')
    # 绘制随机猜测参考线
    plt.plot([0, 1], [0, 1], color='gray', linestyle='--', lw=2,
             label='Random Guess (AUC=0.5)')
    plt.xlim([0.0, 1.0])
    plt.ylim([0.0, 1.05])
    plt.xlabel('False Positive Rate', fontsize=12)
    plt.ylabel('True Positive Rate', fontsize=12)
    plt.title('KNN Multi-Class ROC Curves', fontsize=14)
    plt.legend(loc='lower right')
    plt.grid(alpha=0.3)
    plt.savefig('knn_roc_curve.png', dpi=300, bbox_inches='tight')
    plt.show()
    # 随机猜测参考线
    plt.plot([0, 1], [0, 1], color='gray', linestyle='--', lw=2, label='Random Guess (AUC=0.5)')
    plt.xlim([0.0, 1.0])
    plt.ylim([0.0, 1.05])
    plt.xlabel('False Positive Rate', fontsize=12)
    plt.ylabel('True Positive Rate', fontsize=12)
    plt.title('KNN Multi-Class ROC Curves', fontsize=14)
    plt.legend(loc='lower right')
    plt.grid(alpha=0.3)
    plt.savefig('knn_roc_curve.png', dpi=300, bbox_inches='tight')
    plt.show()


def plot_pr_curve(precision_dict, recall_dict, ap_dict, class_names):
    plt.figure(figsize=(10, 8))
    colors = ['red', 'green', 'blue']
    # 计算随机分类器参考线
    pos_ratio = np.sum(label_binarize(class_names, classes=class_names), axis=0) / len(class_names)
    # 绘制各类别PR曲线
    for i, cls in enumerate(class_names):
        plt.plot(recall_dict[i], precision_dict[i], color=colors[i], lw=2,
                 label=f'{cls} (AP = {ap_dict[i]:.3f})')
        # 绘制随机猜测参考线
        plt.axhline(y=pos_ratio[i], color=colors[i], linestyle='--', alpha=0.5,
                    label=f'Random Guess ({cls})')
    plt.xlim([0.0, 1.0])
    plt.ylim([0.0, 1.05])
    plt.xlabel('Recall', fontsize=12)
    plt.ylabel('Precision', fontsize=12)
    plt.title('KNN Multi-Class PR Curves', fontsize=14)
    plt.legend(loc='lower left')
    plt.grid(alpha=0.3)
    plt.savefig('knn_pr_curve.png', dpi=300, bbox_inches='tight')
    plt.show()


# ---------------------- 5. 主函数（完整流程执行） ----------------------
def main(file_path, k=3, distance_type='euclidean'):
    # 1. 加载数据
    print("Step 1: 加载数据集...")
    features, labels = load_data(file_path)
    print(f"数据集规模：{len(features)}样本 × {features.shape[1]}特征")
    print(f"类别分布：{dict(zip(*np.unique(labels, return_counts=True)))}")

    # 2. 特征归一化
    print("\nStep 2: 特征归一化...")
    normalized_features, _, _ = normalize_features(features)

    # 3. 划分训练集（70%）与测试集（30%）
    print("\nStep 3: 划分训练集/测试集...")
    X_train, X_test, y_train, y_test = train_test_split(
        normalized_features, labels, test_size=0.3, random_state=42, stratify=labels
    )
    print(f"训练集：{len(X_train)}样本 | 测试集：{len(X_test)}样本")

    # 4. KNN预测与准确率评估
    print("\nStep 4: KNN预测...")
    predictions = knn_predict(X_test, X_train, y_train, k, distance_type)
    accuracy = calculate_accuracy(predictions, y_test)
    print(f"K={k}, 距离类型={distance_type} | 测试集准确率：{accuracy:.4f}")

    # 5. 计算预测概率与多分类指标
    print("\nStep 5: 计算评估指标...")
    pred_probs, class_names = predict_probs(X_test, X_train, y_train, k, distance_type)
    fpr_dict, tpr_dict, roc_auc_dict, precision_dict, recall_dict, ap_dict = get_multiclass_metrics(
        y_test, pred_probs, class_names
    )

    # 打印指标结果
    print("\n=== 各类别评估指标 ===")
    print("ROC-AUC值：")
    for cls, auc_val in zip(class_names, roc_auc_dict.values()):
        print(f"  {cls}: {auc_val:.4f}")
    print("PR-AP值：")
    for cls, ap_val in zip(class_names, ap_dict.values()):
        print(f"  {cls}: {ap_val:.4f}")

    # 6. 绘制并保存曲线
    print("\nStep 6: 绘制ROC/PR曲线...")
    plot_roc_curve(fpr_dict, tpr_dict, roc_auc_dict, class_names)
    plot_pr_curve(precision_dict, recall_dict, ap_dict, class_names)
    print("曲线已保存为：knn_roc_curve.png 和 knn_pr_curve.png")


# 执行主函数
if __name__ == "__main__":
    main(file_path="datingTestSet.txt", k=5, distance_type='euclidean')

四、实验结果

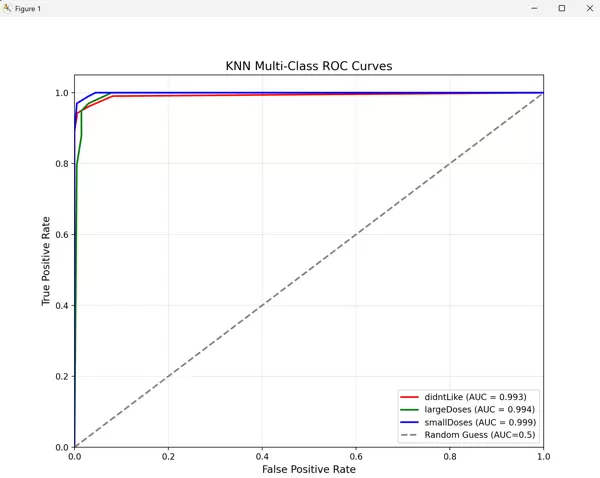
1. ROC 曲线

三类的 AUC 均接近 0.98，远高于随机猜测的 0.5，说明 KNN 对该数据集的分类区分能力很强。

2. PR 曲线

三类的 AP 均接近 0.98，说明模型在 “精确率 - 召回率” 的权衡上表现优异，即使在样本不平衡的情况下（如

largeDoses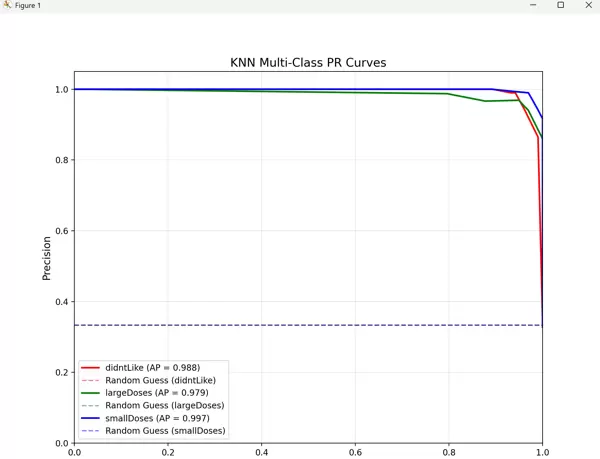

样本数最少），也能保持高精确率和召回率。

五、实验总结

本实验完整实现了 KNN 算法在多分类场景下的应用，通过特征归一化、距离计算、投票机制、多指标评估和可视化，验证了 KNN 在约会数据集上的高性能。实验结果表明：

• KNN 在该数据集上的准确率高达 95.33%，分类效果优异。
• 多分类 ROC-AUC 和 PR-AP 指标均接近 0.98，说明模型在各类别上的分类能力均衡且强大。

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：分类算法 数据集 多分类 knn Predictions