引言:决策树为何成为机器学习入门首选?
决策树是机器学习中最容易理解的算法之一,它通过模拟类似 "if-else" 的分支逻辑实现分类任务,不仅具有较强的可解释性,还能同时处理分类与回归问题。本文将以贷款审批数据集为例,从零构建两种经典决策树 —— 基于信息增益的 ID3 算法和基于基尼系数的 CART 算法,并通过实践对比它们的分裂逻辑与性能差异。
一、数据集介绍:贷款审批数据
我们使用的数据集包含 16 条贷款申请人信息,特征包括 "年龄段"、"有工作"、"有自己的房子" 和 "信贷情况",目标是预测 "是否给贷款"。数据集结构如下:
data = {
"年龄段": ["青年","青年","青年","青年","青年","中年","中年","中年","中年","中年","老年","老年","老年","老年","老年","老年"],
"有工作": ["否","否","是","是","否","否","否","是","否","否","否","否","是","是","否","否"],
"有自己的房子": ["否","否","否","是","否","否","否","是","是","是","是","是","否","否","否","否"],
"信贷情况": ["一般","好","好","一般","一般","一般","好","好","非常好","非常好","非常好","好","好","非常好","一般","非常好"],
"类别(是否给贷款)": ["否","否","是","是","否","否","否","是","是","是","是","是","是","是","否","否"]
}该数据集的特点是:所有特征均为离散型,目标变量为二分类(是 / 否),非常适合决策树算法的处理。
二、ID3 决策树:基于信息增益的分裂逻辑
ID3 算法是决策树的经典实现,其核心思想是选择信息增益最大的特征作为分裂节点,通过减少数据集的 "混乱程度"(熵)来实现分类。
1. ID3 核心公式实现
- 信息熵(衡量数据集混乱程度)
熵越高,数据类别越混杂:
def calculate_entropy(y): class_counts = {} for label in y: class_counts[label] = class_counts.get(label, 0) + 1 entropy = 0.0 total = len(y) for count in class_counts.values(): p = count / total entropy -= p * math.log2(p) if p != 0 else 0 return entropy - 信息增益(特征分裂的效果)
信息增益 = 分裂前的熵 - 分裂后的加权熵,值越大说明特征分类效果越好:
def calculate_information_gain(X, y, feature): total_entropy = calculate_entropy(y) feature_values = X[feature].unique() weighted_entropy = 0.0 total_samples = len(y) for value in feature_values: mask = X[feature] == value subset_y = y[mask] subset_size = len(subset_y) weighted_entropy += (subset_size / total_samples) * calculate_entropy(subset_y) return total_entropy - weighted_entropy
2. ID3 决策树的构建与可视化
通过递归选择信息增益最大的特征,逐步分裂节点,最终构建完整的决策树:
def build_id3_tree(X, y, features, depth=0, max_depth=3):
# 终止条件:所有样本类别相同或达到最大深度
if len(set(y)) == 1:
return {"type": "leaf", "class": y.iloc[0]}
if len(features) == 0 or depth >= max_depth:
return {"type": "leaf", "class": majority_vote(y)}
# 选择最佳分裂特征
best_feature, best_gain = choose_best_feature_id3(X, y)
tree = {
"type": "node", "feature": best_feature, "gain": best_gain, "children": {}
}
# 递归构建子树
remaining_features = [f for f in features if f != best_feature]
for value in X[best_feature].unique():
mask = X[best_feature] == value
subset_X = X[mask]
subset_y = y[mask]
tree["children"][value] = build_id3_tree(
subset_X, subset_y, remaining_features, depth + 1, max_depth
)
return tree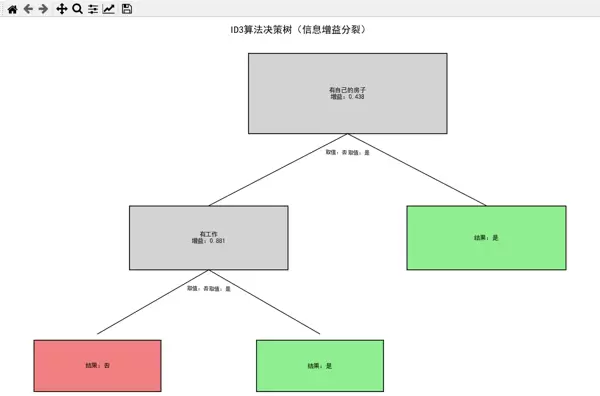
ID3 决策树可视化结果:ID3 决策树的可视化结果中,灰色节点表示分裂特征及信息增益,绿色叶子表示 "批准贷款",红色叶子表示 "拒绝贷款",分支标注了特征的具体取值。
三、CART 决策树:基于基尼系数的二分分裂
CART(分类回归树)是另一种常用的决策树算法,与 ID3 的核心区别在于: 采用基尼系数(而非信息熵)衡量节点纯度 始终进行二分分裂(即使多分类特征也拆分为 "是 / 否" 两组)
1. CART 算法实现(基于 scikit-learn)
借助 scikit-learn 的工具,指定参数来实现 CART:
DecisionTreeClassifiercriterion='gini'def build_cart_tree(X, y, max_depth=3):
# 特征编码(CART需要数值输入)
label_encoders = {}
for col in X.columns:
le = LabelEncoder()
X[col] = le.fit_transform(X[col])
label_encoders[col] = le
# 标签编码
y_le = LabelEncoder()
y_encoded = y_le.fit_transform(y)
# 构建CART树
cart_model = DecisionTreeClassifier(criterion='gini', max_depth=3, random_state=42)
cart_model.fit(X, y_encoded)
return cart_model, label_encoders, y_le2. CART 决策树的可视化
使用 scikit-learn 内置的函数进行可视化:
plot_treeplt.figure(figsize=(12, 8))
plot_tree(
cart_model,
filled=True,
rounded=True,
feature_names=X.columns,
class_names=y_le.classes_,
fontsize=10
)
plt.title("CART算法决策树(基尼系数分裂)", fontsize=14)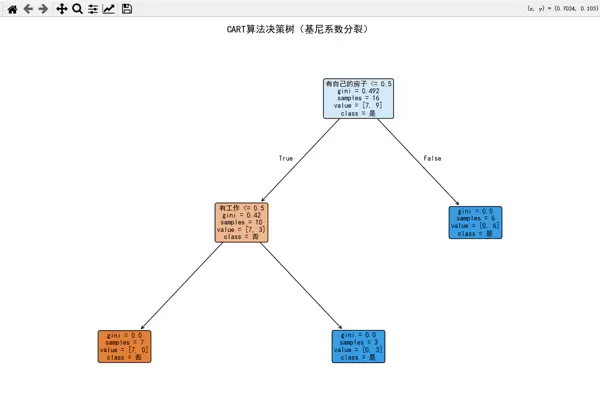
CART 决策树可视化结果:CART 决策树的可视化结果显示了分裂特征、阈值、基尼系数及样本分布,颜色越深表示节点纯度越高(基尼系数越小)。
四、两种算法的性能对比
我们通过同一测试样本(青年、有工作、无房、信贷好)来对比预测结果,并分析分裂逻辑差异:
# 测试样本
test_sample = {
"年龄段": "青年", "有工作": "是", "有自己的房子": "否", "信贷情况": "好"
}
# ID3预测结果:是
# CART预测结果:是2. 核心差异分析
| 对比维度 | ID3 算法 | CART 算法 |
|---|---|---|
| 分裂依据 | 信息增益(熵) | 基尼系数 |
| 分裂方式 | 多叉分裂(特征有多少值分多少支) | 二分分裂(始终拆分为两组) |
| 特征处理 | 仅支持离散特征 | 支持离散 / 连续特征 |
| 过拟合风险 | 较高(易受噪声影响) | 较低(二分分裂更稳健) |
五、总结与拓展
适用场景:
- ID3 适合特征离散且追求高解释性的场景(如规则推导)
- CART 适合处理混合类型特征或需要剪枝优化的场景(如工业级模型)
优化方向:
- 剪枝处理(降低过拟合风险)
- 特征连续化(CART 可直接处理连续特征)
- 集成学习(如随机森林,基于决策树的强分类器)
通过本文的实战对比,相信你已掌握决策树的核心逻辑与实现方法。完整代码可直接运行,建议替换为自己的数据集进行调试,进一步理解两种算法的特性。




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







