对该指数增长模型的稳健性与不确定性分析技术实现的效果感兴趣的读者,可以访问以下链接进行观察与体验:
技术实践观察地址:
FIRE之旅 财务计算器
摘要:
财务独立(FIRE)的实现依赖于对长期投资不确定性的精准建模。本文将从金融工程的角度,探讨如何超越传统的确定性复利模型,通过引入不确定性分析,特别是**蒙特卡洛模拟(Monte Carlo Simulation)**的思想,来评估财务规划的稳健性。我们将分析如何通过可视化工具,实现对核心变量(如投资回报率、通货膨胀率)波动性的建模与路径规划。
一、确定性模型的局限性:指数增长背后的“灰犀牛”
传统的复利模型(A_{t+1} = A_t \times (1 + r) + S)是一种确定性模型。它假设投资回报率r和通货膨胀率\pi在整个投资周期内是恒定不变的。然而,在真实的金融市场中,r和\pi都是高度**随机(Stochastic)且不确定(Uncertain)**的变量。这种确定性模型的局限性在于:
- 无法反映市场波动:资产的增长并非一条平滑的指数曲线,而是受宏观经济周期影响的随机游走过程。
- 低估了序列风险(Sequence of Returns Risk):退休初期(或FIRE初期)的市场连续下跌,对投资组合的长期生存能力具有灾难性的影响,而确定性模型无法捕捉这种风险。
要构建一个具备**稳健性(Robustness)**的FIRE规划,必须将不确定性集成到模型中。
二、技术深潜:不确定性分析与蒙特卡洛的思想应用
解决金融模型不确定性的最核心技术,是蒙特卡洛模拟(Monte Carlo Simulation)。蒙特卡洛模拟的核心机制:
- 其基本思想是:不为r和\pi设定一个固定的值,而是为它们设定一个概率分布(通常是基于历史数据的正态分布或历史波动率),然后让计算机进行成千上万次模拟。
- 在每一次模拟中,模型会随机抽取一个r和\pi的值,并计算出一条独一无二的资产增长路径。
- 通过运行数万次模拟,可以得到一个概率分布的退休年龄/资产值结果,例如:“有95%的概率在50岁前退休”。
序列风险(SORR)的建模:
- 先进的FIRE模型必须能模拟序列风险。这要求在蒙特卡洛模拟中,不能简单地独立抽取每年的回报率。相反,它应该:基于历史数据进行抽样:从真实的、长期的市场历史数据中抽取连续的时间窗口作为模拟的r值输入,以反映连续牛市或熊市对资产的真实影响。
- 失败率分析:模型通过计算在所有模拟路径中,资产在特定时间点(如退休30年后)耗尽的次数,来评估**“安全提款率(4%)”**的实际失败概率。
- 高级建模的变量集成:除了r和\pi,一个复杂的模型还需要集成更多变量:
税收:考虑不同账户(如退休金账户、普通投资账户)的税务差异,对最终可提现资产进行折算。
支出弹性:引入退休后支出的调整机制,例如允许在熊市时减少支出,增强规划的弹性。
三、技术价值的观察与应用场景
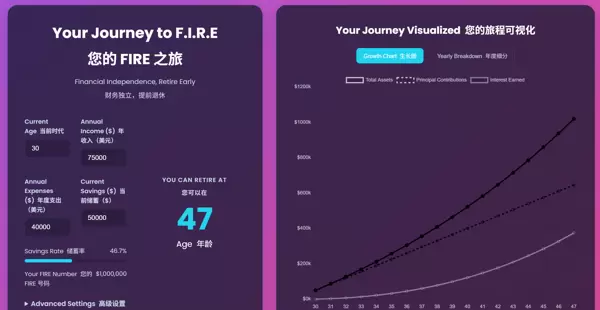
将这种复杂的蒙特卡洛思想和不确定性分析能力封装成用户可交互的Web工具,极大地提高了个人财务规划的科学性和严谨性。一个名为 Your Journey to F.I.R.E. 的Web应用,将核心的指数增长模型与高级设置相结合。虽然界面可能没有直接显示数万次的模拟结果,但其底层计算逻辑和高级设置中对回报率和通胀率的参数化设计,体现了对不确定性建模的思想。
该工具的价值在于:
- 路径的概率化理解:它引导用户从“一定会发生”的确定性思维,转向“在何种概率下能实现”的概率化思维。
- 关键指标的聚焦:通过计算并展示储蓄率,它将复杂的金融问题简化为用户唯一可控的变量,指导用户进行最有效的行为调整。
该工具通过严谨的金融建模思维,提升了个人财务规划的科学性和长期稳健性。
四、总结与展望
对FIRE目标的追求,是对长期不确定性进行精准建模的金融工程实践。通过超越传统的确定性复利模型,引入蒙特卡洛模拟的思想和序列风险分析,我们可以构建一个更具稳健性的财务规划。这类Web工具的出现,使得复杂、科学的金融不确定性分析不再是专业投资机构的专利,而成为个人规划的技术支撑。




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







