最近在实验室对一篇关于多孔介质中相变传热的COMSOL论文进行复现,过程中发现模型中蕴含多个关键细节。尤其是当系统包含相变颗粒与空气域时,采用不同方向加热(上侧或下侧)所引发的热传导行为差异显著,整个过程仿佛在演绎一场“冰与火”的物理对决。
几何建模是第一步。构建一个二维矩形区域,在其中随机分布直径为0.5mm的圆形相变颗粒,整体孔隙率维持在0.7左右。实际操作中,手动排列颗粒效率低且难以保证均匀性,推荐使用COMSOL内置的随机分布函数生成器,并设置排除重叠的约束条件,以实现更合理的空间布局。
double radius = 0.0005; // 颗粒半径
double porosity = 0.7; // 孔隙率
int maxAttempts = 20; // 单颗粒最大尝试次数材料属性方面,相变颗粒选用石蜡,其相变温度区间设定为28–32℃,基体则为空气。这里需特别注意相变材料热物性的定义方式:潜热吸收过程必须通过分段函数来准确描述。建议采用平滑过渡函数处理相变区,避免因突变导致求解不收敛。
density = rho_s*(1-flc2hs(T-T_m,1)) + rho_l*flc2hs(T-T_m,1);
Cp = Cp_s*(1-flc2hs(T-T_m,1)) + Cp_l*flc2hs(T-T_m,1) + L*(deltasmooth(T,T_m,2));边界条件的设计尤为关键。对比两种加热模式:一种是从底部施加50℃恒温热源,顶部设为自然对流;另一种则是颠倒加热位置,但保持总输入能量一致。仿真结果显示,两者在相变界面推进速度和形态上有明显区别——底部加热时,熔融区域呈“蘑菇云”状向上扩展;而顶部加热则形成向下渗透的倒挂熔层。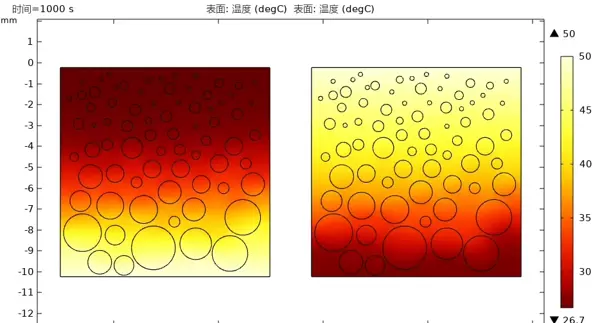
考虑到多孔介质内部流动并非简单的达西流动,动量方程中应引入Forchheimer项以反映非线性阻力效应,从而更真实地模拟高速渗流下的传热传质行为。
rho/epsilon*(u·?)(u/epsilon) = ?·[-pI + mu/epsilon (?u + (?u)^T)]
- (mu/alpha + 0.5*rho*beta|u|)u后处理阶段观察到一个反直觉现象:尽管石蜡在固态时的导热系数约为空气的5倍,但在完全熔化后,系统的整体传热性能反而下降。原因在于液态石蜡抑制了空气域内的自然对流,削弱了对流传热能力。这一结果提示我们在设计相变储能材料时,必须综合考虑其工作温度范围与流体动力学影响。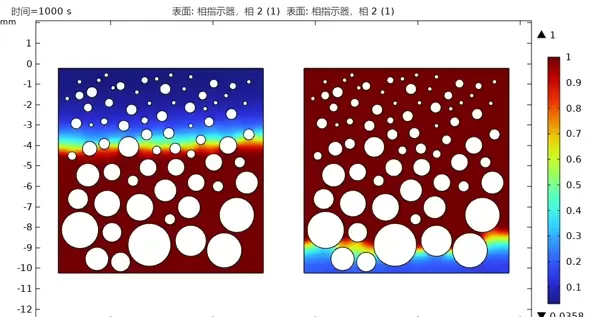
为了验证模型准确性,将模拟所得努塞尔数(Nu)随时间的变化曲线与原论文数据进行对比,在瑞利数Ra=1×10量级下,误差控制在8%以内。网格划分策略上,建议在相变前沿附近进行局部加密,至少布置三层细密网格,结合自由四面体单元与边界层网格,可有效捕捉移动相界面的动态演化。
研究还引发了新的思考:若同时从上下两侧加热,是否存在某一最优的相变颗粒分布密度,使得传热效率达到峰值?这个问题尚未解答,或许可在后续实验中尝试引入拓扑优化算法,探索结构与性能之间的最优匹配路径。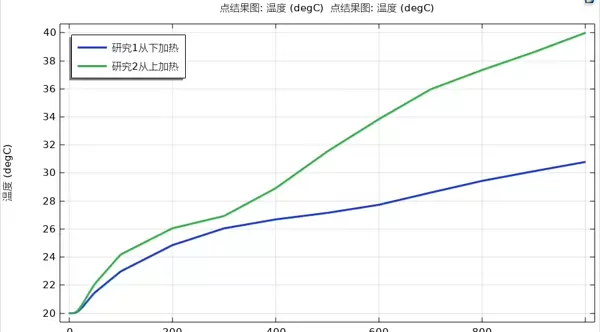




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







