在多元线性回归分析中,解释变量之间若存在较强的相关性,则可能引发多重共线性问题。本文系统梳理了多重共线性的定义与识别方法,并介绍了常见的处理策略,结合实际案例展示其应用过程。
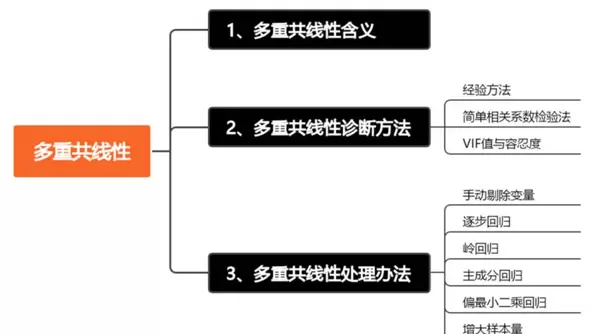
一、多重共线性的基本概念
经典线性回归模型的一个关键假设是自变量之间相互独立。然而在现实建模过程中,多个解释变量之间往往存在不同程度的相关关系,这种现象被称为多重共线性。该问题仅出现在多元回归情境下,弱相关通常对参数估计影响较小,但当变量间存在强线性关联时,会导致回归系数的方差增大,降低估计的精确度和稳定性,使得t检验难以显著,进而无法准确解释各变量对因变量的独立影响。
从数学角度描述,对于如下多元线性回归模型:
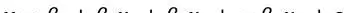
若自变量X之间满足以下条件:存在一组不全为零的常数C,使得

成立,则称这些自变量之间存在多重共线性。
二、多重共线性的诊断方式
判断模型是否出现多重共线性,常用的方法主要包括以下几种:
- 观察回归结果中R较高、F检验显著,但多数变量的t检验不显著;
- 计算自变量之间的Pearson相关系数;
- 使用方差膨胀因子(VIF)或容忍度进行量化评估。
下面以知网发布的一篇研究为例进行说明:
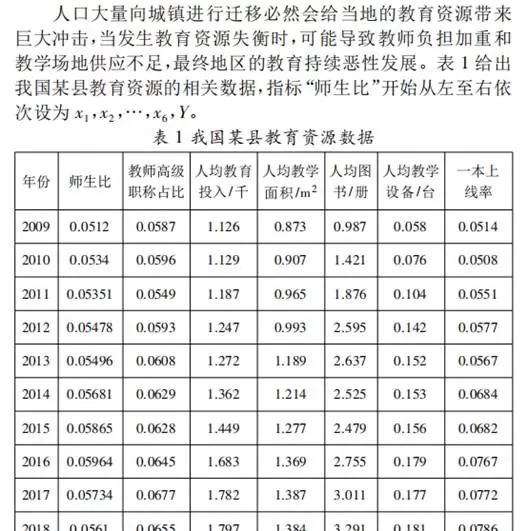
范圣岗、奚书静在《多元线性回归模型中处理多重共线性方法对比——以人口迁移冲击教育资源模型为例》一文中,利用整理后的数据上传至SPSSAU平台,开展共线性诊断及后续建模分析。
1. 经验判断法
当回归模型的拟合优度R很高,整体F检验通过,但多个自变量的t检验未通过,或者回归系数符号不符合经济逻辑时,可初步怀疑存在多重共线性。
如以下回归分析结果所示:
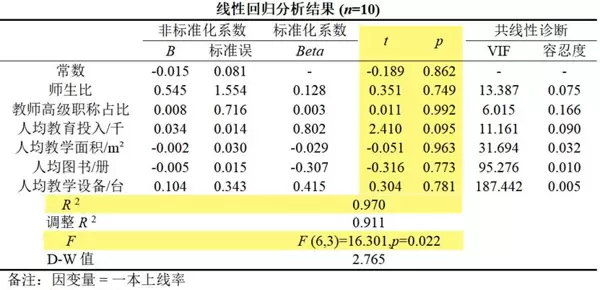
根据经验法则,该模型R=0.970,表明拟合效果良好且F检验显著,但部分变量t检验不显著,提示可能存在多重共线性。此外,SPSSAU输出结果中的VIF值与容忍度也同步提示了共线性问题的存在。
2. 相关系数检验法
若两个或多个自变量之间的Pearson相关系数接近1,说明它们高度相关,可能存在多重共线性。此方法适用于初步筛查。
在SPSSAU【进阶方法】模块中,可通过【共线性分析】功能执行此项检验,用户可设定判断标准,默认阈值为0.6,操作界面如下:
分析结果将输出各变量间的Pearson相关系数、VIF值以及容忍度:
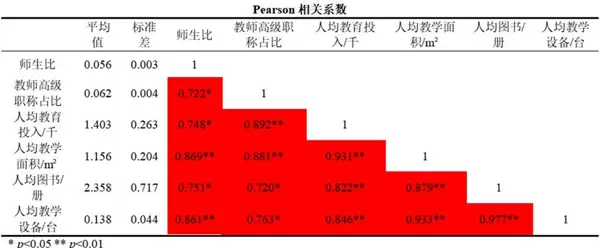
结果显示,所有自变量之间的相关系数均超过0.7且统计显著,表明变量间具有较强的线性关系,初步判定存在多重共线性。
3. VIF值与容忍度分析
方差膨胀因子(VIF)是衡量共线性严重程度的重要指标。一般认为,若VIF>10,即存在较严重的多重共线性问题(严格标准为大于5)。
第i个变量的VIF计算公式如下:
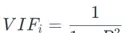
其中Ri表示将第i个自变量作为因变量,对其余自变量做回归所得的决定系数。VIF越大,说明该变量与其他自变量的相关性越强。
另有文献采用“容忍度”作为判断依据,其定义为VIF的倒数。通常认为容忍度小于0.1即存在共线性(更严格标准为小于0.2)。实践中二者任选其一即可,普遍使用VIF进行报告。
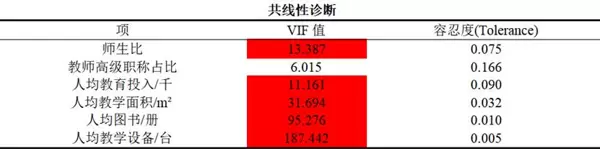
从当前分析结果来看,除“教师高级职称占比”外,其余变量的VIF均高于10,说明模型中存在明显的多重共线性问题。
三、多重共线性的应对策略
面对多重共线性,常用的解决方法包括以下六类:
- 手动剔除高VIF变量
- 逐步回归法
- 岭回归(Ridge Regression)
- 主成分回归(PCR)
- 偏最小二乘回归(PLS)
- 增加样本量
接下来结合本案例逐一演示具体操作。
1. 手动剔除变量法
识别并移除导致共线性的关键变量,是最直接有效的处理方式。操作步骤如下:
- 第一步:删除当前VIF值最高的变量;
- 第二步:重新计算剩余变量的VIF;
- 循环执行:重复上述过程,直到所有变量的VIF≤10(或更严格的5)为止。
在本例中,首先剔除VIF最大的变量“人均数学设备/台”,重新分析后结果如下:
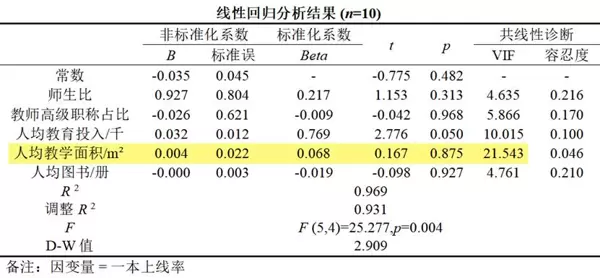
可见其余五个变量的VIF值均有下降趋势。接着继续剔除当前VIF最高的变量“人均教学面积/m”,得到新结果:
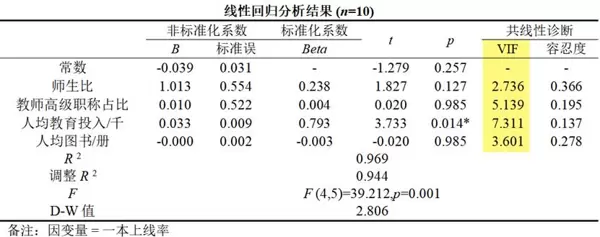
此时剩余四个变量的VIF均低于10,满足要求。最终回归模型表达式为:
一本上线率 = -0.039 + 1.013×师生比 + 0.010×教师高级职称占比 + 0.033×人均教育投入/千 - 0.000×人均图书/册
各系数方向符合预期逻辑,且模型R为0.969,显示良好的解释力与统计显著性。
2. 逐步回归法
在构建回归模型时,逐步回归法是一种常用的变量筛选方法。该方法通过逐个引入解释变量,并结合经济意义检验、统计显著性检验以及R的变化情况,判断是否应保留新加入的变量。若新增变量能通过经济逻辑与统计检验,同时提升模型拟合优度(R方),则予以保留;反之,若R未明显改善,或导致模型解释不合理、变量不显著,则不应引入。
SPSSAU平台提供了三种实现逐步回归的方式:逐步法、向前法和向后法,具体操作界面如下所示:
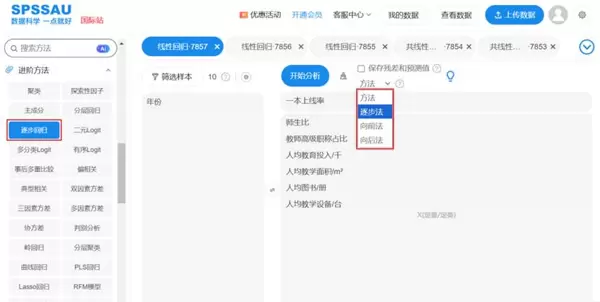
(1)逐步法
该方法融合了“向前选择”与“向后剔除”的机制,属于动态筛选过程。每次有新变量进入模型后,系统会重新评估已入选变量的显著性,若发现某些变量不再具有统计意义,则将其剔除。这一“进—出”循环持续迭代,直至获得一个相对最优的变量组合。
(2)向前法
从空模型出发,依次考察所有候选变量,每次挑选对模型贡献最大且具备统计显著性的变量纳入模型,直到没有符合进入标准的变量为止。这种方法结构简单,倾向保守,在变量选择中较为谨慎。
(3)向后法
起始模型包含全部自变量,随后逐步移除最不显著或影响最小的变量,每步仅删除一个,直到剩余变量均满足保留条件。此方法适用于初始变量较多、样本量充足的情形。
使用SPSSAU的逐步法进行建模分析,最终结果如下:
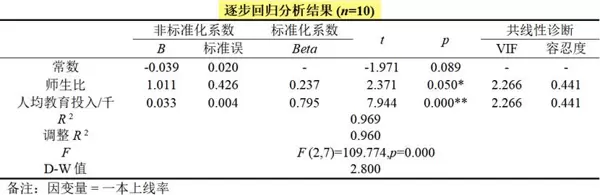
结果显示,仅有“师生比”和“人均教育投入/千”两个变量被保留在最终模型中,且各自方差膨胀因子(VIF)均低于5,表明多重共线性问题得到有效控制。
注意:无论采用手动剔除还是自动逐步回归策略,虽然可在一定程度上缓解共线性,但也可能误删具有理论价值的重要变量,从而偏离研究初衷,需谨慎对待。
3、岭回归
岭回归通过在最小二乘估计中引入L2正则化项(即惩罚项),以适度牺牲无偏性为代价,换取参数估计稳定性的提升,避免回归系数过度放大,进而降低模型方差,提高预测精度。
其分析流程主要包括两个步骤:
- 结合岭迹图确定最优K值
- 输入选定的K值执行回归建模
SPSSAU操作示意如下:
(1)依据岭迹图选取最佳K值
SPSSAU输出的岭迹图如下:
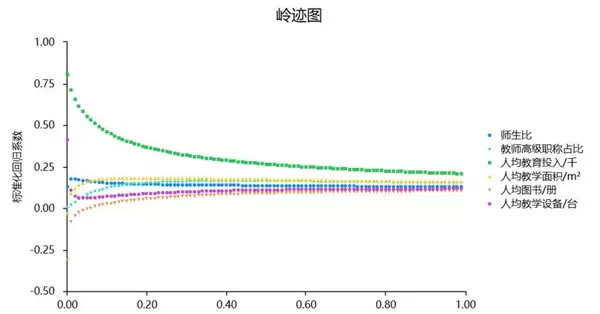
K值的选择至关重要,通常依赖于岭迹图走势与VIF指标综合判断。当各回归系数趋于平稳时对应的最小K值被视为理想选择。尽管该过程具有一定主观性,但可通过辅助信息增强判断准确性。
此外,SPSSAU还提供标准化回归系数随K变化的过程数据及对应VIF值,部分中间结果展示如下:
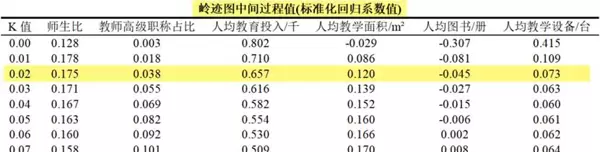
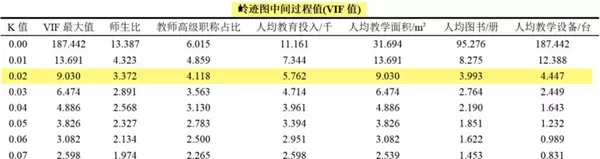
系统基于“VIF ≤ 10”和“K值尽可能小”两项准则,智能推荐K = 0.02作为合适取值。
(2)设定K = 0.02,重新运行岭回归
再次分析后,SPSSAU输出结果如下:
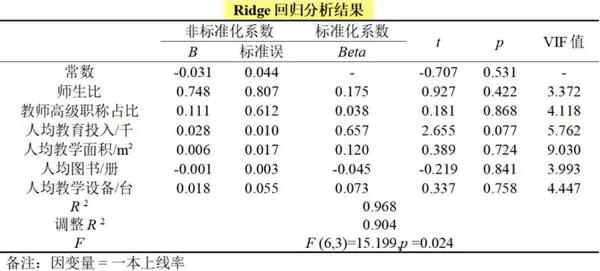
分析可见,所有变量的VIF值均小于10,说明多重共线性问题已基本解决。
提示:尽管岭回归有助于减小估计方差并改善数值稳定性,但如果原始模型本身存在结构性或理论层面的问题(如经济含义不合理),即使应用岭回归也无法保证修正后的模型具备合理的解释力。因此,该方法并非适用于所有类型的共线性问题。
4、主成分回归
主成分回归基于降维思想,在尽可能保留原始信息的前提下,将多个相关性强的指标经正交变换转化为少数几个互不相关的综合变量(主成分),再利用这些主成分建立回归模型。
其核心思路是:先通过主成分分析提取主要信息成分,然后以主成分为自变量对因变量做回归,最后根据主成分与原变量的关系,反推出原始变量的回归方程。
(1)计算主成分得分
在SPSSAU中执行主成分分析,并勾选【成分得分】选项,操作如下图所示:
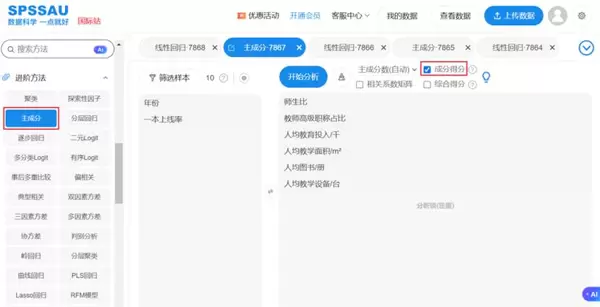
本案例中各指标高度相关,故仅提取一个主成分,累计方差解释率达86.76%。下表为各原始变量在该主成分上的载荷系数:
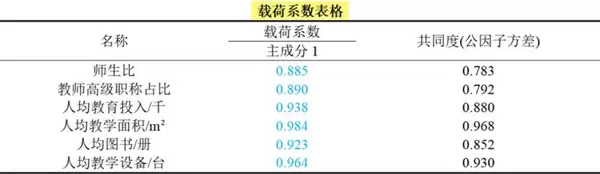
主成分得分表达式为:
PC1 = 0.885×Z1 + 0.890×Z2 + 0.938×Z3 + 0.984×Z4 + 0.923×Z5 + 0.964×Z6
其中Z1至Z6为原始变量的标准形式,SPSSAU将自动保存PC1得分,无需手动计算。
(2)用主成分得分对因变量进行线性回归
回归模型如下:
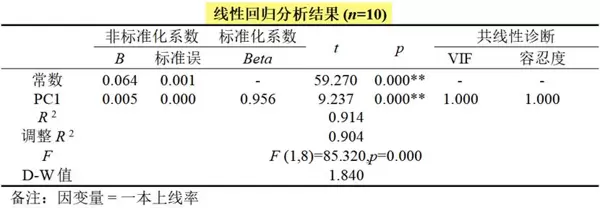
模型公式为:Y = 0.064 + 0.005×PC1
(3)将主成分回归系数还原至原始变量尺度
将PC1代入上述模型可得:
Y = 0.064 + 0.004425×Z1 + 0.00445×Z2 + 0.00469×Z3 + 0.00492×Z4 + 0.004615×Z5 + 0.00482×Z6
若需得到关于原始非标准化变量的回归方程,可利用标准化公式 Z = (X - μ)/σ 进行逆变换,将Z还原为X,进而获得原始尺度下的回归表达式。具体转换过程略去。
5、偏最小二乘回归
偏最小二乘回归(PLS回归)是一种多元统计分析方法,能够有效应对共线性问题、支持多个因变量Y的同时建模,并适用于小样本条件下的影响关系探究。
从方法论角度看,PLS回归融合了三种经典统计技术:主成分分析、典型相关分析以及多元线性回归。其中,主成分分析用于对多个自变量X或多个因变量Y的信息进行降维与浓缩;典型相关分析则侧重于揭示多维X与多维Y之间的整体关联结构;而多元线性回归主要用于探讨变量间的具体影响路径和方向。PLS回归正是将这三者有机结合,从而在复杂数据情境下实现稳健建模。
以下为使用SPSSAU软件进行PLS回归的操作示例:
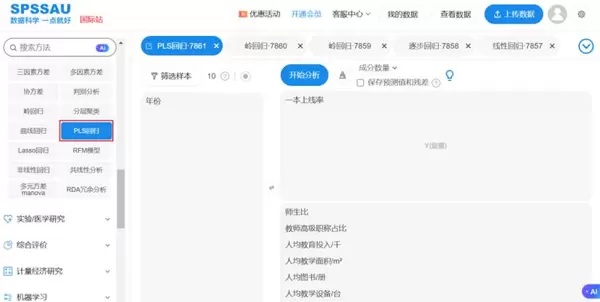
关于多重共线性的处理,增加样本量也是一种常见思路。理论上,当变量的观测值较少时,模型更容易出现共线性现象。因此,扩大样本规模可能有助于缓解这一问题。然而,在实际应用中该方法存在局限性:一方面难以预判所需的具体样本增量,另一方面新增数据可能引入新的干扰因素,反而降低模型拟合效果,无法达到预期目标。




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







