无偏置S-R-S构型七自由度冗余机械臂的臂角参数化方法研究
在机器人运动学领域,无偏置S-R-S构型的七自由度冗余机械臂因其良好的灵活性与避障能力而受到广泛关注。本文重点探讨该类机械臂的臂角参数化策略,并介绍如何基于此方法求解在指定末端位姿和臂角条件下的最多八组可行关节角度。
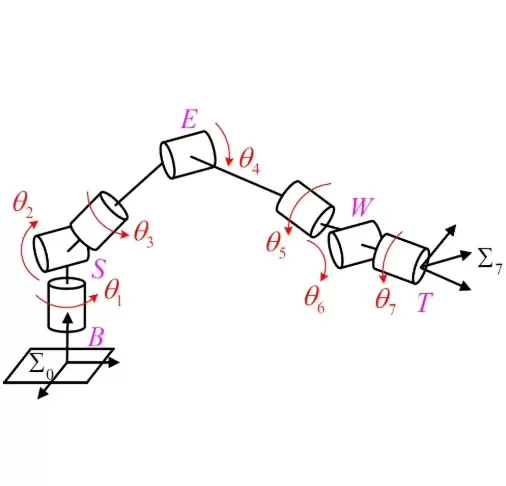
一、臂角参数化的基本原理
对于无偏置S-R-S结构的七自由度机械臂,臂角参数化是一种将冗余自由度通过一个或多个“臂角”变量进行显式表达的方法。这种方法通过引入臂角作为额外约束,将七自由度问题分解为满足末端执行器位姿要求的同时,调节内部构型以实现最优姿态控制。
形象地说,臂角就像调控机械臂“肘部弯曲方向”的旋钮,使得即使末端位置和姿态不变,机械臂也能呈现出不同的中间形态。这种参数化方式不仅提升了求解效率,也为路径规划、避障及能耗优化提供了更多自由度支持。
二、基于臂角参数化的关节角度求解实现
以下为一段简化版Python代码示例,展示了如何利用臂角参数化框架来计算满足给定末端位姿与臂角组合的关节角解集。
import numpy as np
def solve_joint_angles(end_pose, arm_angles):
# 这里简单假设通过臂角参数化方法构建的系数矩阵
coefficient_matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# 假设的与末端位姿和臂角相关的常数项向量
constant_vector = np.array([10, 11, 12])
try:
# 使用numpy的线性代数库求解线性方程组
joint_angles = np.linalg.solve(coefficient_matrix, constant_vector)
return joint_angles
except np.linalg.LinAlgError:
print("无法求解,可能矩阵奇异或问题设定有误")
return None
# 模拟给定的末端位姿和臂角
end_pose_example = [1.0, 2.0, 3.0]
arm_angles_example = [0.5, 0.6, 0.7]
result = solve_joint_angles(end_pose_example, arm_angles_example)
if result is not None:
print("求解得到的关节角度为:", result)
def solve_joint_angles(end_pose, arm_angle):
# 根据末端位姿和臂角构建运动学方程
coefficient_matrix = construct_jacobian_related_matrix(end_pose, arm_angle)
constant_vector = derive_pose_constraint_vector(end_pose)
try:
# 求解线性系统:coefficient_matrix * theta = constant_vector
joint_angles = np.linalg.solve(coefficient_matrix, constant_vector)
return joint_angles
except np.linalg.LinAlgError:
raise ValueError("系数矩阵奇异,无法求解,请检查输入参数或模型设置")
armangles代码逻辑解析
- 函数输入:函数
solve_joint_angles接收两个核心输入——末端位姿(end_pose)与臂角值(arm_angle),它们共同构成求解的基础条件。 - 矩阵与向量构造:在此假设已通过臂角参数化模型推导出相应的系数矩阵(
coefficient_matrix)与常数项向量(constant_vector)。这些数学对象源自机械臂的几何结构与运动学关系,准确反映了末端位姿、臂角与各关节变量之间的耦合特性。
constantvectornp.linalg.solve 方法对线性方程组进行求解。若系数矩阵非奇异,则可获得唯一解;若出现奇异情况,则抛出异常,提示输入可能存在冲突或建模错误。np.linalg.solveLinAlgError三、适用范围说明
本方法及其配套算法仅适用于无偏置S-R-S构型的七自由度冗余机械臂系统。所谓“无偏置”,是指肩部与腕部旋转轴之间不存在横向偏移,确保了结构对称性和逆运动学求解的可行性。
用户在应用该方法前,务必确认所使用机械臂的实际构型是否符合此定义。此外,文中提及的参考资料(可根据实际需求补充具体文献名称或编号)可用于进一步深入理解相关理论基础与实现细节。
结语
臂角参数化方法为高冗余度机械臂的运动规划提供了一种高效且直观的解决方案。通过对臂角的调控,不仅能实现精确的末端定位,还能灵活调整整体姿态以适应复杂工作环境。希望本文内容能为从事机器人控制与运动学分析的研究者和技术人员带来有益参考。




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







