离散数学之关系八大特殊元的求解

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

离散数学中偏序关系下的八大特殊元解析

本文为学习过程中的整理笔记，旨在厘清偏序集中常见的八大特殊元素。由于这些概念在实际判断中容易混淆，因此通过哈斯图辅助理解，并结合具体例子进行说明。

需要注意的是，这八大元仅出现在偏序关系中，而偏序集可以通过哈斯图直观表示。以下分析将以一个整除关系的哈斯图为基础展开：

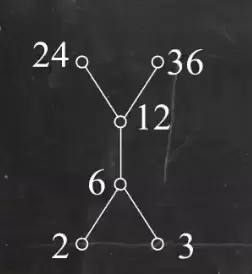
设整个集合为 A，我们从中选取若干子集作为 B 来逐一分析。选取的子集包括：{6,12}、{2,3}、{24,36} 和 {2,3,6,12}。

最大元与最小元

最大元和最小元若存在，则必唯一；但它们也可能不存在。关键点在于：

• 必须从当前子集 B 中寻找，与全集 A 的其他部分无关；
• 所选元素需与其他元素之间存在偏序关系（如“可比”）。

最大元是指在 B 中能够“盖住”所有其他元素的那个元素——即它大于或等于 B 中每一个元素。

• 对于 {6,12}：12 可以整除 6 和自身，故 12 是最大元；
• 对于 {2,3}：两者互不整除，无可比性，因此无最大元；
• 对于 {24,36}：同样无法相互覆盖，没有最大元；
• 对于 {2,3,6,12}：12 能被所有元素整除且能整除自己，是唯一最大元。

最小元则是指在 B 中能被所有其他元素“盖住”的那个元素——即它小于或等于 B 中每一个元素。

• 对于 {6,12}：6 被 12 整除，且不能被 B 中更小者覆盖，因此是最小元；
• 对于 {2,3}：彼此不可比，无最小元；
• 对于 {24,36}：同理，无最小元；
• 对于 {2,3,6,12}：虽然 2 和 3 都是底层元素，但他们之间不可比，无法选出唯一的最小元，因此最小元不存在。

极大元与极小元

为了便于对照观察，再次展示原图：

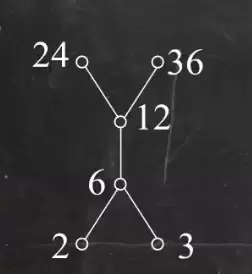
与最大/最小元不同，极大元和极小元不要求元素间有直接关系，也不一定唯一。只要在当前集合 B 中没有更大的（或更小的）元素即可。

极大元：B 中不存在比它更大的元素。

• {6,12}：12 没有后继，是极大元；
• {2,3}：二者均无更大者，所以都是极大元；
• {24,36}：同理，24 和 36 均为极大元；
• {2,3,6,12}：12 是最高可达节点，是唯一的极大元。

极小元：B 中不存在比它更小的元素。

• {6,12}：6 是最小层级，是极小元；
• {2,3}：两者均为底层，不可比较，均为极小元；
• {24,36}：24 和 36 都是叶节点，都是极小元；
• {2,3,6,12}：2 和 3 处于最底层，无法再向下延伸，因此都是极小元。

区别说明：最小元要求与集合中所有元素可比，并且是最小的那个；而极小元只需没有更小者即可，允许存在多个且彼此不可比。最大元与极大元的关系亦然。

特别地，在哈斯图中若某点为孤立点，则它既是极大元也是极小元。

上界与上确界

上界不是从子集 B 内部找，而是考察全集 A 中哪些元素可以同时“盖住”B 中的所有元素。注意：“盖住”意味着必须存在偏序关系。

所有这样的元素构成上界集合，其中的最小元即为上确界（即最小的上界）。

• {6,12}：A 中能整除 6 和 12 的有 12、24、36 → 上界为 {12,24,36}，最小的是 12 → 上确界为 12；
• {2,3}：能同时整除 2 和 3 的是 6、12、24、36 → 上界为 {6,12,24,36}，最小的是 6 → 上确界为 6；
• {24,36}：A 中没有任何元素能同时整除这两个数 → 无上界，也无上确界；
• {2,3,6,12}：能整除该集合所有元素的是 12、24、36 → 上界为 {12,24,36}，最小的是 12 → 上确界为 12。

下界与下确界

下界是从全集 A 中找出所有能被 B 中每个元素“盖住”的元素——即这些元素能整除 B 中的每一个成员。

所有的下界组成一个集合，其中的最大元称为下确界（即最大的下界）。

• {6,12}：能被 6 和 12 同时整除的有 6、3、2 → 下界为 {2,3,6}，最大的是 6 → 下确界为 6；
• {2,3}：没有比它们更小的公共因数（除了1未列出），已处于最底层 → 无下界，无下确界；
• {24,36}：能整除它们的有 12、6、3、2 → 下界为 {2,3,6,12}，最大的是 12 → 下确界为 12；
• {2,3,6,12}：不存在能被其所有元素整除的更小元素 → 无下界，无下确界。

综上所述，以上八种特殊元素构成了偏序集中重要的结构性概念，统称为“八大元”。

练习一

题目如下：

注：题中“特殊元素”即指前述八大元。

解答：首先构造对应的哈斯图：

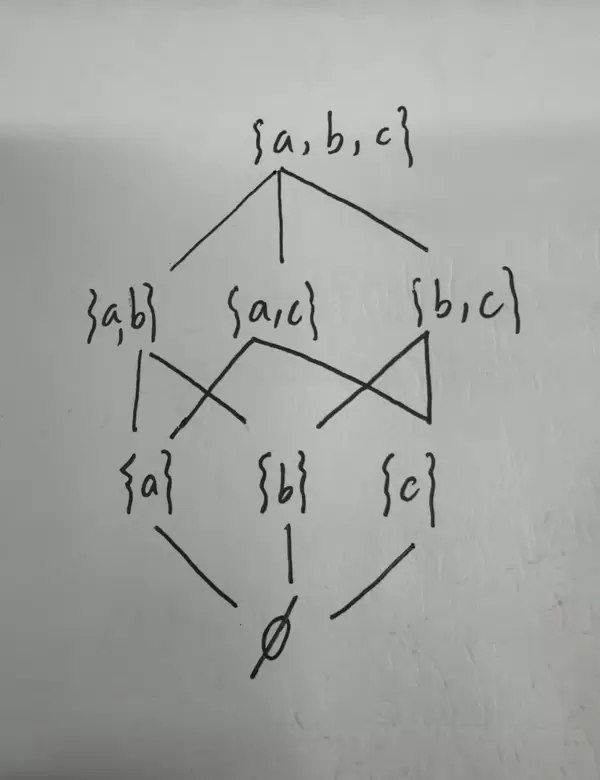
考虑子集 B = {{a}, {c}}，为方便叙述省略括号写作 a, c。

• 最大元：a 与 c 无上下关系，无法互相覆盖 → 不存在；
• 最小元：同理，二者平级 → 不存在；
• 极大元：B 中没有比 a 或 c 更大的元素 → 极大元为 a 和 c；
• 极小元：同理，二者均为极小元；
• 上界：全集 A 中能覆盖 a 和 c 的有 {a,c} 和 {a,b,c} → 上界为这两个集合；
• 上确界：上界中最小的是 {a,c} → 即为上确界；
• 下界：能被 a 和 c 同时覆盖的只有空集 ；
• 下确界：下界仅含 ，因此下确界也为 。

练习二

注：本题中的“特殊元素”仍指八大元。

解答：绘制对应的哈斯图如下：

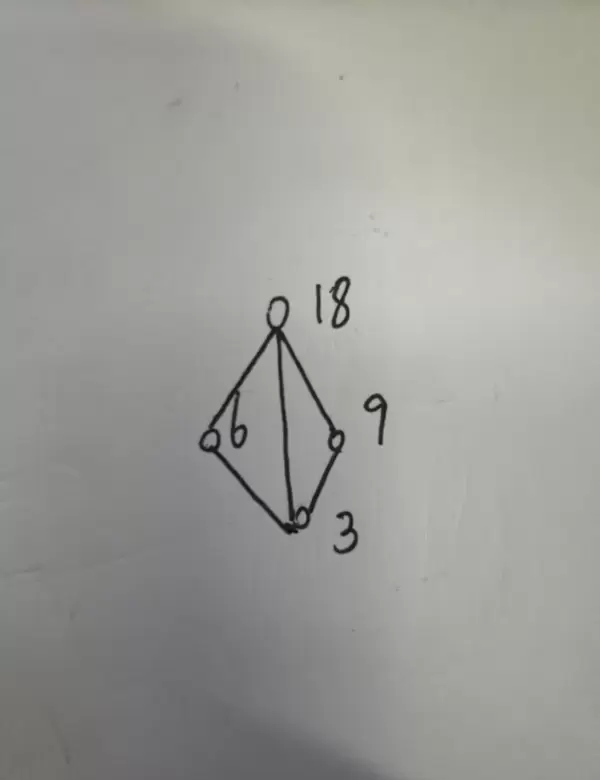
在集合A2中包含元素3、6、9。

关于最大元的判断：由于6和9都能够“覆盖”3，因此最大元只能从6和9中产生。然而，6与9之间不存在可比关系，彼此不构成覆盖关系，故该集合中不存在最大元。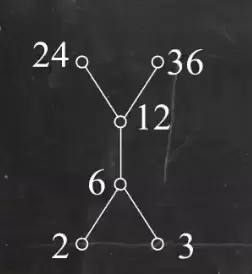

对于最小元的分析：元素3可以被6和9所覆盖，且没有其他更小的元素存在，因此3是该集合中的最小元。

极大元的情况：6和9处于同一层级，互不可比，但都能覆盖3，因此6和9均为极大元。

极小元显然为3，因为没有任何元素比它更“小”或能被它覆盖。

上界与上确界的确定：在整个A集合范围内，唯一能够同时覆盖3、6、9的元素是18，因此18既是上界，也是最小上界，即上确界。

下界与下确界的判断：在所有元素中，3能被其余每个元素覆盖，因此3作为最大的下界，既是下界，也是下确界。

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：离散数学 题目如下 不存在 最大的 最底层