发帖
雷达卡
本章节的内容相较于前几章有明显不同，不再聚焦于随机过程的广泛研究，而是转向一种特定类型的数学模型——用于描述状态随时间演化的系统。这部分内容属于入门级别，理解起来相对容易。
需要注意的是，本章会大量涉及矩阵运算的相关知识，建议提前回顾线性代数中的相关内容，特别是以下两个方面：
- 逆矩阵的求解方法
- 矩阵的基本运算，如矩阵的幂运算
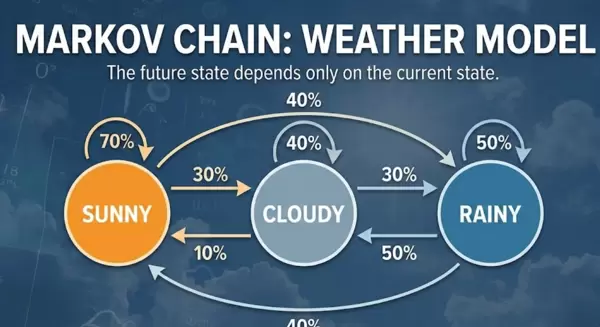
一、整体知识框架
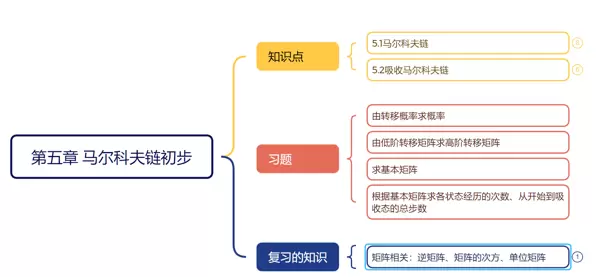
二、具体知识点
1、马尔科夫链简介
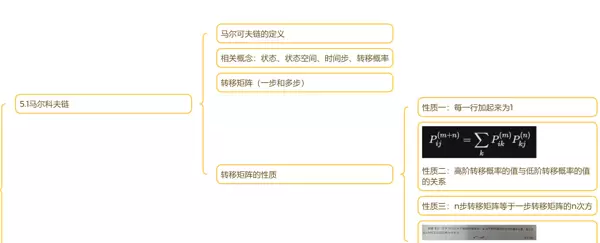
可以用一句话精准概括其核心思想：
“未来仅依赖于当前状态，与过去的历史无关。”
这一特性也被称为：
- 无记忆性（Memorylessness）
- 马尔科夫性质（Markov Property）
要完整定义一个马尔科夫链，通常需要明确三个基本要素：
状态空间（State Space, S）：
表示系统所有可能所处的状态的集合。例如：天气系统的状态可以是{晴, 雨}；股票市场的状态可设为{涨, 跌, 平}。
转移概率（Transition Probability）：
指从状态 i 转移到状态 j 的概率，记作 $P_{ij}$。
转移矩阵（Transition Matrix, P）：
是一个包含所有转移概率的方阵。其中每一行代表从某一状态出发的所有可能转移，因此每行元素之和必须等于 1。
下面是一个直观的例子：
2、吸收马尔科夫链
2.1 简介
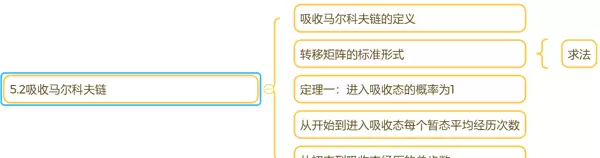
如果说普通的马尔科夫链像是一场没有终点的循环旅程，那么吸收马尔科夫链则更像是一场“有结局”的过程。一旦系统进入某个特殊的终止状态，整个过程就会停止，并且无法再离开该状态。
一个马尔科夫链被称为“吸收马尔科夫链”，必须同时满足以下两个条件：
- 至少存在一个吸收态（Absorbing State）：
即一旦系统进入该状态，则永远停留在此状态，对应的自转移概率为 1（即 $P_{ii} = 1$）。这类似于游戏中的“通关”或“结束”状态。 - 从任意非吸收态出发，最终都有可能到达某个吸收态：
无论经过多少步转移，系统不会永久停留在非吸收态之间循环，而总有机会进入吸收态。
2.2 标准形式
吸收马尔科夫链的转移矩阵可以被整理为如下标准结构：
2.3 关心的两个核心问题
京公网安备 11010802022788号
