基于多策略麻雀搜索算法的机器人路径规划研究解析
近期在探索机器人路径规划领域时,注意到一篇具有创新性的学术论文——《基于多策略麻雀搜索算法的机器人路径规划》,由杨红与杨超发表于《沈阳大学学报(自然科学版)》2024年第36卷第2期(页码:141-152)。该文针对传统麻雀搜索算法存在的局限性,提出了一系列改进措施,并将其应用于复杂环境下的机器人路径优化问题中。以下是对文中关键技术点的梳理与解读。
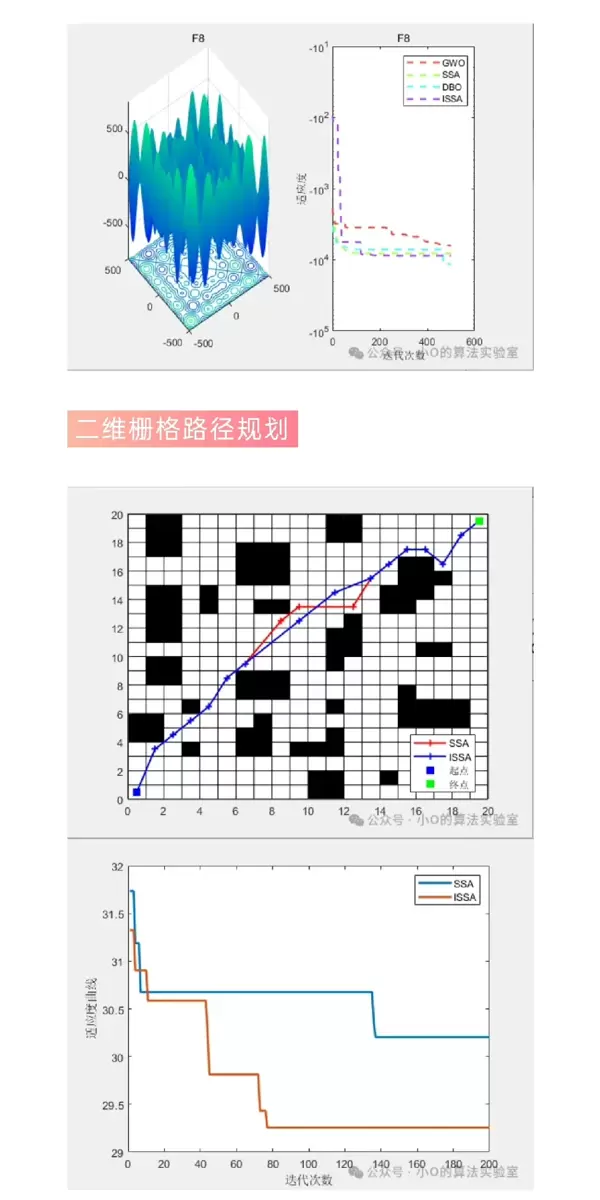
一、核心改进策略分析
1. 引入改进型无限折叠迭代混沌映射
混沌映射因其良好的随机性和遍历特性,常被用于智能优化算法中以增强种群多样性。本文设计了一种新型的“无限折叠迭代混沌映射”,在经典结构基础上进行迭代机制革新,显著提升了序列分布的质量。
例如,传统的Logistic混沌映射表达式为:
$x_{n + 1} = \mu x_n(1 - x_n)$,其中控制参数$\mu$通常取值于$(3.57, 4]$区间内,$x_n$表示第$n$次迭代的结果。
而本文所采用的改进版本则通过条件判断实现分段计算,使生成的混沌序列具备更强的非线性特征和更广的覆盖范围,从而有效提升初始种群的空间分布均匀性,有助于避免早熟收敛。
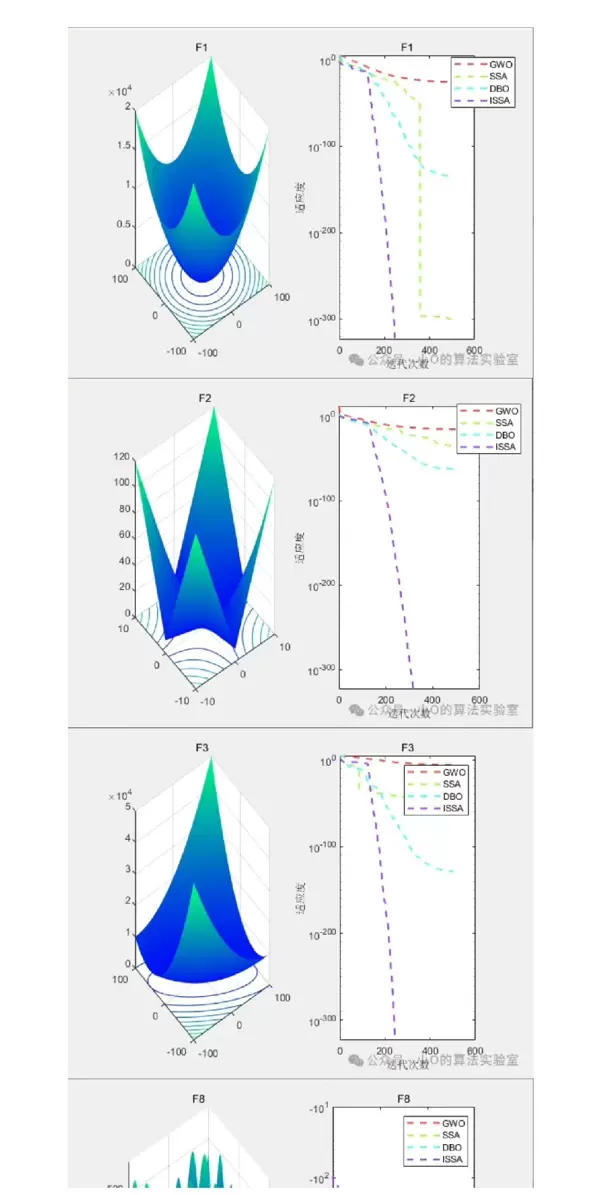
# 假设我们定义一个函数来实现改进的无限折叠迭代混沌映射
def improved_chaotic_map(x0, iter_num):
x = [x0]
for i in range(iter_num):
if x[-1] < 0.5:
x.append(2 * x[-1] * (1 - 2 * x[-1]))
else:
x.append(2 * (1 - x[-1]) * (2 * x[-1] - 1))
return x2. 优化发现者位置更新机制
在麻雀搜索算法中,发现者负责引领全局探索,其更新方式直接影响算法的搜索效率。原公式如:
$X_{i,j}^{t + 1} = X_{i,j}^t(1 + \beta L)$,其中$X_{i,j}^t$代表第$t$代第$i$只麻雀在第$j$维的位置,$\beta$为步长因子,$L$是维度为$1 \times d$的随机向量。
作者在此基础上引入对全局最优解信息的反馈机制,构建了更具导向性的更新逻辑。通过设置概率判断分支,动态调整更新路径,使得发现者在探索过程中既能保持广泛搜索能力,又能快速响应优质区域的引导信号。

import numpy as np
# 假设这里的 pop_size 是种群数量,dim 是维度
def improved_finder_update(X, t, pop_size, dim, best_X):
beta = 0.5
L = np.random.rand(1, dim)
new_X = np.zeros((pop_size, dim))
for i in range(pop_size):
if np.random.rand() < 0.8:
new_X[i, :] = X[i, :] * (1 + beta * L) + np.random.rand() * (best_X - X[i, :])
else:
new_X[i, :] = X[i, :] * (1 + beta * L) - np.random.rand() * (best_X - X[i, :])
return new_Xbest_X3. 动态调节侦察者比例机制
侦察者的作用在于监测潜在风险并协助种群规避局部陷阱。固定比例的设定难以适应不同进化阶段的需求。为此,本文提出一种随迭代进程变化的动态侦察者比例调整策略。
具体而言,在算法初期(前30%迭代次数),由于环境信息匮乏,需加强警戒,将侦察者比例设为0.3;进入中后期后,逐步降低至0.2,以强化局部开发能力。

scout_ratio# 假设 total_pop 是总种群数量
if t < total_iterations * 0.3:
scout_ratio = 0.3
else:
scout_ratio = 0.24. 融合正弦余弦搜索机制
为进一步丰富搜索行为模式,文中还引入正弦余弦算法(SCA)的思想,利用三角函数的周期振荡特性来扰动个体位置,拓展搜索维度。
结合过程可通过如下伪代码形式体现:根据随机变量决定是否启用正弦或余弦项进行位置修正,借助其波动性质帮助算法跳出局部极值区,实现更精细的空间探测。
import math
def sine_cosine_help(X, t, pop_size, dim, best_X):
a = 2
for i in range(pop_size):
for j in range(dim):
r1 = np.random.rand()
r2 = np.random.rand()
if r1 < 0.5:
X[i, j] = X[i, j] + r2 * a * math.sin(r1) * (best_X[j] - X[i, j])
else:
X[i, j] = X[i, j] + r2 * a * math.cos(r1) * (best_X[j] - X[i, j])
return Xr1二、综合评述
本研究围绕麻雀搜索算法展开多项关键性改进,包括混沌初始化机制、发现者更新规则、侦察者比例调控以及外部算法融合等层面,系统性地增强了算法在复杂地形中的路径寻优能力。
通过引入无限折叠混沌映射提升初始多样性,优化发现者公式增强方向感知,动态调整侦察者比例平衡探索与开发,并结合正弦余弦算法增加搜索灵活性,整体框架展现出较强的鲁棒性与实用性。
这些改进为解决高维、多障碍场景下的机器人路径规划提供了新的技术路径,具备较高的复现价值与应用前景。后续可进一步在仿真平台或真实机器人系统中验证其性能表现,推动理论成果向工程实践转化。




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







