一、高维空间的基本认知
在进入主成分分析(PCA)之前,我们首先需要理解高维空间中数据样本的分布特性。
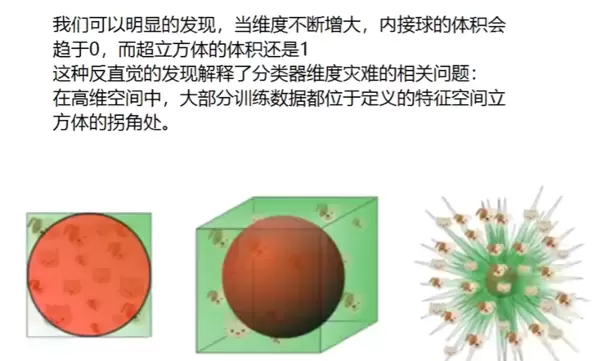
从图中可以看出,当数据集中分布在空间的边缘或拐角区域时,会对后续的数据处理带来较大困难。因此,为了提升模型处理效率与可解释性,通常需要对高维数据进行降维操作。
二、主成分分析(PCA)的应用动机
面对实际数据中特征数量过多的问题,常常会出现“维度灾难”现象——即随着特征维度的增加,数据变得稀疏,计算复杂度急剧上升,同时难以在二维或三维空间中进行有效可视化和分析。此外,过多的冗余特征也可能影响模型性能。
为此,我们引入主成分分析(PCA),其核心目标是通过线性变换将原始高维特征空间投影到一个低维子空间中,在尽可能保留原始信息的前提下减少特征维度。这不仅有助于提升后续分类任务(如拟合线性分类边界)的效果,也极大增强了数据的可视化能力。
三、PCA降维的核心流程
- 给定原始数据矩阵为 m×n 形式(其中 n 表示高维特征数),首先对数据进行去中心化处理,使每个特征的均值为0。
- 基于去中心化后的矩阵,计算其协方差矩阵,用于反映各特征之间的相关性。
- 求解该协方差矩阵的特征值与对应的特征向量。特征值越大,说明对应方向上的数据方差越显著,区分能力越强。
- 将所有特征值按从大到小排序,并选取前 k 个最大特征值所对应的特征向量,构成投影矩阵(维度为 n×k)。
- 最后将去中心化后的原始数据与该投影矩阵相乘,得到降维后的新数据矩阵(m×k),实现由高维向低维的转换。
四、关键概念定义
去中心化:

协方差矩阵的计算公式:
协方差矩阵 = (去中心化矩阵? × 去中心化矩阵) / (m-1)
五、代码实现与解析
我们以经典的鸢尾花数据集为例,展示PCA的实际应用过程。
第一步:导入必要的Python库文件

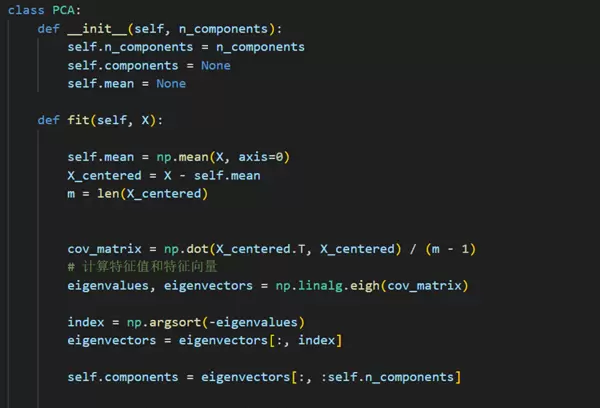
第二步:手动实现PCA算法逻辑。由于本次聚焦原理剖析,故不调用现成库函数,而是自行编码完成整个流程。
具体包括:计算协方差矩阵、提取特征值与特征向量、选择主成分并执行降维操作。
第三步:加载鸢尾花数据集,应用自定义PCA进行降维,并使用KNN分类器训练模型以验证降维后数据的有效性。
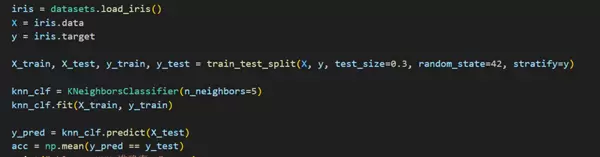
运行结果显示模型具备良好的分类准确率,表明降维过程成功保留了关键判别信息。

接下来,我们将PCA降至2维以便可视化,同时构建KNN分类器进行训练与预测。

最终结果通过图形化方式呈现:
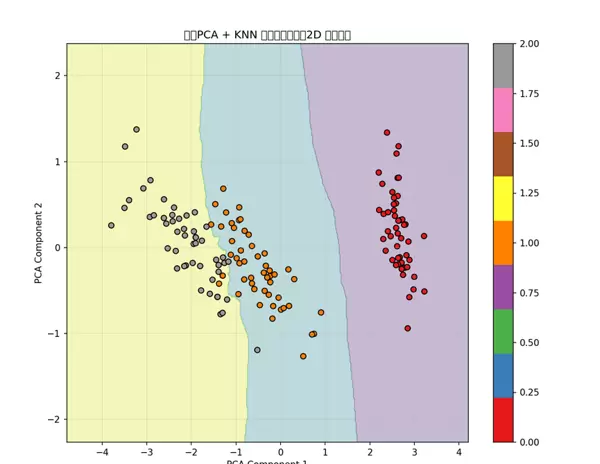
可见,数据成功被压缩至二维空间,且分类边界清晰,模型表现优异,证明PCA在保持结构信息的同时实现了高效降维。
六、完整代码附录
以下为本次实验所使用的全部代码内容:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
class PCA:
def __init__(self, n_components):
self.n_components = n_components
self.components = None
self.mean = None
def fit(self, X):
self.mean = np.mean(X, axis=0)
X_centered = X - self.mean
m = len(X_centered)
cov_matrix = np.dot(X_centered.T, X_centered) / (m - 1)
# 计算特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eigh(cov_matrix)
index = np.argsort(-eigenvalues)
eigenvectors = eigenvectors[:, index]
self.components = eigenvectors[:, :self.n_components]
return np.dot(X_centered, self.components)
iris = datasets.load_iris()
X = iris.data
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, stratify=y)
knn_clf = KNeighborsClassifier(n_neighbors=5)
knn_clf.fit(X_train, y_train)
y_pred = knn_clf.predict(X_test)
acc = np.mean(y_pred == y_test)
print("sklearn KNN 准确率:", acc)
print("\n使用手写PCA进行降维...")
my_pca = PCA(n_components=2)
X_vis = my_pca.fit(X)
print("PCA转换后的数据形状:", X_vis.shape)
print("PCA主成分形状:", my_pca.components.shape)
X_train2, X_test2, y_train2, y_test2 = train_test_split(X_vis, y, test_size=0.3, random_state=42, stratify=y)
knn_vis = KNeighborsClassifier(n_neighbors=5)
knn_vis.fit(X_train2, y_train2)
# 创建网格用于可视化决策边界
h = 0.02
x_min, x_max = X_vis[:, 0].min() - 1, X_vis[:, 0].max() + 1
y_min, y_max = X_vis[:, 1].min() - 1, X_vis[:, 1].max() + 1
xx, yy = np.meshgrid(
np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h)
)
# 预测网格点的类别
Z = knn_vis.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# 可视化结果
plt.figure(figsize=(10, 8))
plt.contourf(xx, yy, Z, alpha=0.3)
scatter = plt.scatter(X_vis[:, 0], X_vis[:, 1], c=y, edgecolor='k', cmap=plt.cm.Set1)
plt.title("手写PCA + KNN 对鸢尾花分类(2D 可视化)")
plt.xlabel("PCA Component 1")
plt.ylabel("PCA Component 2")
plt.colorbar(scatter)
plt.grid(alpha=0.3)
plt.show()



 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







