发帖
雷达卡
在电机控制领域，永磁同步电机（PMSM）由于其高效率、高功率密度等优势被广泛应用于工业与新能源系统中。然而，在实际运行过程中，三相电流或电压的不对称现象时有发生，这种工况会显著影响电机的控制性能和参数估计精度。本文重点探讨在三相不对称条件下对PMSM定子电阻进行参数辨识的方法。
该方程充分考虑了各相间可能存在的参数差异，如每相电阻、电感的不一致性，并将其纳入统一数学框架。这一过程虽涉及较复杂的数学处理，但核心思想清晰：即通过扩展原有模型结构，使其具备描述非对称运行的能力。
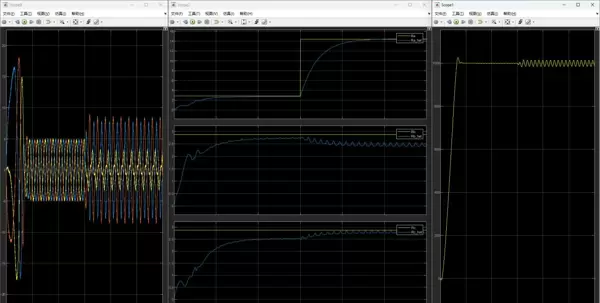
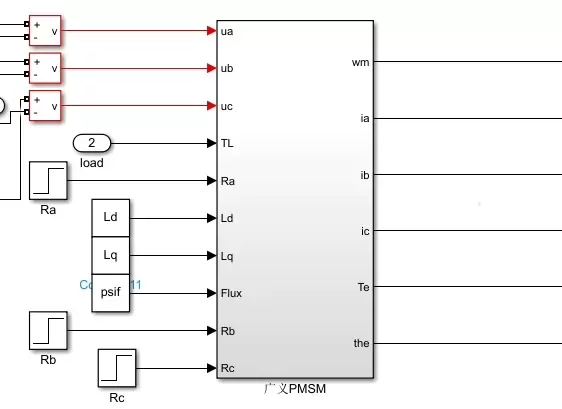
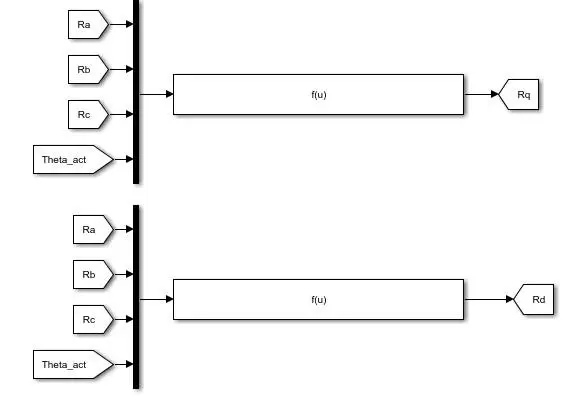
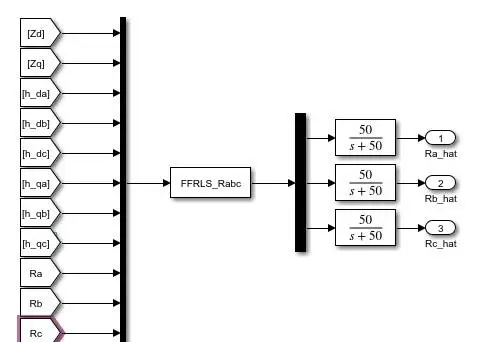为实现仿真验证，需将上述方程转化为可计算的系统模型。建模过程类似于构建一个精确的虚拟电机系统，其中定子电阻、电感、反电动势及外部输入信号均以变量形式嵌入。图一至图三（文中以图片标记示意）展示了关键建模思路与结构参考，包括电机拓扑、磁场分布以及各变量之间的耦合关系，为后续算法设计提供支撑。
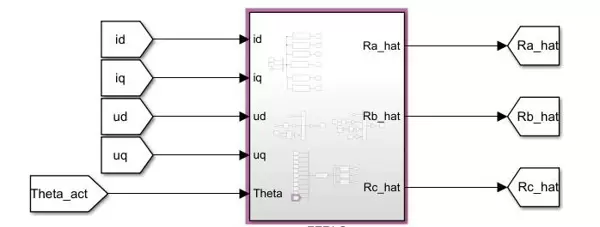
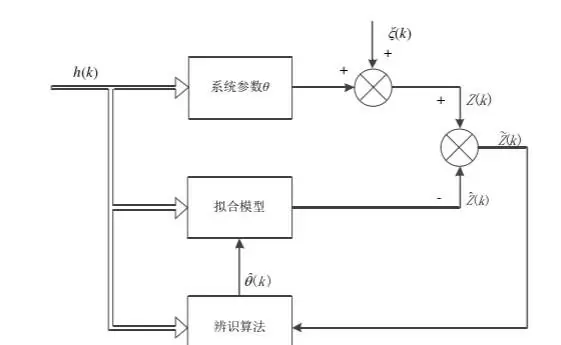FFRLS的核心在于利用实时采集的电压与电流数据，不断更新参数估计值，并通过引入遗忘因子加强对新数据的权重，从而提升动态响应能力。整个算法逻辑通过Simulink中的s-function模块进行封装实现。
s-function相当于一个自定义功能模块，允许用户以C或MATLAB语言编写底层运算逻辑。以下为简化的代码结构示例（仅作示意，非完整实现）：
测试结果表明，即便在系统出现明显不平衡的情况下，基于FFRLS的辨识方法仍能快速且准确地追踪定子电阻的变化趋势，体现出良好的动态性能与稳定性。整个仿真平台完全由手工搭建，涵盖从理论建模到算法编程的全部环节，确保每个细节可控、可解释。
此外，相关研究成果已整理成完整论文，涵盖详细的数学推导、仿真实验设置及对比分析，可供进一步学习与参考。
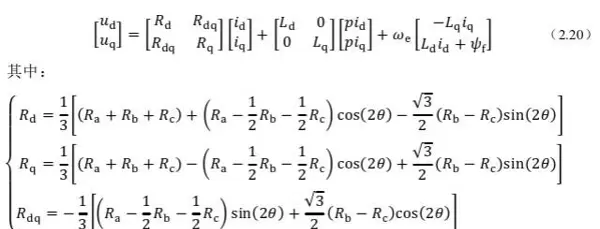通过本研究可见，在三相不对称运行条件下，结合广义电压模型与先进辨识算法，能够有效提升PMSM关键参数的估计精度，为高性能电机控制策略的设计提供了可靠的数据支持。
1. 广义PMSM电压方程的推导与系统建模
面对三相不对称的工作状态，传统对称假设下的电压模型已无法准确描述电机行为，因此需建立适用于该工况的广义电压方程。基于电磁感应定律和电机基本电路关系，从定子绕组的电压-电流-磁链动态特性出发，经过严谨的理论分析，可推导出包含不对称因素的广义PMSM电压表达式。
该方程充分考虑了各相间可能存在的参数差异，如每相电阻、电感的不一致性，并将其纳入统一数学框架。这一过程虽涉及较复杂的数学处理，但核心思想清晰：即通过扩展原有模型结构，使其具备描述非对称运行的能力。
为实现仿真验证，需将上述方程转化为可计算的系统模型。建模过程类似于构建一个精确的虚拟电机系统，其中定子电阻、电感、反电动势及外部输入信号均以变量形式嵌入。图一至图三（文中以图片标记示意）展示了关键建模思路与结构参考，包括电机拓扑、磁场分布以及各变量之间的耦合关系，为后续算法设计提供支撑。
2. 基于FFRLS算法的参数辨识方法与s-function实现
为了在线估计在不对称条件下的定子电阻值，采用递推增广最小二乘法（FFRLS，Forgetting Factor Recursive Least Squares）。该算法具有较强的适应性和收敛性，尤其适合处理存在时变参数与噪声干扰的实际工况。
FFRLS的核心在于利用实时采集的电压与电流数据，不断更新参数估计值，并通过引入遗忘因子加强对新数据的权重，从而提升动态响应能力。整个算法逻辑通过Simulink中的s-function模块进行封装实现。
s-function相当于一个自定义功能模块，允许用户以C或MATLAB语言编写底层运算逻辑。以下为简化的代码结构示例（仅作示意，非完整实现）：
function [sys,x0,str,ts] = s_function(t,x,u,flag)
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes;
case 1,
sys=mdlDerivatives(t,x,u);
case 2,
sys=mdlUpdate(t,x,u);
case 3,
sys=mdlOutputs(t,x,u);
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
case 9,
sys=mdlTerminate(t,x,u);
otherwise
DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
end
function [sys,x0,str,ts]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 1;
sizes.NumInputs = 3;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [];
str = [];
ts = [0 0];
function sys=mdlOutputs(t,x,u)
% u 是输入，这里假设包含了与辨识相关的电流、电压等信号
% 简单示例，实际是实现 FFRLS 算法的核心逻辑
resistance_estimate = some_FFRLS_computation(u);
sys(1) = resistance_estimate;flagmdlInitializeSizesmdlOutputssomeFFRLS_computation(u)3. 故障注入与辨识效果验证
为检验所提方法的有效性，在仿真中设定特定时刻人为引入故障，模拟诸如绕组老化、接触不良等导致的三相不对称情形。这种主动“制造故障”的方式有助于评估算法在异常工况下的鲁棒性与跟踪能力。
测试结果表明，即便在系统出现明显不平衡的情况下，基于FFRLS的辨识方法仍能快速且准确地追踪定子电阻的变化趋势，体现出良好的动态性能与稳定性。整个仿真平台完全由手工搭建，涵盖从理论建模到算法编程的全部环节，确保每个细节可控、可解释。
此外，相关研究成果已整理成完整论文，涵盖详细的数学推导、仿真实验设置及对比分析，可供进一步学习与参考。
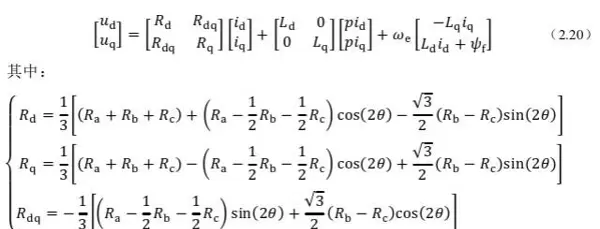通过本研究可见，在三相不对称运行条件下，结合广义电压模型与先进辨识算法，能够有效提升PMSM关键参数的估计精度，为高性能电机控制策略的设计提供了可靠的数据支持。
京公网安备 11010802022788号
