发帖
雷达卡
1. 指数加权平均
在深入学习其他优化算法之前，掌握指数加权平均（Exponentially Weighted Averages）是非常关键的一步。该方法能够有效地对时间序列数据进行平滑处理，帮助我们更好地观察趋势变化。
（1）公式与计算方式
指数加权平均的核心公式如下：
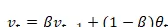
以某年伦敦每日气温为例，原始数据如散点图所示，时间跨度从1月到12月。数据本身较为杂乱，若想提取出整体趋势，可通过局部平均值（即移动平均）来实现。
设定初始值 V = 0，代表第0天的虚拟温度。对于每一天，采用前一天的加权结果乘以系数 β，再加上当天实际温度乘以 (1 - β)。例如，当 β = 0.9 时，相当于用前一日值的90%加上当日温度的10%。
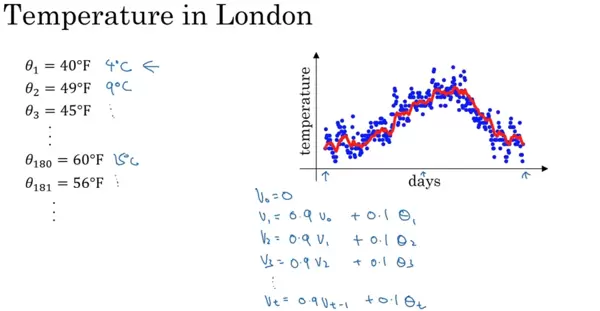
将上述过程用统一符号表示：
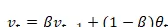
此时，v 可近似看作过去 1/(1β) 天的平均温度。比如：
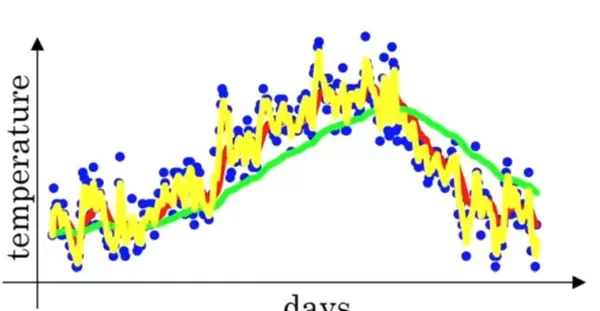
- 当 β = 0.9 时，对应约10天的平均值，反映为图中的红线；
- 当 β = 0.98 时，对应约50天的平均值，表现为绿线，曲线更平稳但滞后更明显；
- 当 β = 0.5 时，仅平均最近两天的数据，得到黄线，波动更大，响应更快。
（2）指数加权平均的理解
继续以上述气温数据为例，假设我们要计算第100天的加权平均温度 v，其表达式为：
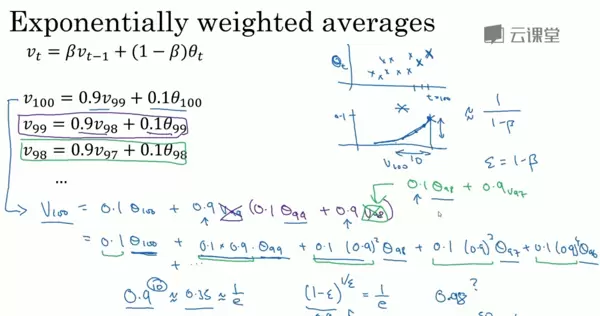
将其展开可得：
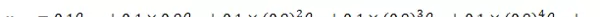
可以看出，权重按照指数形式衰减，因此称为“指数加权平均”。越久远的数据影响越小，呈指数级下降。
这种方法的一大优势在于内存占用极低：只需保存一个当前值，每次接收新数据后更新并覆盖原值即可。整个过程仅需一行代码完成，存储也仅需一个变量空间。虽然它不是最精确的平均方法，但在实时性要求高、资源受限的场景下非常高效。
（3）偏差修正机制
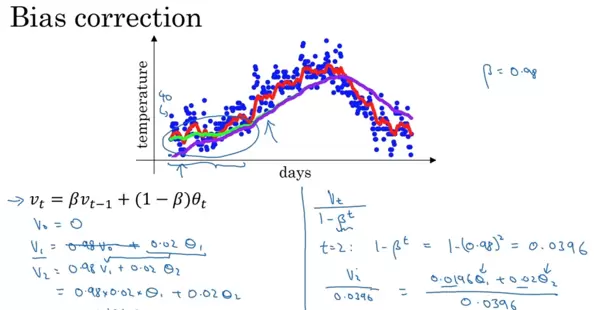
在使用指数加权平均初期，由于起始值设为0，而 β 值较大时（如0.98），初始阶段的平均值会严重偏低，导致估算结果存在明显偏差，缺乏参考意义。
为此引入偏差修正技术，在早期阶段对计算结果进行调整：
v_corrected = v / (1 β)
其中 t 表示当前是第几天。t 越小，修正幅度越大；随着 t 增大，分母趋近于1，修正效果逐渐消失。
例如，在 β = 0.98 的情况下，未修正的曲线为紫色，经过修正后变为绿色，两者随时间推移趋于一致。
特别地，当 t = 1 时：
v = (0.02 × θ) / (1 0.98) = θ
即实现了完全修正，使第一天的结果直接等于真实观测值。
京公网安备 11010802022788号
