ACMMM 2025 | 多变量时序分析新突破：Foresail实现LLM知识与深度网络的协同优化！

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

在医疗、金融等多个关键领域，多变量时间序列数据的分析至关重要。这类数据通常来自多个传感器，传统分析方法主要聚焦于数值本身的变化趋势，却往往忽视了传感器所携带的丰富背景信息——例如，某些指标同时出现异常可能暗示特定的系统故障或健康问题。虽然大型语言模型（Large Language Models, LLMs）具备获取此类知识的能力，但直接使用它们不仅计算开销大，还容易因“幻觉”现象导致推理结果不可靠，成为实际应用中的一大障碍。

针对这一挑战，本文提出了一种名为Foresail的新框架，通过构建一个状态引导网络，将LLM中的先验知识系统化地注入到现有的时间序列分类模型中。该方法不仅显著提升了分类准确率，还能生成具有可解释性的中间状态表示，增强了模型的透明性与实用性。

一、论文基本信息

• 论文标题：Foresail: LLM Sensor Knowledge Empowered Status-guided Network for Multivariate Time-series Classification
• 作者：Yuhan Jing, Bo He, Haifeng Sun, Qi Qi, Zirui Zhuang, Lei Zhang, Jianxin Liao, Jingyu Wang
• 论文链接：https://doi.org/10.1145/3746027.3755806
• 代码地址：https://github.com/weatherjyh/Foresail

二、核心贡献与创新点

• 设计了状态引导网络结构，能够高效且可扩展地将LLM提取的传感器知识显式整合进现有模型架构中。
• 提出一种数据驱动的不确定性学习机制，用于识别并修正LLM输出中的知识偏差和幻觉问题，提升知识融合的可靠性。
• 利用LLM的零样本（zero-shot）推理能力自动生成细粒度的状态标签，使模型能够学习到可解释的传感器行为模式。

三、方法架构与实现原理

Foresail的核心思想是：从LLM中提取关于传感器行为的先验知识，并通过一个专门设计的状态引导网络对这些知识进行建模与融合，从而增强多变量时间序列分类模型的表现力。

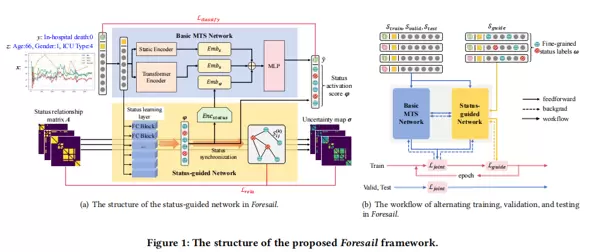
1. 从LLM中提取传感器先验知识

Foresail依赖于两种从LLM中提取的关键知识形式：状态关系矩阵和细粒度状态标签。研究者首先定义一组描述传感器状态的关键词，如“显著异常”、“逐渐恶化”等，作为语义锚点。

(1) 构建状态关系矩阵 (A)

为了揭示不同传感器之间的潜在关联，研究者设计了一个关系提取函数 F_rela^(k)，通过向LLM发送提示（prompt），询问哪些传感器倾向于在某一特定状态下共同异常（例如：“请将以下指标分组，同一组中的指标通常会同时出现异常：…”）。LLM返回自然语言形式的分组建议。

LLM关系搜索器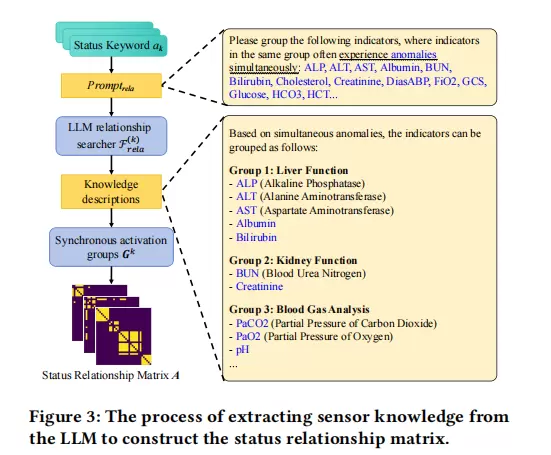

该过程的形式化表达如下：

G^(k) = {G₁^(k), G₂^(k), …} ← F_rela^(k) = LLM(Prompt_rela(s, a_k))

其中，s 表示所有传感器的集合，a_k 是第 k 个状态关键词，G^(k) 是LLM返回的分组结果。若两个传感器 s_i 和 s_j 被归入同一组，则认为它们在状态 a_k 下存在同步激活关系，此时状态关系矩阵 A 中对应位置 A_ij^(k) 设为1，否则为0。最终得到的张量 A ∈ ^K×N×N 编码了 N 个传感器在 K 种状态下的全局依赖结构。

(2) 生成细粒度状态标签 (ω)

为了使模型能理解每个传感器在具体样本中的动态状态，研究者利用LLM的零样本预测能力，设计了前视函数 F_fore^(k)。通过构造精细提示（如“传感器X的读数是否表现出‘显著异常’？”），让LLM判断某传感器在给定样本中是否激活了某个状态关键词。

LLM预测器

该流程可表示为：

F_fore^(k) = LLM{ LLM(Prompt_ref) + Prompt_fore(s_i, a_k) }

由此生成的标签 ω 提供了对传感器行为的细粒度语义标注，为后续模型训练提供了可解释监督信号。

大型语言模型 (LLMs)

在Foresail框架中，前向预测函数 \(\mathcal{F}^{(k)}_{fore}\) 由大语言模型（LLM）构建，其形式为：

\[ \mathcal{F}^{(k)}_{fore} = LLM\{LLM(Prompt_{ref}) + Prompt_{fore}(s_i, a_k)\} \]

该函数用于判断传感器 \(s_i\) 在状态关键词 \(a_k\) 下的行为倾向。结合样本的静态特征 \(\boldsymbol{z}\) 和时间序列输入 \(\boldsymbol{x}_i\)，可得状态权重：

\[ \omega^{(k)}_i \leftarrow \mathcal{F}^{(k)}_{fore}(\boldsymbol{x}_i, \boldsymbol{z}) \]

Prompt

其中，\(\boldsymbol{z}\) 表示样本的静态属性，\(\boldsymbol{x}_i\) 代表第 \(i\) 个传感器的时间序列数据。LLM输出的回答（如“是”或“否”）被解析为二值化的细粒度标签 \(\omega_i^{(k)} \in \{0,1\}\)，这些标签构成一个小规模但高信息密度的指导数据集，用于后续监督学习过程。

状态引导网络设计

作为Foresail的核心组件，状态引导网络负责从LLM提取的知识中进行建模，并将其融合进多变量时间序列（MTS）分析流程中。

1. 状态嵌入生成与融合机制

对于每个传感器的输入 \(\boldsymbol{x}_i\)，通过一个全连接块（FCBlock）计算其对各个状态关键词 \(a_k\) 的响应强度，得到状态激活分数向量：

\[ \boldsymbol{\chi}_i = \{\varphi^{(1)}_i, \varphi^{(2)}_i, \dots, \varphi^{(K)}_i\} \]

具体实现采用Sigmoid激活函数，并引入传感器掩码以过滤无效关联：

\[ \boldsymbol{\chi}_i = \text{Sigmoid}(\text{FCBlock}_i(\boldsymbol{x}_i)) \cdot mask(s_i) \]

所有传感器的状态激活结果 \(\boldsymbol{\chi}_1, \boldsymbol{\chi}_2, \dots, \boldsymbol{\chi}_N\) 被拼接后送入编码器模块，生成统一的状态嵌入表示 \(\boldsymbol{Emb}_{\varphi}\)：

\[ \boldsymbol{Emb}_{\varphi} = Enc_{status}(\boldsymbol{\chi}_1 \oplus \boldsymbol{\chi}_2 \oplus \cdots \oplus \boldsymbol{\chi}_N) \]

多层感知机 (multilayer perceptron, MLP)

最终，该状态嵌入与原始MTS模型中的静态特征嵌入 \(\boldsymbol{Emb}_z\)、时序特征嵌入 \(\boldsymbol{Emb}_x\) 进行拼接，共同输入分类头进行预测：

\[ \hat{y} = \text{MLP}(\boldsymbol{Emb}_z \oplus \boldsymbol{Emb}_x \oplus \boldsymbol{Emb}_{\varphi}) \]

Transformer

2. 状态关系的不确定性建模

考虑到LLM可能产生“幻觉”或错误关联，Foresail不盲目信任其提供的关系矩阵 \(\boldsymbol{A}\)，而是引入一种基于吉布斯分布的不确定性学习机制。每条潜在的关系 \(A_{ij}^{(k)}\) 被视为随机变量，其概率分布定义如下：

\[ p(\hat{A}^{(k)}_{ij} \mid S^{(k)}_{ij}, \sigma^{(k)}_{ij}) = \text{Softmax}\left( \frac{1}{(\sigma^{(k)}_{ij})^2} S^{(k)}_{ij} \right) \]

其中，\(S_{ij}^{(k)}\) 是基于内部状态激活得分 \(\varphi\) 计算出的同步性评分；\(\sigma_{ij}^{(k)}\) 为可学习的不确定性参数——数值越大，表明该关系越不可靠，在训练过程中所占损失权重越低。

整体的状态关系损失 \(\mathcal{L}_{rela}\) 采用负对数似然近似，表达式为：

\[ \mathcal{L}_{rela} \approx \sum_k \sum_i \sum_j \left( \frac{1}{(\sigma_{ij}^{(k)})^2} \right) \]

这一机制有效缓解了LLM噪声带来的负面影响，增强了模型鲁棒性。

在多变量时间序列分类任务中，Foresail提出了一种新颖的损失函数设计：

\[ \mathcal{L}_{rela} \approx \sum_k \sum_i \sum_j \left( \frac{1}{(\sigma^{(k)}_{ij})^2}(\mathcal{L}_{CE}(A^{(k)}_{ij}, S^{(k)}_{ij}) + \log \sigma^{(k)}_{ij}) \right) \cdot A^{(k)}_{ij} \]

其中，\(\mathcal{L}_{CE}\) 表示交叉熵损失（cross entropy loss）。该损失结构具有双重作用：一方面推动模型拟合来自大型语言模型（LLM）的知识（即最小化 \(\mathcal{L}_{CE}\)），另一方面促使模型学习评估这些知识的可信度，通过动态调整不确定性参数 \(\sigma^{(k)}_{ij}\) 实现对先验信息可靠性的建模。

交替训练策略

为了有效融合不同类型的学习信号，Foresail采用交替优化机制。整体训练使用联合损失函数：

\[ \mathcal{L}_{joint} = \mathcal{L}_{rela} + \mathcal{L}_{classify} \]

该目标同时优化关系学习与主分类任务。此外，在一个小型但语义丰富的指导数据集上，引入额外的监督信号——指导损失：

\[ \mathcal{L}_{guide} = \sum_{i,k} \mathcal{L}_{CE}(\omega^{(k)}_i, \varphi^{(k)}_i) \]

此损失用于对齐模型内部学习到的状态激活分数与LLM生成的细粒度标签，确保所学状态具备明确且可解释的物理含义。

实验设计与结果分析

为全面验证Foresail的有效性，实验选取了五个公开数据集进行测试，包括P12、P19和HumanActivity（不规则采样），以及FingerMovements和NATOPS（规则采样）。评价指标涵盖准确率（Acc）、精确率-召回率曲线下面积（AUPRC）、ROC曲线下面积（AUROC）以及F1分数。

对比实验

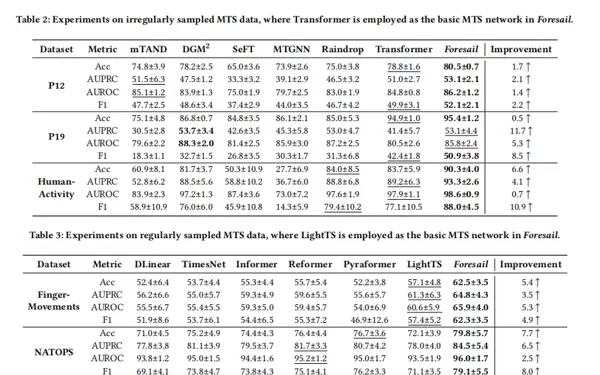
实验结果显示，无论在规则还是不规则采样场景下，Foresail在所有基线模型中表现最优，尤其在F1分数上优势显著。例如，在P19数据集上，相比基础Transformer架构，Foresail实现了8.5%的F1提升；而在HumanActivity数据集中，性能增幅达到10.9%。这表明，通过系统性地整合LLM中的先验知识，Foresail能够挖掘出传统方法难以捕捉的深层语义特征，从而显著增强分类能力。

可视化对比

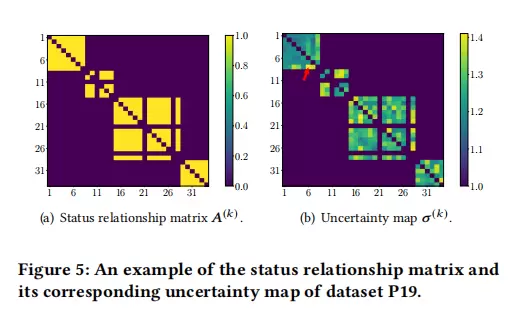
为进一步验证不确定性建模的效果，研究对状态关系矩阵 \(\boldsymbol{A}\) 与学习得到的不确定性图 \(\boldsymbol{\sigma}\) 进行了可视化分析。在一个具体案例中，对于LLM建议但实际关联较弱的两个变量（如DBP与EtCO2），模型自动赋予了很高的不确定性值。这一现象说明，Foresail具备识别并抑制LLM“幻觉”或噪声信息的能力，提升了整体推理的鲁棒性。

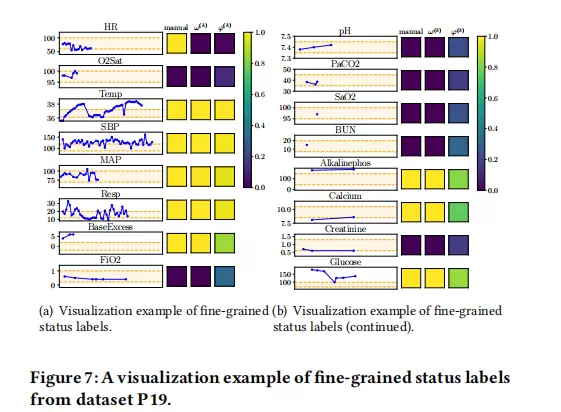
同时，论文还展示了传感器原始读数、LLM预测的细粒度状态标签以及模型输出的状态激活分数之间的对应关系。结果表明，LLM的零样本预测与基于医学常识的人工判断高度一致，而模型学习到的激活模式也与LLM标签保持良好对齐。这不仅证明了性能增益的来源，更揭示了Foresail生成过程的透明性和可解释性。

消融实验

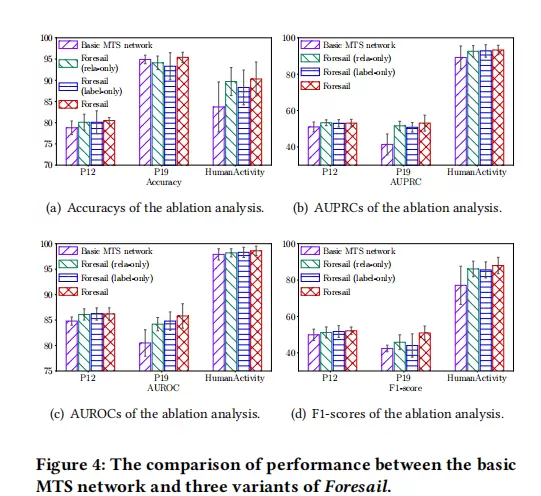
通过消融研究进一步剖析各模块贡献。单独启用关系学习（Foresail (rela-only)）或仅使用细粒度标签指导（Foresail (label-only)）均能带来性能提升，但完整模型效果最佳。这说明，关系层面的知识（描述变量间联系）与状态层面的知识（描述单个变量行为）是互补的，二者从不同角度提供先验信息，协同优化使模型达到最优表现。

结论与评价

Foresail是一项将大型语言模型中的自然语言先验知识与深度神经网络深度融合的创新尝试。其实验证明，该框架不仅能显著提升多变量时间序列分类的性能，还能借助不确定性学习机制有效过滤LLM可能引入的错误或误导性信息。这种结合方式为复杂数据分析任务中如何合理利用LLM提供了清晰、可行的技术路径，具有较强的推广价值和研究启发意义。

主要优点

• 框架设计具有高度创新性，适用于多种时间序列场景
• 实现LLM知识与深度模型的有机融合，兼顾性能与可解释性
• 引入不确定性建模机制，增强对LLM“幻觉”的鲁棒性
• 训练策略灵活，支持多阶段、多目标联合优化

Foresail 具备高度模块化的设计特点，能够以“插件”形式无缝集成到多种现有的 MTS 网络中，显著提升系统性能，展现出广泛的应用潜力。

可解释性强：

通过可视化展示状态激活分数与不确定性图谱，模型摆脱了传统“黑箱”模式。研究人员可以清晰地观察模型如何判断传感器状态，并了解其对来自大语言模型（LLM）知识的信任程度，从而增强理解与调试能力。

鲁棒性设计：

该框架创新性地引入了不确定性学习机制，主动对 LLM 提供知识的不可靠性进行建模与量化。这一设计在真实应用场景中尤为关键，有效提升了模型运行的稳定性与整体可靠性。

缺点分析：

依赖于 LLM 的性能：

模型的整体表现受限于所选用的大语言模型的知识覆盖范围及其推理水平。实验结果显示，更换不同 LLM 会显著影响最终效果，说明该框架的性能与 LLM 的发展水平密切相关。

关键词定义的主观性：

模型所依赖的“状态关键词”需根据具体任务由人工设定，这一过程不仅需要一定的领域专业知识，还可能因人而异，导致关键词集合存在差异，进而对模型的标准化部署和跨场景复用带来挑战。

知识提取的开销：

虽然在推理阶段无需直接调用 LLM，但在训练前需从 LLM 中提取知识——尤其是生成细粒度标签的过程——仍需消耗较多计算资源与时间。当面对大规模传感器网络或海量样本时，这一预处理步骤的成本尤为突出。

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：RES ACM 多变量 LLM cmm