基于MATLAB的三段式电流保护仿真实践
最近在进行继电保护相关的仿真工作,发现使用MATLAB实现三段式电流保护非常适合初学者上手。本文不深入理论推导和公式讲解,而是聚焦于实际操作,通过代码演示如何设置参数、分析动作特性,并配有实测视频供参考,确保你能顺利复现整个过程。
第一段保护:电流速断
一段保护的核心原理是快速切除故障,属于无时限电流速断。其整定计算的关键在于两个方面:一是躲过本线路末端最大短路电流;二是保证足够的灵敏度。在利用MATLAB进行整定值计算时,必须充分考虑系统不同的运行方式对结果的影响。
具体实现中,需要注意一个常见问题:当系统等效阻抗变化超过20%时,原有的速断定值可能失去选择性,导致误动或拒动。因此,在实际工程中通常需要配合自动重合闸功能来提升可靠性。相关动作逻辑与异常情况将在配套视频中详细展示。
% 一段保护整定
I_k_max = 12.5e3; % 最大运行方式下三相短路电流
K_rel = 1.3; % 可靠系数
I_op1 = K_rel * I_k_max;
disp(['一段整定值: ', num2str(I_op1/1e3), 'kA']);第二段保护:限时电流速断
二段保护的设计难点在于与相邻线路保护的时间配合。为了实现选择性,需采用时间阶梯原则进行整定。以下是一个实用的时间级差计算模板:
其中关键点在于max函数的应用——既要确保动作电流低于下一级线路一段保护的定值,又要满足本段保护的灵敏度要求。这两个条件有时会相互冲突,一旦出现矛盾,就需要回溯重新评估系统短路容量及网络结构参数。
% 二段时限整定
t_step = 0.5; % 时间级差
t_prev = 1.2; % 相邻线路一段动作时间
t_op2 = t_prev + t_step;
% 电流整定(以最小方式短路电流为基准)
I_k_min = 8.2e3;
K_sen = 1.5; % 灵敏系数
I_op2 = max(I_op1/1.1, I_k_min/K_sen);
fprintf('二段整定: %.2fkA @ %.1fs\n', I_op2/1e3, t_op2);第三段保护:过电流保护
三段保护主要用于后备保护,但最容易受到负荷电流干扰。例如下面这种未加判据的情况:
当负荷电流较大时,保护可能误判为故障电流而误动作。解决该问题的有效方法是引入复合电压闭锁机制,在原有电流判据基础上增加低电压条件判断。加入电压闭锁后,可显著提高动作的选择性和可靠性。
视频中展示了添加闭锁前后的动作区域对比,效果非常明显,能够清晰看出保护范围的变化与抗干扰能力的提升。
% 错误的三段整定示例
I_load = 950; % 负荷电流
I_op3 = 1.2 * I_load; % 按常规1.2倍整定
I_k_min = 800; % 远端最小短路电流
if I_op3 > I_k_min
warning('三段保护可能拒动!需要校核灵敏度')
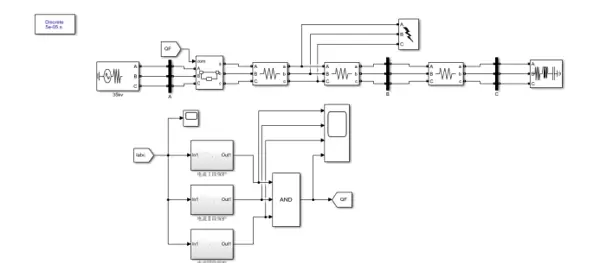
end仿真架构与核心模块设计
整个仿真系统基于Simulink搭建,保护逻辑以模块化形式实现。其中最关键的部分是比较器与延时动作单元的配置。
特别值得一提的是持续计时器的设计,它真实模拟了传统继电器的积分式动作行为。通过合理使用persistent变量,避免了全局变量带来的数据污染问题,同时提升了代码的封装性和可读性。
在测试阶段,共模拟了三种典型故障场景:区外故障转区内故障、发展性多点故障以及CT饱和条件下的采样失真情况。观察保护动作序列时,应重点关注二段保护的返回系数设置——若该参数不合理,极易引发越级跳闸事故,这一点我在调试过程中曾亲身经历。
function [trip] = RelayLogic(I_meas, I_set, t_delay)
persistent timer;
if isempty(timer)
timer = 0;
end
if I_meas > I_set
timer = timer + 0.001; % 仿真步长1ms
else
timer = 0;
end
trip = (timer >= t_delay);
end结语
本期内容围绕三段式电流保护在MATLAB环境下的建模与调试展开,重点讲解了各段保护的整定思路、常见问题及解决方案。后续将推出关于距离保护的专题分享,特别是如何准确绘制多边形动作特性曲线,敬请期待。




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







