发帖
雷达卡
锂电池SOC估计看似简单，但在实际应用中却充满挑战。本文基于二阶RC等效电路模型，结合扩展卡尔曼滤波（EKF）方法，对SOC进行估算，并在HPPC工况与1C恒流放电工况下进行了验证。
首先来看模型结构。采用的二阶RC模型包含两个并联的电阻-电容支路，能够更准确地反映电池在动态过程中的极化行为，相较于一阶模型具有更强的动态响应模拟能力。这种结构尤其适用于捕捉复杂电流变化下的电压响应特性。
为了实现EKF算法，必须将系统的连续状态方程进行离散化处理。核心部分体现在predict_state函数中，其负责更新SOC以及两个极化电压的状态量：
def predict_state(soc, v1, v2, current, dt, R1, C1, R2, C2):
soc_new = soc - dt/(3600*capacity) * current
v1_new = np.exp(-dt/(R1*C1)) * v1 + R1*(1 - np.exp(-dt/(R1*C1))) * current
v2_new = np.exp(-dt/(R2*C2)) * v2 + R2*(1 - np.exp(-dt/(R2*C2))) * current
return soc_new, v1_new, v2_new上述代码段虽简洁，但关键在于指数衰减项的时间常数计算。其中R1C1和R2C2作为重要的动态参数，若未经过精确辨识，会导致状态预测失准，进而严重影响整体估计精度。
在EKF算法中，雅可比矩阵的构建至关重要，尤其是OCV-SOC关系曲线的偏导数计算。实践表明，使用样条插值（spline）比传统多项式拟合更能稳定反映非线性变化趋势：
from scipy.interpolate import UnivariateSpline
ocv_spline = UnivariateSpline(soc_data, ocv_data, s=0)
dOCV_dSOC = ocv_spline.derivative()以某款三元锂电池为例，在SOC约为30%时，dOCV/dSOC斜率可达80mV/%，属于高敏感区域，此时EKF能有效利用电压变化信息提升收敛速度。然而当SOC进入50%附近的电压平台区时，开路电压变化微弱，导致卡尔曼增益显著降低，滤波器对外部观测依赖减弱，此时模型本身的准确性成为决定因素。
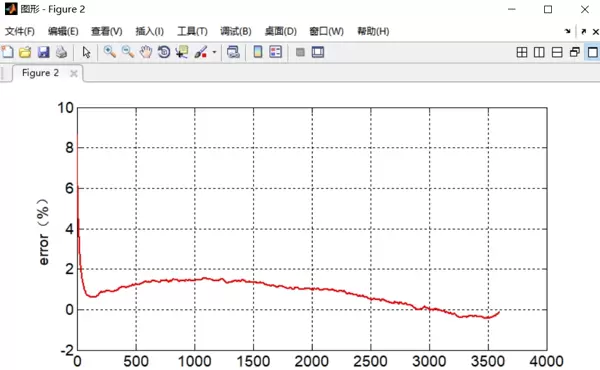
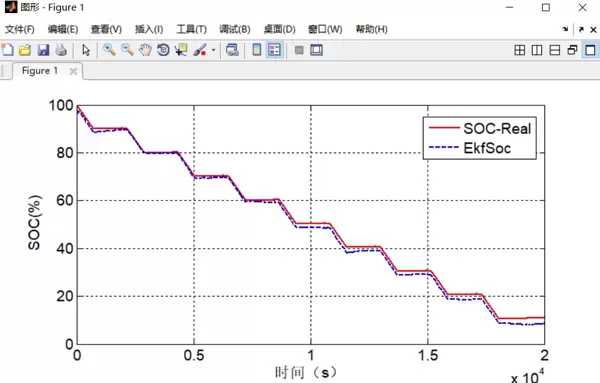
在HPPC测试工况下的实验结果揭示了一个反直觉现象：脉冲放电阶段的SOC估计误差反而小于静置阶段。深入分析协方差矩阵演化过程后发现，频繁的电流变动实际上增强了系统可观测性，提供了更多可用于修正状态的信息。相反，在1C恒流放电过程中，由于电流持续且变化小，误差会随时间缓慢累积，呈现出“温水煮青蛙”式的漂移效应。为此，引入自适应调整过程噪声协方差的方法可有效缓解该问题。
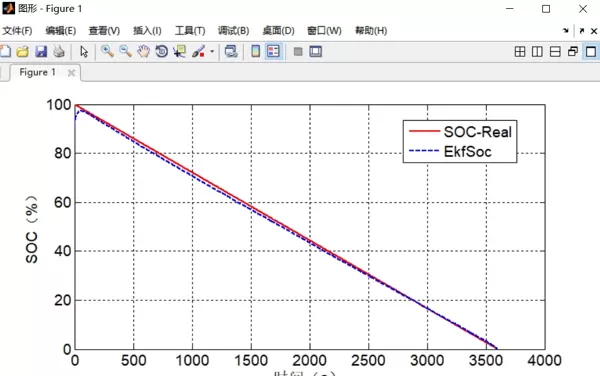
最后给出几点工程建议：与其过度纠结EKF内部参数调优，不如优先确保HPPC测试数据的质量。通过建立SOC与模型参数之间的二维查表关系，考虑参数随荷电状态的变化趋势，可使估计精度提升至少3%。此外，测量噪声协方差矩阵不宜设置过小，应预留足够裕度以应对BMS现场采集环境中存在的电流波动和传感器误差，毕竟车载条件远不如实验室理想。
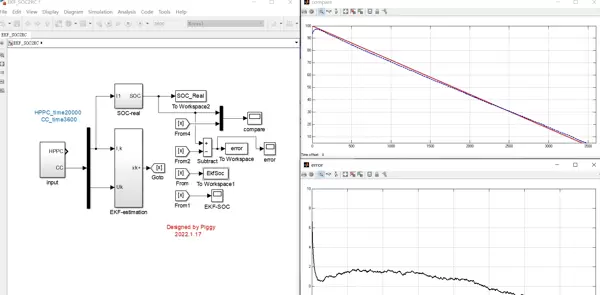
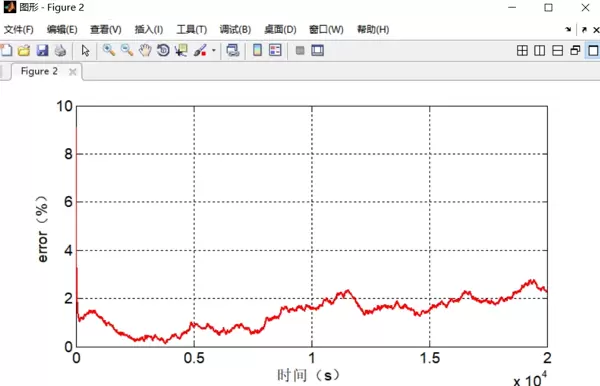
整体方案验证流程如下图所示：
京公网安备 11010802022788号
