4. 机器学习 - 逻辑回归
1)基本概念
逻辑回归(Logistic Regression) 是一种监督学习算法,主要用于解决分类问题,尤其在二分类任务中表现突出。例如判断一封邮件是否为垃圾邮件、用户是否会点击广告等场景。虽然名称中含有“回归”二字,但实际上它属于分类方法,而非回归分析。
2)核心原理与优势
该模型通过引入 S 型函数——即 Sigmoid 函数,将线性组合的输出压缩到 [0, 1] 区间内,表示样本属于正类的概率。

结果判定规则: 若预测概率大于 0.5,则判定为正类;否则归为负类。
主要优点包括:
- 可解释性强: 每个特征对应的权重系数可以直接反映其对预测结果的影响方向和程度。
- 计算效率高: 训练和推理速度快,适合处理大规模数据集。
- 基础性显著: 是许多高级模型(如神经网络)中的基本构成单元。
- 输出概率值: 不仅给出类别标签,还提供置信度信息,有助于后续决策流程。
- 适用于线性可分数据: 当特征与类别之间存在近似线性关系时,模型性能优异。
典型应用示例: 在金融风控领域,银行可以利用客户的收入水平、信用评分等变量,使用逻辑回归预测其违约风险。
4.1 Sigmoid 函数详解
Sigmoid 函数是逻辑回归的关键组件,能够将任意实数映射至 (0, 1) 范围内,用以表示事件发生的概率。
数学表达式如下:

特性说明:
- 输出始终介于 0 和 1 之间;
- 当输入 z 趋向正无穷时,函数值趋近于 1;当 z 趋向负无穷时,函数值趋近于 0;
- 整体呈“S”形曲线,连续且光滑,便于求导,有利于优化过程。
可视化示意:
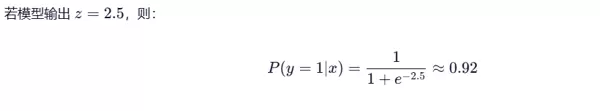
注:尽管常用 Sigmoid,但在多分类扩展中也可采用其他激活函数,如 Softmax。
4.2 参数优化方法
逻辑回归的目标是寻找最优参数 β,使得模型预测尽可能准确。常用的两种优化策略如下:
4.2.1 极大似然估计
该方法基于伯努利分布假设,目标是最大化所有样本联合出现的概率,也就是最大化似然函数。
数学形式表达:
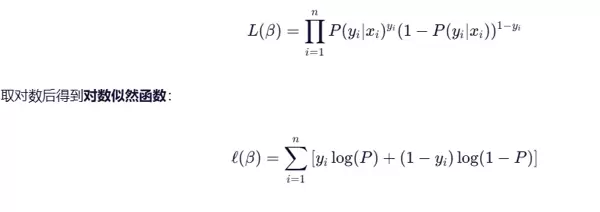
在实际操作中,通常转化为最小化负对数似然,这等价于最小化损失函数。
4.2.2 最小化交叉熵损失
交叉熵损失是极大似然估计的另一种等效形式,广泛应用于分类任务及深度学习中。
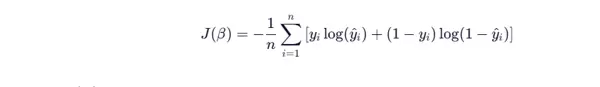
优化目标: 使用梯度下降法迭代更新参数,持续降低损失函数值。
梯度计算公式:
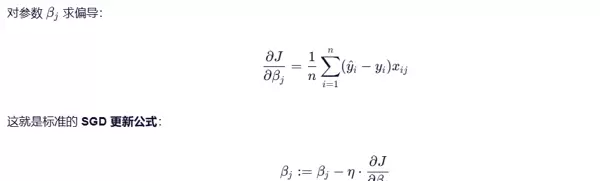
总结: 逻辑回归的本质是结合了 Sigmoid 映射、交叉熵损失函数以及梯度下降优化策略的一种建模方式。
3)适用场景
以下情况推荐使用逻辑回归:
- 二分类任务: 如疾病诊断(患病/健康)、垃圾邮件识别、点击率预估等。
- 特征与目标呈近似线性关系: 数据可用直线或超平面较好分离。
- 强调模型可解释性: 医疗、金融等行业需要清晰解释判断依据。
- 中等维度但数据量较大: 适用于结构化数据的大规模训练。
- 作为基准模型: 常用于对比更复杂模型(如随机森林、XGBoost)的效果。
实际案例: 电商平台可根据用户的浏览时长、历史购买记录等特征,构建逻辑回归模型预测其是否会下单。
4)不适用情形
尽管逻辑回归有诸多优点,但在以下场景应谨慎使用或避免:
- 非线性关系明显: 如数据分布呈环形边界或异或结构,逻辑回归难以捕捉复杂模式。
- 原生不支持多分类: 需借助 One-vs-Rest 或 Softmax 才能扩展至多类问题。
- 多重共线性严重: 特征高度相关会导致参数估计不稳定,影响解读可靠性。
- 样本量极小: 尽管对小数据有一定适应能力,但过少样本易导致过拟合。
- 追求高精度且特征复杂: 相较于随机森林、XGBoost 或深度学习模型,逻辑回归精度相对有限。
举例说明: 图像识别任务(如人脸识别)不适合采用逻辑回归,因像素点之间的关系高度非线性,无法通过线性模型有效建模。
4.3 混淆矩阵(关键评估工具)
混淆矩阵是衡量分类模型性能的重要手段,尤其在类别不平衡的数据集中更具参考价值。
| 预测为正类 | 预测为负类 | |
|---|---|---|
| 实际为正类 | TP(真阳性) | FN(假阴性) |
| 实际为负类 | FP(假阳性) | TN(真阴性) |
术语解释:
- TP(True Positive): 正确识别为正类,如真正患病者被检出。
- FP(False Positive): 错误标记为正类,如健康人被误诊为患者。
- FN(False Negative): 漏判正类,如病人未被发现。
- TN(True Negative): 正确识别为负类,如健康人正确排除。
关注重点依场景而定:
- 医疗诊断中更重视减少 FN,防止漏诊;
- 广告投放中更关注控制 FP,避免预算浪费。
提示:可通过 sklearn.metrics.confusion_matrix() 快速生成混淆矩阵。
4.4 分类模型评估指标(重要)
基于混淆矩阵,可进一步计算多种评估指标,用于全面评价模型表现:
- 准确率(Accuracy): (TP + TN) / 总样本数
- 精确率(Precision): TP / (TP + FP),反映预测为正类的准确性
- 召回率(Recall/Sensitivity): TP / (TP + FN),体现发现正类的能力
- F1 分数: 精确率与召回率的调和平均,平衡二者矛盾
- 特异性(Specificity): TN / (TN + FP),衡量负类识别能力
5)总结归纳
| 项目 | 内容 |
|---|---|
| 核心用途 | 解决二分类问题建模 |
| 优点 | 结构简单、运行高效、具备良好可解释性,输出结果为概率形式 |
| 缺点 | 依赖线性假设、难以处理非线性关系、对异常值较为敏感 |
| 典型应用场景 | 风险评估、市场营销、医学诊断等领域 |
| 替代方案 | 支持向量机(SVM)、决策树、随机森林、神经网络等 |
一句话概括: 逻辑回归是机器学习中最基础且实用的分类算法之一,特别适用于需要快速部署和结果透明可解释的应用场景。虽然不能应对所有复杂问题,但在合适的条件下,它是一种简洁而高效的解决方案。
针对不同的业务场景,选择合适的评估指标至关重要。以下是几种常见的分类模型评价指标及其特点与应用场景:
4.4.1 准确率(Accuracy)
准确率衡量的是模型在所有预测样本中判断正确的比例,计算方式为正确预测的总数除以总样本数。
优点:
直观易懂,能够快速反映模型的整体预测效果。
缺点:
当数据类别分布极度不均衡时,准确率会严重失真。例如,在负类占99%、正类仅占1%的数据集中,即使模型将所有样本都预测为负类,也能达到99%的准确率。
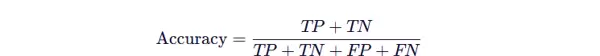
注意:在类别严重不平衡的情况下,不建议单独使用准确率作为评估标准。
4.4.2 精确率(Precision)
精确率关注的是:在被模型预测为正类的样本中,实际为正类的比例。
它强调“预测结果的可靠性”,即尽量减少误报(False Positive)。
典型应用:
如垃圾邮件识别系统,需避免将正常邮件错误归类为垃圾邮件,因此要求高精确率。
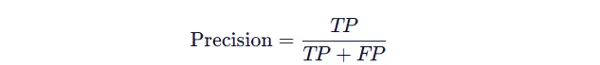
4.4.3 召回率(Recall)
召回率反映的是:在真实为正类的所有样本中,模型成功识别出的比例。
其核心在于“是否遗漏关键样本”,重视降低漏检(False Negative)。
适用场景:
例如医学疾病筛查,宁可多预警几次,也不能漏掉一个真正患者,因此需要高召回率。
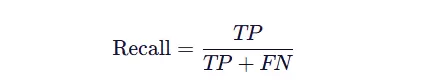
4.4.4 F1-score
F1-score 是精确率和召回率的调和平均值,用于综合平衡二者之间的关系。
优点:
当其中一个指标偏低时,F1值会显著下降,能有效揭示模型在两项指标上的失衡问题。
使用建议:
适用于对精确率和召回率均有较高要求的任务,如信息检索、推荐系统等。

4.4.5 ROC曲线
ROC曲线通过绘制不同分类阈值下的真正率(TPR)与假正率(FPR)来展示模型性能。
横轴: 假正率(FPR)
纵轴: 真正率(TPR)
绘制方法:
调整分类阈值从0到1变化,计算每个点对应的TPR和FPR,并连接成曲线。

图中蓝色线代表模型表现,红色虚线表示随机猜测水平(AUC=0.5)。理想情况下,模型曲线应尽可能远离对角线,靠近左上角。
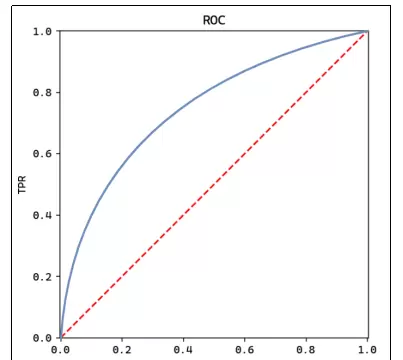
解读要点:
- 曲线越接近左上角,模型性能越好;
- 对角线对应随机分类器(AUC = 0.5);
- 完美分类器的AUC为1。
4.4.6 AUC面积
AUC指ROC曲线下的面积,取值范围为[0, 1],反映模型对正负样本的排序能力。
意义:
AUC越大,说明模型越有能力将正类排在负类之前;且该指标不依赖具体分类阈值,适合跨模型比较。
| AUC值 | 解读 |
|---|---|
| < 0.5 | 模型表现不如随机猜测 |
| 0.5–0.7 | 性能较弱 |
| 0.7–0.8 | 中等水平 |
| 0.8–0.9 | 表现良好 |
| > 0.9 | 性能优秀 |
总结对比表
| 指标 | 公式 | 关注重点 | 适用场景 |
|---|---|---|---|
| 准确率 | (TP+TN)/全部 | 整体正确率 | 类别分布均衡的数据集 |
| 精确率 | TP/(TP+FP) | 预测为正类的准确性 | 需控制误报的场景(如广告投放) |
| 召回率 | TP/(TP+FN) | 找出所有正类的能力 | 需避免漏报的场景(如疾病检测) |
| F1-score | 2×P×R/(P+R) | 平衡精确率与召回率 | 两者均重要的任务 |
| ROC/AUC | 曲线下方面积 | 模型整体排序能力 | 多模型对比或阈值不固定时 |
一句话总结:
尽管逻辑回归结构简单,但其背后的Sigmoid函数、最大似然估计(MLE)、交叉熵损失等数学原理,以及基于混淆矩阵、F1-score、AUC等构成的评估体系,共同搭建了现代分类建模的核心框架。深入理解这些内容,是科学选择、训练与评估分类模型的基础。




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







