基于一致性理论的多智能体编队控制论文复现
在多智能体系统研究中,编队控制是实现协同运动的重要课题。该技术旨在让多个智能体通过局部信息交互,自主调整行为以维持预设的几何队形。利用一致性理论作为控制基础,能够有效解决此类协同问题。本文将介绍如何使用 MATLAB 实现相关算法,并对关键代码段进行解析。
一致性理论的核心思想
一致性理论关注的是网络化智能体如何通过邻居间的状态交换,逐步收敛到统一的状态值。在编队控制中,这一机制被用于调节各智能体的位置与速度,使其最终形成并保持期望的队列结构。每个个体仅依赖与其相连的邻居信息进行更新,无需全局控制器介入,体现出良好的分布式特性。
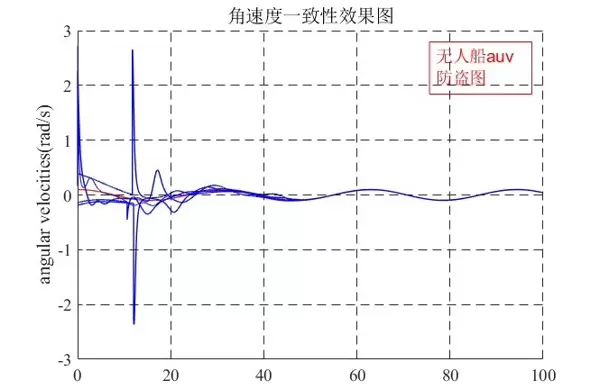
MATLAB 编程实现流程
以下为基于一致性协议设计的多智能体编队控制仿真代码框架。程序主要包括参数初始化、迭代更新和动态可视化三个部分。
参数设置阶段
- 智能体数量设定:本例中设为5个智能体,可根据实际需求修改。
numAgents - 时间步长选择:采用固定时间步长以保证数值稳定性,较小的步长提升精度但增加计算负担。
dt - 总仿真时长:定义整个运行过程的时间跨度,确保系统有足够时间达到稳态。
simTime - 初始位置生成:通过随机函数在二维平面内初始化各智能体的空间坐标。
agentsPositionrand - 初始速度设定:所有智能体起始速度设为零向量,表示静止启动。
agentsVelocity - 通信拓扑配置:采用全连接结构,即任意两个智能体之间均可直接通信。此结构可后续替换为更复杂的稀疏图或切换拓扑。
communicationGraph
状态迭代更新逻辑
- 在每一时间步中,程序进入双重循环结构,计算每个智能体的一致性控制输入项。
t - 内层循环遍历所有其他智能体,若两者间存在通信链路(即拓扑矩阵对应元素非零),则累加其相对位置偏差。
communicationGraph(i, j) == 1ij - 根据累积的邻居位置差,按比例调整当前智能体的速度增量,再乘以时间步长完成速度更新。
neighborSum - 利用更新后的速度推进位置变化:新位置 = 原位置 + 速度 × 时间步长,实现状态演化。
动态图形展示
- 每一步迭代后调用绘图函数绘制当前所有智能体的位置点。
scatter - 通过清屏指令清除前一帧图像,重新绘制最新分布,形成连续动画效果,直观反映编队形成过程。
clf
参考文献资料
以下学术论文为本方法提供了坚实的理论支撑,建议深入阅读以掌握一致性算法的设计原理及其在网络化系统中的扩展应用:
- Olfati - Saber, R., & Murray, R. M. (2004). Consensus problems in networks of agents with switching topology and time - delayed communications. IEEE Transactions on Automatic Control, 49(9), 1520 - 1533.
- Ren, W., & Beard, R. W. (2005). Consensus seeking in multi - agent systems under dynamically changing interaction topologies. IEEE Transactions on Automatic Control, 50(5), 655 - 661.
总结
本文围绕基于一致性理论的多智能体编队控制展开,完成了从理论理解到 MATLAB 仿真实现的全过程复现。通过对核心代码的分段解释,帮助读者把握算法运行机制。希望该内容能为相关领域的学习与研究提供实用参考。
% 定义智能体数量
numAgents = 5;
% 定义时间步长
dt = 0.1;
% 定义仿真时间
simTime = 10;
% 初始化智能体位置
agentsPosition = rand(numAgents, 2);
% 初始化智能体速度
agentsVelocity = zeros(numAgents, 2);
% 定义通信拓扑,这里简单设为全连接
communicationGraph = ones(numAgents);
diag(communicationGraph) = 0;
for t = 0:dt:simTime
% 计算每个智能体的一致性控制输入
for i = 1:numAgents
neighborSum = zeros(1, 2);
for j = 1:numAgents
if communicationGraph(i, j) == 1
neighborSum = neighborSum + (agentsPosition(j, :) - agentsPosition(i, :));
end
end
% 根据一致性理论更新速度
agentsVelocity(i, :) = agentsVelocity(i, :) + dt * neighborSum;
end
% 更新智能体位置
agentsPosition = agentsPosition + dt * agentsVelocity;
% 绘图展示
figure(1);
clf;
scatter(agentsPosition(:, 1), agentsPosition(:, 2));
title(['Time: ', num2str(t)]);
xlabel('X Position');
ylabel('Y Position');
drawnow;
end



 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







