在浮点数运算中,当参与计算的数值存在较大数量级差异时,容易出现“大数吃小数”的现象。这种现象主要发生在大值域下的累加过程中,由于浮点数表示精度有限,较小的数值在与较大的数值相加时,可能因有效位被舍弃而无法对结果产生影响。
以 float32 类型为例,其可表示的最大值约为 3.40282347e+38。当两个数量级相差悬殊的数进行相加时,系统会优先保留大数的有效位数,导致小数部分的信息丢失。如下图所示,在不同累加顺序下(a+b+c 与 a+c+b),最终结果出现差异,这正是浮点数在高阶码区间内精度受限的表现。

案例分析:matmul 算子在 K 值极大场景下的精度问题定位
背景描述
该问题源自开源项目 ascend-transformer-boost 中的 matmul 测试用例:
https://gitcode.com/cann/ascend-transformer-boost/blob/master/tests/apitest/kernelstest/matmul/test_pp_matmul_accum.py
测试数据范围位于 [-5,5] 区间内,但在与 CPU 计算结果对比时,发现最大相对误差和最大绝对误差均超出预期标准。特别是 output[14984, 16986] 位置的结果未能满足相对误差 ≤ 2^(-7) 的要求。
@op_test.only_910b
def testcase_matmul_accum_atomic_fp16_nn(self):
bsize, msize, ksize, nsize = 1, 20090, 40192, 30208
ta, tb = False, True
self.set_param(
"MatMulOperation",
{
"transposeA": ta,
"transposeB": tb,
"oriShape": [msize, ksize, nsize],
"matmulType": MATMUL_ACCUM_ATOMIC,
},
)
self.set_input_formats([self.format_nd, self.format_nd, self.format_nd])
self.set_output_formats([self.format_nd])
self.__gen_test_data((bsize, msize, ksize, nsize), ta, tb, torch.float16)
self.execute(
[self.bat_A.half(), self.bat_B.half(), self.bat_C.float()],
[2],
)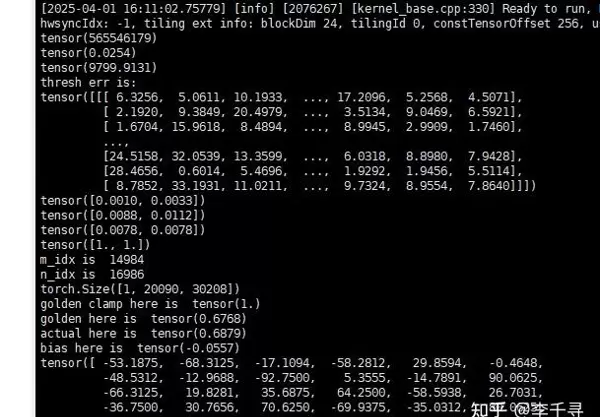
原因排查与分析
当前 matmul 算子采用 fp16 输入格式,基块划分参数为 m0=128、k0=256、n0=256。其中 k 维度进一步细分为 4 组,每组处理 64 个元素。具体计算流程如下:
- 首先在 K 方向上对每组 64 个元素执行 reduce 操作;
- 随后对 4 个组间结果再次 reduce;
- 最后通过原子加法完成各基块间的累加。
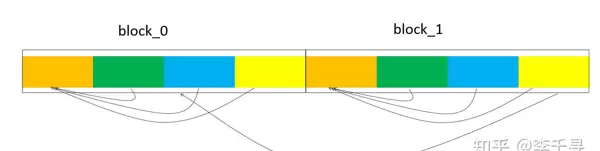
经核查,NPU 内部计算逻辑无误。将 [14984, 16986] 处的数据与其他正常精度位置的数据互换后,输出结果未发生变化,说明并非局部数据异常所致,基本排除了输入本身引发精度问题的可能性。
为进一步验证,将该数据移至矩阵其他位置进行测试:
置于 [0,0] 位置时的计算结果:
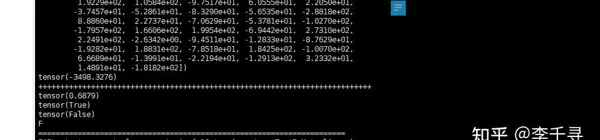
置于 [100,10] 位置时的计算结果:
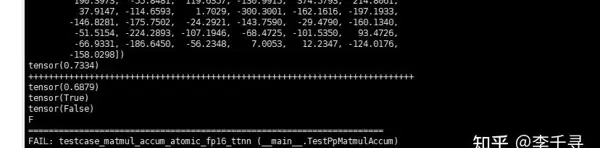
整体误差分布情况如下:
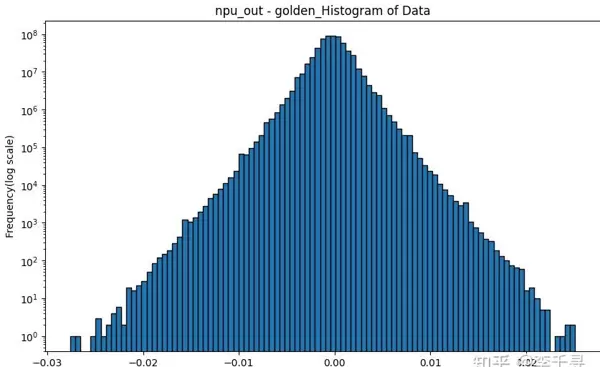
相对误差分布显示,最左侧的极值点是造成整体精度不达标的主要因素:
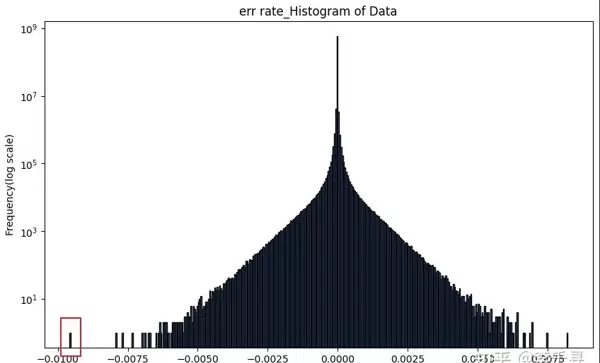
结论总结
NPU 与 CPU 在累加顺序上存在差异,尤其当 m、n、k 三个维度均较大时,某些特殊数值组合会在特定计算路径下被放大,从而导致最终精度不符合预期。根本原因在于浮点数累加过程中的“大数吃小数”效应,叠加不同的并行化 reduce 策略,使得结果偏离理论值。
附录:关于“大数吃小数”现象的技术解析
浮点数精度的本质机制
每个阶码对应一个固定的精度下限。在 IEEE 754 单精度(float32)格式中,阶码使用移码表示,尾数部分为 23 位,并采用规格化形式存储(隐含前导 1)。
例如,当阶码为 13(移码表示)时,其所能表示的最小精度单位由尾数位宽决定:


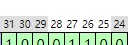


此时该阶码下的精度极限可计算如下:
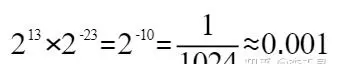
浮点数加法的五个核心步骤
- 对阶:调整两操作数的指数至相同,通常将较小指数向较大指数对齐,同时相应右移尾数以保持数值不变。
- 尾数相加:对齐后执行尾数加法运算。若结果超出表示范围,则需进行舍入并考虑进位到阶码。
- 规格化:确保尾数处于规范形式(即最高有效位为 1),必要时左右移动尾数并同步调整阶码。
- 舍入处理:遵循“最近偶数舍入”原则(Round to Nearest Even)。若结果恰处于两个可表示值中间,则选择最低有效位为偶数的那个。
- 溢出判断:检查阶码是否超出合法范围,如发生溢出则返回 ±∞ 或最大可表示数。
示例:
a = 8388609
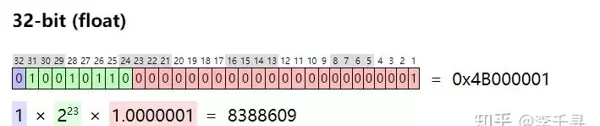
b = 8388608
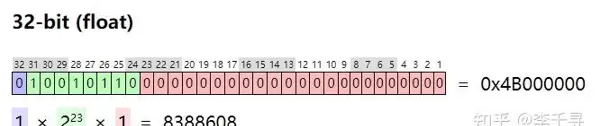
a + b = 16777217

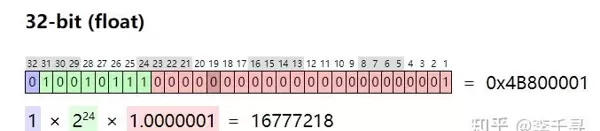
import numpy as np
a = np.float32(8388609)
b = np.float32(8388608)
a_fp64 = np.float64(8388609)
b_fp64 = np.float64(8388608)
print(type(a+b))
print(a+b)
print(type(a_fp64+b_fp64))
print(a_fp64+b_fp64)<class 'numpy.float32'>
16777216.0
<class 'numpy.float64'>
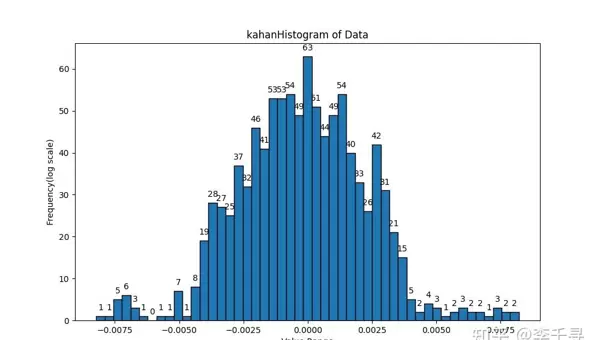
16777217.0不同累加顺序对精度影响的自测脚本验证
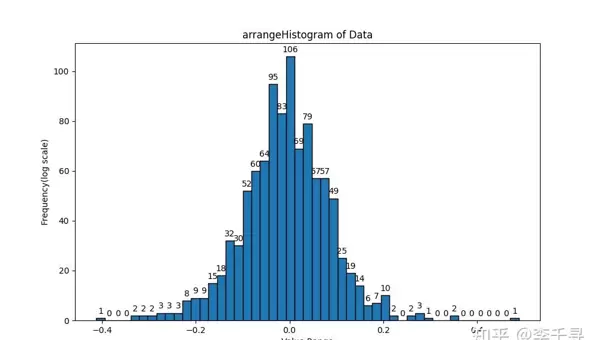
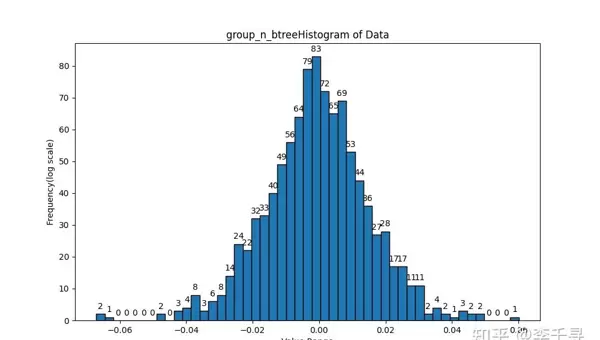
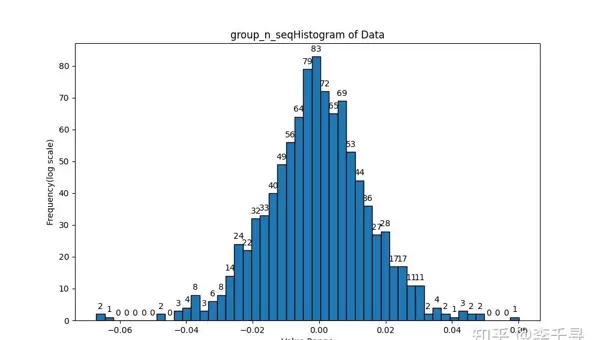
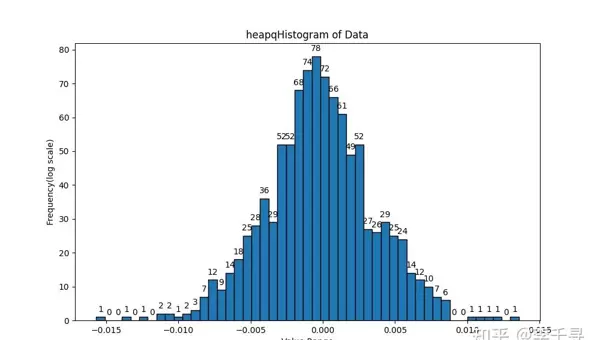
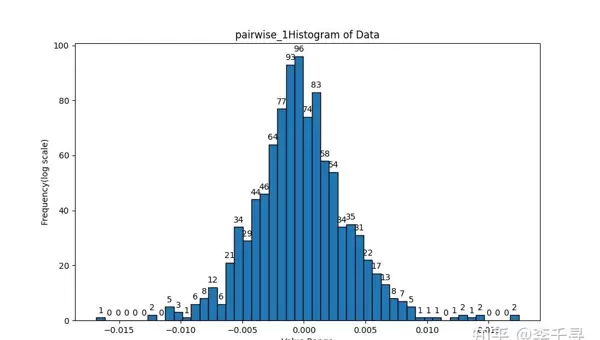
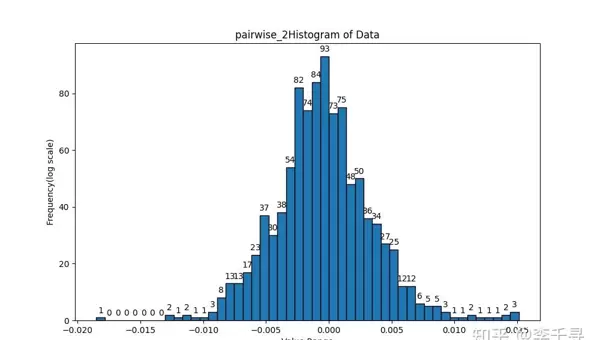
为验证累加顺序对最终结果的影响,可通过设计多种遍历路径的累加程序进行比对。以下为相关测试图像记录:
import numpy as np
import heapq
import matplotlib.pyplot as plt
import torch
from tqdm import tqdm
class CustomCompare:
def __init__(self, value):
self.value = np.float32(value)
def __lt__(self, other):
return abs(self.value) < abs(other.value)
def __repr__(self):
return str(self.value)
def __add__(self, other):
if isinstance(other, CustomCompare):
return CustomCompare(self.value + other.value)
# 卡汉求和
def kahan_sum(arr, chunk_size=128):
total_sum = np.float32(0.0)
total_c = np.float32(0.0)
total_g_sum = np.float32(0.0)
total_g_c = np.float32(0.0)
for i in range(0, len(arr), chunk_size):
chunk = arr[i:i+chunk_size]
chunk = np.pad(chunk, (0,chunk_size - chunk.size), mode='constant', constant_values=(0.0,))
y = chunk - total_g_c
t = total_g_sum + y
total_g_c = (t - total_g_sum) - y
total_g_sum = t
for x in total_g_sum:
y = x - total_c
t = total_sum + y
total_c = (t - total_sum) - y
total_sum = t
return total_sum
def build_min_heap(data):
heap = [CustomCompare(x) for x in data]
heapq.heapify(heap)
return heap
# 绝对值最小堆累加
def accumulate_min_heap(heap):
result = 0
max_process = 0
while len(heap) > 1:
min1 = heapq.heappop(heap)
min2 = heapq.heappop(heap)
current_sum = (min1 + min2)
result = current_sum
if abs(min1.value - min2.value) > max_process:
max_process = abs(min1.value - min2.value)
heapq.heappush(heap, current_sum)
return result.value, max_process
# 排序后顺序累加
def reduce_sort_array(arr):
arr.sort()
max_process = 0
res = arr[-1]
for i in range(len(arr)-1):
if abs(res - arr[i]) > max_process:
max_process = abs(res - arr[i])
res += arr[i]
return res, max_process
# 不排序直接顺序累加
def reduce_array(arr):
res = arr[0]
max_process = 0
for i in range(1,len(arr)):
if abs(res - arr[i]) > max_process:
max_process = abs(res - arr[i])
res += arr[i]
return res, max_process
# 折半累加 sub_arr[:len(sub_arr)//2] + sub_arr[len(sub_arr)//2:]
def pairwise_sum_1(arr):
max_value = np.float32('-inf')
def recursive_sum(sub_arr):
nonlocal max_value
if len(sub_arr) == 1:
return sub_arr[0], max_value
if len(sub_arr) % 2 == 1:
sub_arr = np.append(sub_arr, 0.0)
new_arr = sub_arr[:len(sub_arr)//2] + sub_arr[len(sub_arr)//2:]
max_value = max(max_value, np.max(np.abs(sub_arr[:len(sub_arr)//2] - sub_arr[len(sub_arr)//2:])))
return recursive_sum(new_arr.astype(np.float32))
return recursive_sum(arr.astype(np.float32))
# 间隔累加 sub_arr[::2] + sub_arr[1::2]
def pairwise_sum_2(arr):
max_value = np.float32('-inf')
def recursive_sum(sub_arr):
nonlocal max_value
if len(sub_arr) == 1:
return sub_arr[0], max_value
if len(sub_arr) % 2 == 1:
sub_arr = np.append(sub_arr, 0.0)
new_arr = sub_arr[::2] + sub_arr[1::2]
max_value = max(max_value, np.max(np.abs(sub_arr[::2] - sub_arr[1::2])))
return recursive_sum(new_arr.astype(np.float32))
return recursive_sum(arr.astype(np.float32))
# 分组累加,组间顺序累加,每组n个元素累加(默认每组10个元素)
def group_n_seq_sum(arr, group_num=10):
max_value = np.float32(0.0)
res = np.float32(0.0)
ele_num = arr.size
paddings_size = (group_num - (ele_num % group_num)) % group_num
padded_arr = np.pad(arr, (0, paddings_size), 'constant',constant_values=(0.0,))
for i in range(padded_arr.size // group_num):
res_group = np.float32(0.0)
for j in range(group_num):
res_group += padded_arr[i * group_num + j]
max_value = max(abs(res_group - padded_arr[i * group_num + j]), max_value)
res += res_group
max_value = max(abs(res - res_group), max_value)
return res, max_value
# 分组累加,组间二分累加,每组n个元素累加(默认每组10个元素)
def group_n_btree_sum(arr, group_num=10):
max_value = np.float32(0.0)
def recursive_sum(sub_arr):
nonlocal max_value
if len(sub_arr) == 1:
return sub_arr[0], max_value
if len(sub_arr) % 2 == 1:
sub_arr = np.append(sub_arr, 0.0)
new_arr = sub_arr[:len(sub_arr)//2] + sub_arr[len(sub_arr)//2:]
max_value = np.float32(max(max_value, np.max(np.abs(sub_arr[:len(sub_arr)//2] - sub_arr[len(sub_arr)//2:]))))
return recursive_sum(new_arr.astype(np.float32))
res = np.float32(0.0)
ele_num = arr.size
paddings_size = (group_num - (ele_num % group_num)) % group_num
padded_arr = np.pad(arr, (0, paddings_size), 'constant',constant_values=(0.0,))
for i in range(padded_arr.size // group_num):
res_group = np.float32(0.0)
for j in range(group_num):
res_group += padded_arr[i * group_num + j]
max_value = np.float32(max(abs(res_group - padded_arr[i * group_num + j]), max_value))
res = np.append(res, res_group)
return recursive_sum(res)
def plot_histogram(data, fig_name, num):
data_min = np.min(data)
data_max = np.max(data)
bins = np.linspace(data_min, data_max, num)
hist, edges = np.histogram(data, bins=bins)
plt.figure(figsize=(10,6))
plt.bar(edges[:-1], hist, width=np.diff(edges), edgecolor='black')
for i, v in enumerate(hist):
plt.text(edges[i], v+ 1, str(v),ha='center',va='bottom')
plt.title(fig_name+"Histogram of Data")
plt.xlabel("Value Range")
plt.ylabel("Frequency(log scale)")
plt.savefig('./prof/'+fig_name+'.png')
# plt.show()
plt.close()
# Generate random float32 data
# np.random.seed(20)
list_kahan = []
list_group_n_seq = []
list_group_n_btree = []
list_pairwise_1_diff = []
list_pairwise_2_diff = []
list_arrange_diff = []
list_arrange_sort_diff = []
list_heapq_diff = []
for i in tqdm(range(1000), desc="Processing"):
mean_1 = torch.FloatTensor(1).uniform_(-25, 25).item()
mean_2 = torch.FloatTensor(1).uniform_(-25, 25).item()
# print("均值:", mean_1)
# print("均值:", mean_2)
std_dev_1 = torch.FloatTensor(1).uniform_(1, 25).item()
std_dev_2 = torch.FloatTensor(1).uniform_(1, 25).item()
# print("标准差:", std_dev_1)
# print("标准差:", std_dev_2)
shape = (4000,)
float32_data = \
torch.normal(mean=torch.full(shape, mean_1), std=torch.full(shape, std_dev_1)).to(torch.float32).numpy() + \
torch.normal(mean=torch.full(shape, mean_2), std=torch.full(shape, std_dev_2)).to(torch.float32).numpy()
# 累加方式
kahan_result_float32 = kahan_sum(float32_data)
group_n_seq_result_float32, max_process_group_n_seq = group_n_seq_sum(float32_data, 32)
group_n_btree_result_float32, max_process_group_n_btree = group_n_btree_sum(float32_data, 32)
pairwise_result_float32_1, max_process_pairwise_1 = pairwise_sum_1(float32_data)
pairwise_result_float32_2, max_process_pairwise_2 = pairwise_sum_2(float32_data)
arrange_result_float32, max_process_arrange = reduce_array(float32_data)
arrange_sort_result_float32, max_process_arrange_sort = reduce_sort_array(float32_data)
heapq_result_float32, max_process_heapq = accumulate_min_heap(build_min_heap(float32_data))
# 标杆生成
# result_float64 = accumulate_min_heap(build_min_heap(float32_data.astype(np.float64)))
result_float64 = kahan_sum(float32_data.astype(np.float64))
# print("Result(卡汉求和) :", kahan_result_float32,"\tdiff:", result_float64 - kahan_result_float32)
# print("Result(分组累加+组间顺序) :", group_n_seq_result_float32, "\tmax_process:", max_process_group_n_seq,"\tdiff:", result_float64 - group_n_seq_result_float32)
# print("Result(分组累加+组间二叉树):", group_n_btree_result_float32, "\tmax_process:", max_process_group_n_btree,"\tdiff:", result_float64 - group_n_btree_result_float32)
# print("Result(折半累加) :", pairwise_result_float32_1, "\tmax_process:", max_process_pairwise_1,"\tdiff:", result_float64 - pairwise_result_float32_1)
# print("Result(间隔累加) :", pairwise_result_float32_2, "\tmax_process:", max_process_pairwise_2,"\tdiff:", result_float64 - pairwise_result_float32_2)
# print("Result(顺序累加) :", arrange_result_float32, "\tmax_process:", max_process_arrange,"\tdiff:", result_float64 - arrange_result_float32)
# print("Result(排序后顺序累加) :", arrange_sort_result_float32, "\tmax_process:", max_process_arrange_sort,"\tdiff:", result_float64 - arrange_sort_result_float32)
# print("Result(绝对值最小堆累加) :", heapq_result_float32, "\tmax_process:", max_process_heapq,"\tdiff:", result_float64 - heapq_result_float32)
# print("Result(fp64真值) :", result_float64)
list_kahan.append(result_float64 - kahan_result_float32)
list_group_n_seq.append(result_float64 - group_n_seq_result_float32)
list_group_n_btree.append(result_float64 - group_n_seq_result_float32)
list_pairwise_1_diff.append(result_float64 - pairwise_result_float32_1)
list_pairwise_2_diff.append(result_float64 - pairwise_result_float32_2)
list_arrange_diff.append(result_float64 - arrange_result_float32)
list_arrange_sort_diff.append(result_float64 - arrange_sort_result_float32)
list_heapq_diff.append(result_float64 - heapq_result_float32)
list_kahan = np.array(list_kahan)
list_group_n_seq = np.array(list_group_n_seq)
list_group_n_btree = np.array(list_group_n_btree)
list_pairwise_1_diff = np.array(list_pairwise_1_diff)
list_pairwise_2_diff = np.array(list_pairwise_2_diff)
list_arrange_diff = np.array(list_arrange_diff)
list_arrange_sort_diff = np.array(list_arrange_sort_diff)
list_heapq_diff = np.array(list_heapq_diff)
plot_histogram(list_kahan, "kahan", 50)
plot_histogram(list_group_n_seq, "group_n_seq", 50)
plot_histogram(list_group_n_btree, "group_n_btree", 50)
plot_histogram(list_pairwise_1_diff, "pairwise_1", 50)
plot_histogram(list_pairwise_2_diff, "pairwise_2", 50)
plot_histogram(list_arrange_diff, "arrange", 50)
plot_histogram(list_arrange_sort_diff, "arrange_sort", 50)
plot_histogram(list_heapq_diff, "heapq", 50)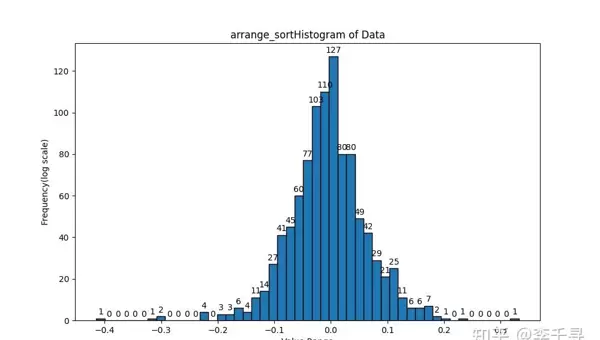




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







