在机器学习的预处理流程中,降维是一项至关重要的技术。其中,主成分分析(PCA)作为最经典和广泛使用的降维方法之一,不仅在实际项目中频繁应用,也是面试考察的重点内容。本文将从PCA的必要性出发,深入剖析其核心思想与数学原理,推导关键步骤,并结合Python代码进行实战演示,力求让初学者也能轻松理解并上手使用。
一、PCA的核心理念:以少胜多,保留关键信息
高维数据常面临诸多挑战:特征数量庞大导致计算效率低下、部分特征之间存在高度相关性(即多重共线性),以及难以直接可视化等问题。PCA的解决思路非常清晰:
- 在降低维度的同时,尽可能保留原始数据的信息
- 识别出数据中方差最大的方向——这些被称为“主成分”,能够最好地反映数据的分布结构
- 选取前k个最重要的主成分来替代原始的n个特征(满足k远小于n),实现有效的维度压缩
本质上,PCA是将原始数据从n维空间投影到一个k维的新空间(主成分空间),使得投影后的数据信息损失最小化。
举个生活化的例子:如果用“身高”和“体重”两个指标描述一个人的体型,这两个变量通常具有一定相关性。PCA可以构造一个新的综合指标——例如“体型指数”,它融合了身高与体重的主要变化趋势,从而用一个特征代替两个,完成降维任务。
二、PCA背后的数学逻辑:三大核心步骤
理解PCA并不需要精通所有公式推导,掌握以下三个关键环节即可:
-
数据标准化(必须执行)
由于不同特征可能具有不同的量纲(如身高单位为厘米,体重为千克),这会影响方差的计算结果。因此,需对所有特征进行标准化处理,使其均值为0、标准差为1,转化为标准正态分布形式。
标准化后的值 = (原始值 - 特征均值) / 特征标准差 -
构建协方差矩阵
协方差矩阵用于衡量各特征之间的线性关系:
- 对角线上的元素表示各个特征自身的方差,值越大说明该特征携带的信息越多
- 非对角线元素代表两个特征间的协方差:若为0则无相关性;正值表示正相关;负值表示负相关
-
特征值分解与主成分选择
对协方差矩阵进行特征值分解,得到:
- 特征值:反映对应主成分所解释的方差大小,值越大越重要
- 特征向量:指示主成分的方向,即数据投影的新轴方向
选择前k个最大特征值对应的特征向量组成投影矩阵,将原始数据乘以此矩阵,即可获得降维后的k维表示。
三、实战演练:基于sklearn实现PCA(鸢尾花数据集)
接下来我们使用经典的鸢尾花数据集进行实操演示,该数据集包含4个特征,目标是将其降至2维以便于可视化展示。
1. 环境配置
确保已安装以下依赖库:
pip install numpy pandas matplotlib scikit-learn
2. 完整代码实现(含详细注释)
# 1. 导入库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import matplotlib
matplotlib.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
matplotlib.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# 2. 加载数据
iris = load_iris()
X = iris.data # 原始数据:4个特征(花萼长、花萼宽、花瓣长、花瓣宽)
y = iris.target # 标签:3类鸢尾花
# 3. 数据标准化(关键步骤)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X) # 标准化后的数据
# 4. 初始化PCA模型,降维到2维
pca = PCA(n_components=2) # n_components:目标维度
X_pca = pca.fit_transform(X_scaled) # 执行PCA降维
# 5. 查看结果
print("原始数据维度:", X.shape) # 输出:(150, 4)
print("降维后数据维度:", X_pca.shape) # 输出:(150, 2)
# 查看各主成分的方差解释比例(重要!评估降维效果)
print("各主成分方差解释比例:", pca.explained_variance_ratio_)
print("累计方差解释比例:", sum(pca.explained_variance_ratio_)) # 通常保留80%以上
# 6. 可视化降维结果
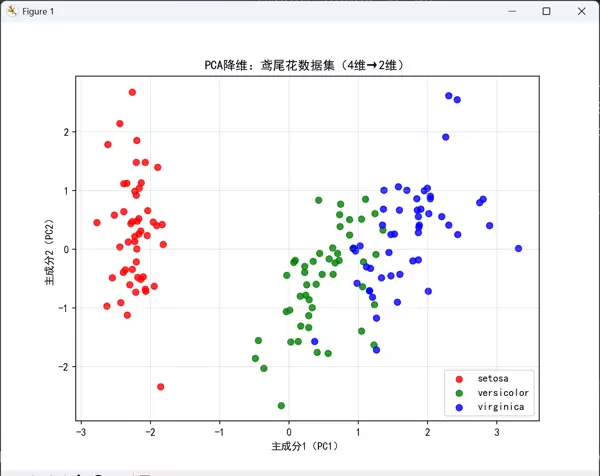
plt.figure(figsize=(8, 6))
colors = ['red', 'green', 'blue']
labels = iris.target_names
for i in range(3):
plt.scatter(X_pca[y == i, 0], X_pca[y == i, 1], c=colors[i], label=labels[i], alpha=0.8)
plt.xlabel('主成分1(PC1)')
plt.ylabel('主成分2(PC2)')
plt.title('PCA降维:鸢尾花数据集(4维→2维)')
plt.legend()
plt.grid(alpha=0.3)
plt.show()3. 过程解析与结果说明
本段代码实现了对鸢尾花数据集的PCA降维与可视化输出,具体流程如下:
- 导入必要的工具包,包括numpy(数值运算)、pandas(数据处理)、matplotlib(绘图)及scikit-learn中的相关模块
- 加载数据集,共150条样本,每条包含4个连续型特征(花萼长度、宽度,花瓣长度、宽度)和类别标签
- 采用StandardScaler对数据进行标准化处理,消除因量纲差异带来的影响
- 初始化PCA模型,设定目标维度为2,执行降维操作
- 输出结果显示,数据形状由(150, 4)变为(150, 2),成功压缩维度
- 打印各主成分的方差解释比例,用于评估信息保留程度
- 通过二维散点图进行可视化,不同颜色代表三类鸢尾花品种,横纵坐标分别为第一和第二主成分
最终图像显示,在仅保留两个主成分的情况下,三类样本仍能形成较为清晰的聚类边界,表明PCA有效保留了原始数据的关键分类信息。
4. 结果解读
降维后数据维度由4维降至2维,累计方差解释率达到约97%,意味着原始数据中超过九成的信息被保留下来。
从可视化图可见,三类鸢尾花在二维空间中分离明显,说明即使经过大幅降维,类别间的判别特征依然得以维持。
四、如何确定最优主成分个数k?两种实用策略
选择合适的k值是PCA应用中的关键决策,目的在于平衡“压缩程度”与“信息保留”。推荐以下两种常用方法:
-
方差解释比例法(最常用)
设定一个阈值(如0.95),要求累计解释方差比例不低于该值,PCA会自动选择满足条件的最小k值。
运行如下代码可生成一张图表,展示累计方差随主成分数量增加的变化趋势:n_components# 1. 导入库 import numpy as np import pandas as pd import matplotlib.pyplot as plt from sklearn.datasets import load_iris from sklearn.preprocessing import StandardScaler from sklearn.decomposition import PCA import matplotlib matplotlib.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签 matplotlib.rcParams['axes.unicode_minus'] = False # 用来正常显示负号 # 2. 加载数据 iris = load_iris() X = iris.data # 原始数据:4个特征(花萼长、花萼宽、花瓣长、花瓣宽) y = iris.target # 标签:3类鸢尾花 # 3. 数据标准化(关键步骤) scaler = StandardScaler() X_scaled = scaler.fit_transform(X) # 标准化后的数据 # 4. 使用方差解释比例法自动选择k值,并可视化累计方差解释比例 # 计算所有主成分的方差解释比例 pca_full = PCA() # 不指定k值,计算所有可能的主成分 pca_full.fit(X_scaled) # 计算累计方差解释比例 cumulative_variance = np.cumsum(pca_full.explained_variance_ratio_) # 绘制累计方差解释比例图 plt.figure(figsize=(10, 6)) plt.plot(range(1, len(cumulative_variance) + 1), cumulative_variance, 'bo-', linewidth=2, markersize=8) plt.axhline(y=0.95, color='r', linestyle='--', alpha=0.7, label='95% 方差阈值') plt.axvline(x=np.argmax(cumulative_variance >= 0.95) + 1, color='g', linestyle='--', alpha=0.7, label='最佳k值') # 标记95%阈值对应的点 k_95 = np.argmax(cumulative_variance >= 0.95) + 1 plt.scatter(k_95, cumulative_variance[k_95-1], s=200, c='red', zorder=5, label=f'k={k_95} (95%方差)') plt.xlabel('主成分数量 (k)', fontsize=12) plt.ylabel('累计方差解释比例', fontsize=12) plt.title('累计方差解释比例 vs 主成分数量', fontsize=14) plt.grid(True, alpha=0.3) plt.legend() plt.xticks(range(1, len(cumulative_variance) + 1)) # 在图中添加文本信息 plt.text(len(cumulative_variance), 0.5, f'自动选择 k={k_95}\n保留方差:{cumulative_variance[k_95-1]:.3f}', bbox=dict(boxstyle="round,pad=0.3", facecolor="yellow", alpha=0.7)) plt.tight_layout() plt.show() # 使用95%阈值自动选择k值 pca_auto = PCA(n_components=0.95) X_pca_auto = pca_auto.fit_transform(X_scaled) print(f"自动选择的k值:{pca_auto.n_components_}") print(f"累计方差解释比例:{sum(pca_auto.explained_variance_ratio_):.4f}")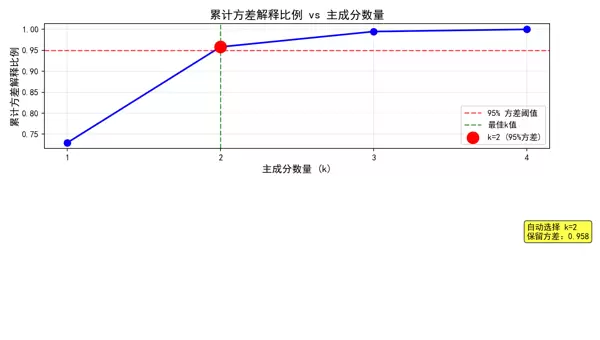
-
特征值碎石图法(Scree Plot)
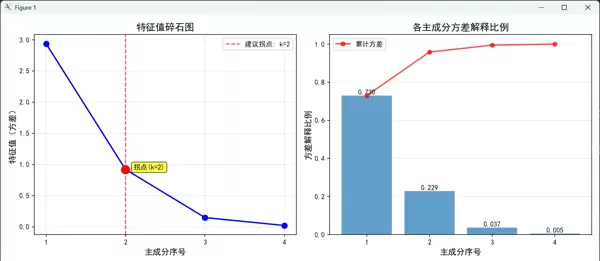
绘制每个主成分对应的特征值曲线,寻找“拐点”位置——即曲线由陡峭转为平缓之处,此后新增主成分带来的信息增益较小,可作为截断点。
# 1. 导入库 import numpy as np import pandas as pd import matplotlib.pyplot as plt from sklearn.datasets import load_iris from sklearn.preprocessing import StandardScaler from sklearn.decomposition import PCA import matplotlib matplotlib.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签 matplotlib.rcParams['axes.unicode_minus'] = False # 用来正常显示负号 # 2. 加载数据 iris = load_iris() X = iris.data # 原始数据:4个特征(花萼长、花萼宽、花瓣长、花瓣宽) y = iris.target # 标签:3类鸢尾花 # 3. 数据标准化(关键步骤) scaler = StandardScaler() X_scaled = scaler.fit_transform(X) # 标准化后的数据 # 4. 特征值碎石图法 - 绘制特征值随主成分个数的变化曲线 pca_full = PCA() # 不指定k,计算所有主成分 pca_full.fit(X_scaled) # 获取特征值(方差大小) eigenvalues = pca_full.explained_variance_ # 创建图形 plt.figure(figsize=(12, 5)) # 子图1:特征值碎石图 plt.subplot(1, 2, 1) plt.plot(range(1, len(eigenvalues) + 1), eigenvalues, 'bo-', linewidth=2, markersize=8) plt.xlabel('主成分序号', fontsize=12) plt.ylabel('特征值(方差)', fontsize=12) plt.title('特征值碎石图', fontsize=14) plt.grid(True, alpha=0.3) plt.xticks(range(1, len(eigenvalues) + 1)) # 计算二阶差分找到"拐点"(特征值变化最平缓的点) if len(eigenvalues) > 2: # 计算特征值的变化率(一阶差分) first_diff = np.diff(eigenvalues) # 计算变化率的变化(二阶差分)来找到拐点 second_diff = np.diff(first_diff) # 找到二阶差分最大(变化最平缓)的点作为拐点建议 if len(second_diff) > 0: inflection_point = np.argmax(second_diff) + 2 # +2 因为二阶差分比原序列短2个元素 plt.axvline(x=inflection_point, color='r', linestyle='--', alpha=0.7, label=f'建议拐点: k={inflection_point}') # 标记拐点 plt.scatter(inflection_point, eigenvalues[inflection_point - 1], s=150, c='red', zorder=5) # 添加拐点说明 plt.text(inflection_point + 0.1, eigenvalues[inflection_point - 1], f'拐点(k={inflection_point})', fontsize=10, bbox=dict(boxstyle="round,pad=0.3", facecolor="yellow", alpha=0.7)) plt.legend() # 子图2:特征值贡献率(方差解释比例)条形图 plt.subplot(1, 2, 2) explained_ratio = pca_full.explained_variance_ratio_ bars = plt.bar(range(1, len(explained_ratio) + 1), explained_ratio, alpha=0.7) plt.xlabel('主成分序号', fontsize=12) plt.ylabel('方差解释比例', fontsize=12) plt.title('各主成分方差解释比例', fontsize=14) plt.grid(True, alpha=0.3, axis='y') plt.xticks(range(1, len(explained_ratio) + 1)) # 在柱状图上添加数值标签 for i, (bar, ratio) in enumerate(zip(bars, explained_ratio)): height = bar.get_height() plt.text(bar.get_x() + bar.get_width() / 2., height, f'{ratio:.3f}', ha='center', va='bottom', fontsize=10) # 添加累计方差线 cumulative_ratio = np.cumsum(explained_ratio) plt.plot(range(1, len(cumulative_ratio) + 1), cumulative_ratio, 'ro-', markersize=6, linewidth=2, alpha=0.7, label='累计方差') plt.legend() plt.tight_layout() plt.show() # 5. 输出关键信息 print("=" * 50) print("特征值碎石图分析结果:") print("=" * 50) print(f"所有特征值: {eigenvalues}") print(f"特征值解释比例: {explained_ratio}") print(f"累计解释比例: {cumulative_ratio}") # 基于"拐点法则"建议的k值 if len(eigenvalues) > 2: print(f"\n基于碎石图拐点法则建议的k值: {inflection_point}") print(f"前{inflection_point}个主成分的累计方差解释比例: {cumulative_ratio[inflection_point - 1]:.4f}") # 对比"肘部法则"(特征值 > 1 的标准) k_elbow = sum(eigenvalues > 1) print(f"基于特征值>1的肘部法则建议的k值: {k_elbow}") print(f"前{k_elbow}个主成分的累计方差解释比例: {cumulative_ratio[k_elbow - 1]:.4f}") # 6. 使用建议的k值进行PCA降维 print("\n" + "=" * 50) print("使用建议k值进行PCA降维:") print("=" * 50) if len(eigenvalues) > 2: # 使用拐点建议的k值 k_suggested = inflection_point pca_suggested = PCA(n_components=k_suggested) X_pca_suggested = pca_suggested.fit_transform(X_scaled) print(f"使用k={k_suggested}降维后维度: {X_pca_suggested.shape}") print(f"累计方差解释比例: {sum(pca_suggested.explained_variance_ratio_):.4f}") else: print("数据维度太少,无法计算拐点")此代码将输出一个双子图布局:
- 左图(特征值碎石图):显示各主成分的特征值大小,红色虚线标记建议的拐点位置,利用二阶差分法自动检测变化最缓慢的节点
- 右图(方差解释比例图):柱状图展示每个主成分独立解释的方差比例,红色折线表示累计比例,并在柱顶标注具体数值
五、PCA的应用场景与局限性分析
尽管PCA功能强大,但其适用范围有一定边界,了解其优势与限制有助于更合理地使用该方法。
一、应用场景
在面对高维数据时,例如图像处理或文本分类中存在大量特征的场景,PCA 能有效降低数据维度,提升计算效率。此外,它也广泛应用于数据可视化领域,通过将高维数据投影到二维或三维空间,便于直观观察数据的整体分布结构。
在数据去噪方面,PCA 同样表现出色。其通过保留方差较大的主成分,舍弃方差较小的成分,从而过滤掉可能代表噪声的信息,实现对原始数据的净化与重构。
二、局限性分析
尽管 PCA 具备诸多优势,但也存在一定限制。首先,它对异常值较为敏感,因为异常点会显著影响协方差矩阵和方差的计算结果,因此在应用前通常需要对数据进行清洗或标准化处理。
其次,PCA 属于线性降维方法,只能捕捉变量之间的线性关系,难以应对具有复杂非线性结构的数据分布。在这种情况下,可考虑使用如 LDA 或 t-SNE 等更适合处理非线性模式的算法。
另外,主成分本身往往缺乏明确的业务解释性。由于每个主成分是原始特征的线性组合,其数值难以直接对应实际意义,这在某些需要强可解释性的应用场景中可能构成障碍。
三、总结与实践建议
PCA 是机器学习中最为基础且实用的降维工具之一,其核心思想在于“通过最大化方差来保留数据中的关键信息”。深入理解其数学原理并结合实际操作,有助于高效应对高维数据带来的挑战。
本文提供的代码示例可直接复制运行,推荐尝试替换不同数据集(如 MNIST 手写数字数据集或波士顿房价数据集),以体验 PCA 在多种任务中的表现差异。




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







