发帖
雷达卡
本帖隐藏的内容
K-MeansIt is a type of unsupervised algorithm which solves the clustering problem. Its procedure follows a simple and easy way to classify a given data set through a certain number of clusters (assume k clusters). Data points inside a cluster are homogeneous and heterogeneous to peer groups.
Remember figuring out shapes from ink blots? k means is somewhat similar this activity. You look at the shape and spread to decipher how many different clusters / population are present!
How K-means forms cluster:
- K-means picks k number of points for each cluster known as centroids.
- Each data point forms a cluster with the closest centroids i.e. k clusters.
- Finds the centroid of each cluster based on existing cluster members. Here we have new centroids.
- As we have new centroids, repeat step 2 and 3. Find the closest distance for each data point from new centroids and get associated with new k-clusters. Repeat this process until convergence occurs i.e. centroids does not change.
How to determine value of K:
In K-means, we have clusters and each cluster has its own centroid. Sum of square of difference between centroid and the data points within a cluster constitutes within sum of square value for that cluster. Also, when the sum of square values for all the clusters are added, it becomes total within sum of square value for the cluster solution.
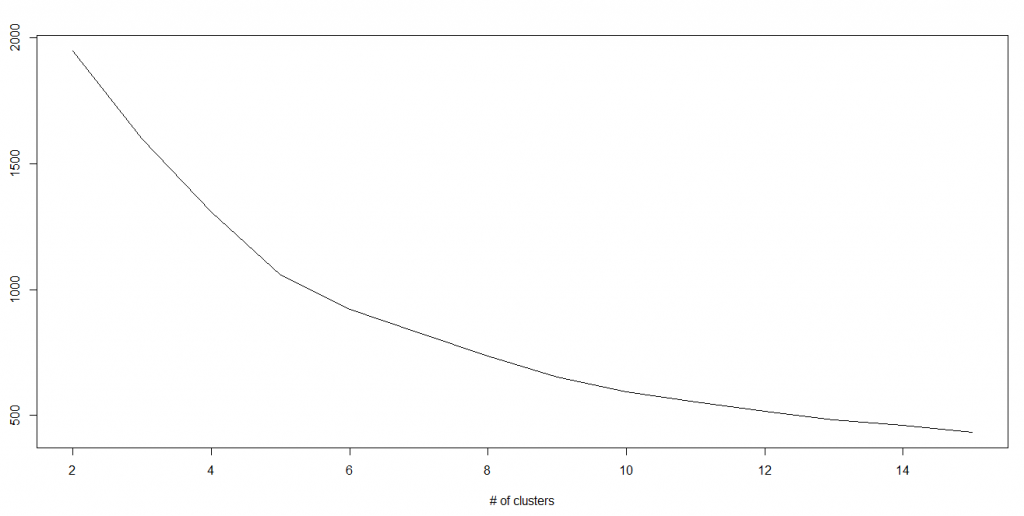
We know that as the number of cluster increases, this value keeps on decreasing but if you plot the result you may see that the sum of squared distance decreases sharply up to some value of k, and then much more slowly after that. Here, we can find the optimum number of cluster.
- #Import Library
- from sklearn.cluster import KMeans
- #Assumed you have, X (attributes) for training data set and x_test(attributes) of test_dataset
- # Create KNeighbors classifier object model
- k_means = KMeans(n_clusters=3, random_state=0)
- # Train the model using the training sets and check score
- model.fit(X)
- #Predict Output
- predicted= model.predict(x_test)
R Code
- library(cluster)
- fit <- kmeans(X, 3) # 5 cluster solution
京公网安备 11010802022788号
