发帖
雷达卡
导言：说话沟通，是最基本而广泛的人类活动之一。比如病人向医生诉说病情，医生向病人交代医嘱；商人通过磋商达成共识；商家设计广告词影响消费者；求职者之间交流岗位信息；政治家通过演讲影响选举结果；政府通过cctv影响舆论；当然还有恋人夫妻之间说话聊天交流感情。关于说话沟通一个基本问题是：人类在有利可图时是否一定会说谎？人类说谎有什么规律？
一、说谎的基本特征
在上一期《说谎的行为经济学（1）》我们介绍了一个简单的掷骰子报告实验（Fischbacher & Föllmi-Heusi 2013）：一群参与者，每人掷一颗六面的骰子。每人看到自己的点数后报告给实验人员，实验人员根据点数来给钱：6点不给钱，1点给10元，2点给20元，3点给30元，4点给40元，5点给50元。注意，在这个情景里，无论自己真实掷出的点数为多少，谎报给实验人员自己掷到了5点总是有利可图的。因此这是一个测试说谎的实验。
下面的图1展示了众多来自经济学、心理学、社会学的对骰子报告重复（和变型）实验的结果（摘自Abeler, Nosenzo & Raymond, forthcoming）。如果所有人都如实报告，按照概率，每个点数出现的概率都应该为1/6，即图中虚线的位置。如果报告某个点数的比例显著偏离该位置，就说明有人说谎了。图中的加粗黑线标示了众多实验的平均值。
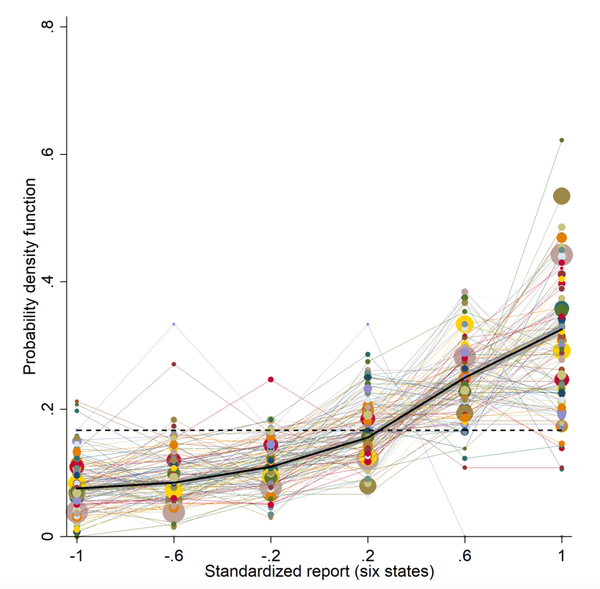
图1：多个骰子报告实验的结果。
横轴为根据收益排序的报告点数：-1对应6点（收益最低），-.6对应1点，……，.6对应4点，1对应5点（收益最高）。纵轴为频率。每一条折线连结连结起来的点对应一个实验组的数据。摘自：Abeler, Nosenzo & Raymond, Econometrica forthcoming.
基于这个测试说谎的骰子报告实验的结果，我们可以总结出一些说谎的基本特征：
第一，平均而言，人们的说谎程度要远低于所有人都是说最大的谎以赚最多钱的程度。注意到，如果所有人都只图利益，那应该所有人都报告掷到了5点，因此报告5点的比例应接近百分之一百。然而，从图1中可以看到，报告5点的比例大约只有百分之三十，远低于百分之一百。同时，如果我们相信没有人会掷出了其他点数却去报告6点，那么所有报告6点的人都可以认为是完全诚实的人。从图中可以看到，报告6点的人的比例大概是潜在概率1/6的一半。所以我们可以认为完全诚实的人大约占到整个人口的二分之一。简而言之，我们所处的社会是一个多样性的社会——有很多说谎的人，也有很多不说谎或不说最大程度的谎的人。
第二，人们的确不是一说谎就会说最大的谎。除了报告收益最高的5点的比例高过1/6，报告收益为次高的4点的比例也高过了1/6。这很有意思，说明并不是一个人一说谎就会说最大的谎（报5点），而是说谎的心理成本随说谎程度的增加而增加，表明人们决策时会在说多大程度的谎和金钱收益之间作出权衡。
第三，图中的加粗黑线标示了多个实验的平均值，可以看到，报告某点数的比例随该点数收益的增加而严格递增。
下面，我们介绍一个能同时解释以上三个特征的简单模型。在明白了这个基本模型之后，我们会再讨论有没有别的社会或心理因素也在起作用。
从骰子报告实验的结果可以看出：（1）说谎有成本，并且与说谎的程度相关；（2）不同人的说谎成本可能不同。我们的模型解释要包含这两点。
我们可以假设：说谎的效用 = 说谎的收益 - 说谎的心理成本；并且，说谎的心理成本随说谎程度的增加而增加。具体地，设掷出骰子的真实点数为 
。用 
来表示一个参与者的报告。为方便起见，假设金钱收益等于报告的点数 
，即 越大钱越多。我们用参数 
表示该参与者对说谎的”厌恶程度“——不同的参与者可能有不同的 
。
我们假设每个参与者选择报告 去最大化以下效用函数：
上式右边的第一项为报告的点数，代表了金钱收益。第二项为说谎所产生的心理成本。 
表示成本随报告与真实点数之间的偏离程度的增加而增加。同时， 越大表示说谎越有心理负担。
基于这个效用函数，我们可以求得，根据每个参与者的真实点数 
和心理成本参数 
，他的最优报告点数是
我们可以称上式为说谎的基本公式。该公式体现出模型的三个特点：
第一，报告 总是大于等于真实点数 ，即没有人有向下报告（y<x）的动机。这是因为向下报告既赚少了钱又要承担说谎的心理成本，所以不可能是最优的。
第二，谎言的程度 
完全由说谎的厌恶参数 决定，会随 的变大而变小。当 很大时，人们会倾向于说实话。
第三，由这个模型所导出的说谎行为完全是一个个人决策的问题。说不说谎，说多大的谎，完全与其他人的说谎行为无关。——这一点在以后我们谈到如何区分这个基本模型的解释和其他关于说谎行为的解释时会很关键。
现在我们来看看上面的说谎模型如何解释我们在骰子报告实验里观察到的说谎行为的三个基本特征：（1）有很多人会说谎，也有很多人不说谎；（2）人们不一定一说谎就说最大的谎；（3）不同谎言出现的概率——即报告某个点数的人的比率——会随该谎言带来的金钱收益的增加而增加。
第一点和第二点可以说是我们直接假设进模型里的：因为每个人可能有不同的 ，当然有可能有些人说大谎，有些人说小谎，有些人不说谎。
关于第三点，这个结果虽然听起来很直观，但其实不容易看出怎么从上面的模型中推出来。读者可能会想，既然人们会在金钱收益和说谎的心理成本之间做出权衡，那么更多人说收益更大的谎不是很正常么？但是注意到，说收益更大的谎（报告更大的 ）也意味着谎言的程度 也更大，也即心理成本也更大。因此这个权衡并不能直接推出一个谎言的金钱收益越大就会有越多人说。
另外，像一位朋友在上一期的评论区中提到的，当看到图1中报告不同点数的比例随收益递增时，可能一个更直观的猜想是，人们掷到点数越差时就越倾向于说谎。比如，与掷到4点的人相比，掷到1点的人更倾向于说谎。然而，在我们介绍的模型中，说谎的程度 是完全独立于本身掷到多少点的。
上面的模型解释说谎的第三个特征的逻辑如下，说出来之后也很简单：
首先考虑会报告1点的人。由于没有人会高报，因此会报告1点的人就只有那些掷出的点数是1点或0点的人（为方便说明我们把6替换为0了）。同时，他们对谎言的厌恶程度还必须足够大（ 足够大），否则，他们就会报告比1高的点以赚取更高收益。而报告2点的人会包括掷出点数为0、1、2的人，同时，他们对谎言的厌恶程度 也必须足够大，否则他们会报告更高的点数。但是这时候对 的要求就要比报告1点的情况宽松一点，因为就算有 稍小的人，如果他掷出的是0，他也可能会报告2，但他在任何情况下都不会报告1。因此，总体上看，报告2点的人肯定比报告1点的人多。……如此类推，越大的点数，总体上看报告的人就越多。
总结一下：为什么越大的点数越多人说？不是因为越大的点数本身有更大的金钱收益而吸引了更多人去说，而是因为小的点数只有那些足够诚实的人才会说，而大的点数既会有那些不在乎说谎的人去说，又会有那些足够诚实的人去说（因为他们本身就掷到了相近的点数）。因此我们有——越夸张的谎言越多人说。
Reference
Abeler, J., Nosenzo, D., & Raymond, C. Preferences for truth-telling. Econometrica, forthcoming.
Xueheng Li：说谎的行为经济学（1）来源：知乎 www.zhihu.com
作者：Xueheng Li
，谢谢分享
京公网安备 11010802022788号
