minitab
已认证的官方帐号
在回归分析中,您希望回归模型有显著变量,并且产生一个高的R2值。小的P值/高的R2的组合表明预测量的变化和因变量的变化有关,并且您的模型解释了一些反应变异性。
这种组合似乎在一起很自然。但是如果您的回归模型有显著变量但是几乎不能说明变异性怎么办?这时候它有较小的P值和较低的R2。
乍一看,这个组合毫无意义。显著性预测是否仍有意义?让我们看下面这个例子!
高低R2值回归模型比较
这很难单独用数字来理解这种情况。调查显示为了正确理解回归分析结果,图像是必不可少的。当您可以看见到底发生了什么时,理解就变得容易了。
考虑到这一点,我将使用拟合线图。但是,一个二维的拟合线图只能显示有一个自变量和因变量的简单回归的结果。这个概念试用于多元线性回归,但是我不能绘制所需的更高维度的图形。
这些拟合线图显示了两个有几乎相同的回归方程的回归模型,但是上面的回归模型有个低的R2值,而另一个有较高的R2值。为了便于比较,我用相同比例来显示图形。这里是这两个例子的数据。


回归模型之间的相似点
这两个模型在一些方面几乎是一样的:
- 回归方程:y=44+2*x
- 两个模型输入都是显著的,P<0.001.
您可以看见两条回归线的向上斜率都是几乎为2,并且他们准确的依着目前数据集中显示的趋势。
P值的解释和输出的斜率对于输入变量并没改变。如果你通过增加一个单位自变量而在任一条线上右移,响应变量就会增加两个单位。对于两个模型来说,显著性P值说明你可以拒绝零假设,零假设是系数等于0(没显著效应)。
另外,如果你两个等式输入同样的预测变量,你可以通过计算发现输出变量几乎是相同的。举例来说,自变量输入10,输出为66.2,另个模型为64.8的预测输出。
回归模型中的不同
我打赌你在拟合线中注意到的第一件事就是:围绕着两个回归线数据的变化是截然不同的。R2和S(回归的标准差)在数值上描述了这种变化。
低的R2图像显示:即使杂乱的,变异较大的数据也可以有一个显著性趋势。趋势表明了即使数据点落在远离回归线的位置,自变量扔提供了关于因变量的信息。当你试图认为较低的R2值何变量是显著的是一致时,保持这个图像在脑海中!
像我们看见的,两个回归方程输出几乎相同的预测结果。但是,不同水平的变异度影响了这些预测的精度。
为了评估精度,我们来看看预测区间。预测区间是模型中给定具体自变量而得到的新的因变量的观察值可能的范围。区间越窄意味着预测更精准。下面是输入值为10时的拟合值和预测区间。
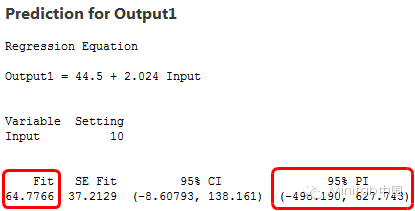
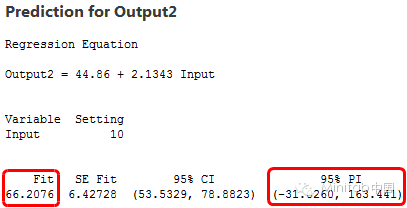
变异型大的模型产生了约从-500延伸到630的区间,超过1100个单位的预测区间!同时,变异型低的数据的模型产生了从-30到160的约200个单位的预测区间。很明显,有高的R2的模型预测更精确,即使拟合值是几乎一样的!
在看见实际数据中变量的分布后,精确度的不同应该是有意义的。当数据点进一步离散时,预测必须增加不确定性的反映。
结束语
让我们回顾一下我们所学到的:
- 系数估计趋势,R2代表围绕回归线的分布
- 不论模型R2值高低,对显著变量的理解都是一样的。
- 当你需要精确的预测值时,低的R2值是有问题的。
所以,如果你有显著性预测因子了但是你有一个低的R2值,那怎么办呢?我能听到你们中一些在说:“在模型中增加更多变量”。
在某些情况下,有可能增加更多的预测变量会提高模型的解释功效。但是,在其它情况下,数据包可能含有一个固有的更多的无法解释的变量。例如,因为人是无法预测的,许多心理研究中的R2就小于50%。

编辑于 2018-08-28




 雷达卡
雷达卡





 京公网安备 11010802022788号
京公网安备 11010802022788号







