发帖
雷达卡
Discussion of linear simultaneous equations systems may be found in almost all econometric textbooks. For example, Chapter 18 in Estimation and Inference in Econometrics by Russell Davidson and James G. MacKinnon (ISBN 0-19506011-3, Oxford University Press, 1993)
Linear Simultaneous Equations
|| Unconstrained Klein's Model I Example || Constrained Klein's Model I Example ||
Discussion of linear simultaneous equations systems may be found in almost all econometric textbooks. For example, Chapter 18 in Estimation and Inference in Econometrics by Russell Davidson and James G. MacKinnon (ISBN 0-19506011-3, Oxford University Press, 1993), or chapter 19 in Econometric Analysis, 2nd Ed. by William H. Greene (ISBN 0-02-346391-0, Macmillan, 1993).
The linear simultaneous equation model can be represented by the matrix equation:
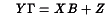
where Y is an TxK matrix of T observations on K endogenous variables, X is an TxL matrix of T observations on L exogenous variables, and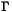 
is a KxK matrix of the coefficients among the endogenous variables, B is an LxK matrix of the coefficients of the endogenous variables on the exogenous, and Z is a TxK matrix of unobserved residuals.
Estimates for B and 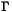are found by minimizing the log-likelihood:
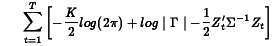
where
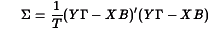
Not all of the elements of B and 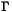can be estimated. To "identify" the model it is necessary to fix some elements of B and 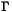to zero. It is also possible to fix elements of the residual covariance matrix to zero as well. The diagonal of 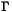is also fixed to one as a "normalization". See the references above for details about the identification of simultaneous models.
Klein's Model I is a well-known example that is presented in many econometrics textbooks, including the references above. From page 595, Greene (op.cit.) the equations for this model are: where C is consumption, I investment, Wp private wages, X equilibrium demand, P private profits, K capital stock, and where G is government spending, T is indirect business taxes plus net exports, Wg is the government wage bill, A is time trend measured from 1931. For this model, we get and and because the last three equations in the model are identities, the last three columns and rows in the residuals covariance matrix are fixed to zeros. The program for estimating the coefficients in this model, klein.prg,is written in the GAUSS programming language and uses Aptech System's Maximum Likelihood (MAXLIK) applications module. Estimates are produced for a 22 year time series of 9 variables of the U.S. economy from 1920 through 1941. The results are presented in klein.out Klein's Model I is a dynamic model because it contains autoregression coefficients, i.e., coefficients of endogenous variables on their values at a previous point in time. For such a model to be dynamically "stable" or stationary, the model estimates must satisfy a certain condition. Let For our estimates of Klein's Model I, we have and the absolute values of the eigenvalues of which are This confirms the stability of the model implied by our estimates. ||Top||HomePage|| Greene's book (op.cit.) contains an additional 32 years of data for Klein's Model I. Estimating the model with this additional data presents some difficulties that require the special features of Aptech System's Constrained Maximum Likelihood (CML) applications module. First, the data are highly correlated, causing difficulty for the estimation process, and second, the unconstrained estimation produces estimates that imply an unstable system. To deal with the first problem, CML is used to bound the coefficient estimates. For bounds we will use the 99% confidence limits from the analysis of the 1931 to 1942 data. For the second problem we will use CML to constrain the eigenvalues of The program for estimating the coefficients in this model, cklein.prg,is written in the GAUSS programming language and uses Aptech System's Constrained Maximum Likelihood (CML) applications module. Estimates are produced for the original 22 year time series of 9 variables of the U.S. economy from 1920 through 1941 plus in addition, the 32 year time series. The results are presented in klein.out The results of our stability test are: The Lagrangean coefficients associated with the constraints on these eigenvalues are: indicating that the model estimates are on the stability boundary.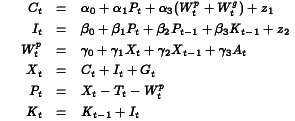
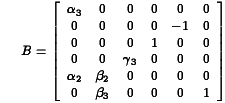
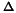be the submatrix of B associated with the relationships of the endogenous variables to the exogenous variables that are their lagged versions. Then stability requires that the eigenvalues of 
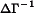be less than one in absolute value.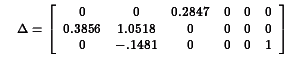 
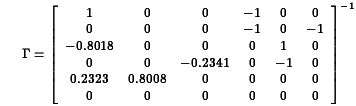
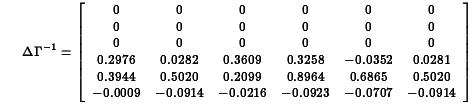
0.0000 0.0000 0.0000 0.0420 0.4911 0.4911
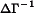to be less than one in absolute value. 0.0000 0.0000 0.0000 0.0026 0.9627 0.9627
0.0000 0.0000 0.0000 1.9556 0.0000 0.0000
[em09]
京公网安备 11010802022788号
