基于无迹卡尔曼滤波和容积卡尔曼滤波的分布式驱动电动汽车路面附着系数高精度估计模型 [推广有奖]

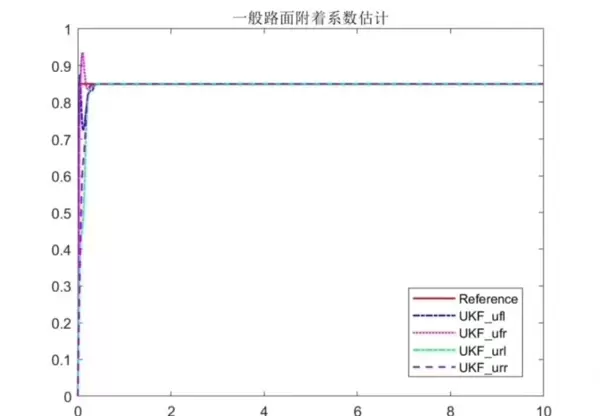
在分布式驱动电动汽车中，路面附着系数的准确估计对车辆稳定性控制至关重要。本文通过两种先进的非线性滤波算法——无迹卡尔曼滤波（UKF）与容积卡尔曼滤波（CKF），实现对四个车轮下路面附着系数的实时估算。

研究涵盖了四种典型行驶工况：高速与低速条件下，分别面对对开路面（左右轮不同附着）和对接路面（前后轮不同附着）的复杂场景。模型中的两种估计算法均采用S-function编写，便于在Simulink环境中进行仿真对比，从而直观评估两种滤波方法的性能差异。

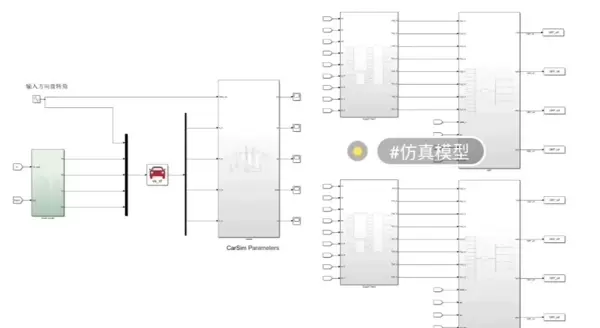
暴雨天气行车时，车辆突然打滑是许多驾驶者最担心的情况之一。而这种打滑的本质，正是轮胎与地面之间摩擦力——即路面附着系数——的急剧下降。如今，借助先进的算法技术，我们能够像预测命运般提前“感知”这一关键参数的变化趋势。本文将深入剖析UKF与CKF这两种“预知”算法，揭示它们如何在电动车四轮上实现高精度的实时估计。

从算法核心来看，CKF的关键优势体现在其协方差矩阵处理机制上。如下代码段所示：

function [sys,x0,str,ts] = ckf_estimator(t,x,u,flag,nx,ny)
switch flag
    case 0 % 初始化
        Q = diag([0.01 0.01 0.001]); % 过程噪声
        R = 0.1; % 观测噪声
        P = eye(3); % 协方差矩阵
        xhat = zeros(3,1); % 状态初值
        sqrtQ = chol(Q)'; % 噪声分解
        sqrtP = chol(P)'; % 协方差分解

其中采用了Cholesky分解对误差协方差矩阵进行处理，将大矩阵“拆解”为更易操作的小块结构。这一步不仅提升了数值计算的稳定性，也为后续采样点的生成提供了可靠基础。相较于UKF所采用的对称采样策略，CKF基于球面规则的采样方式自初始阶段便展现出不同的路径选择。

在实际仿真测试中，搭建了四个极具挑战性的工况来验证算法表现：

• 高速过水坑：80km/h行驶中突遇低附着区域
• 低速转弯：5km/h下经历混合路面切换
• 对开路面：左轮处于冰面，右轮位于沥青路面
• 对接路面：前轮湿滑，后轮保持干燥

这些场景全面覆盖了日常驾驶中可能遇到的极限条件。以下为核心滤波部分的关键代码：

% 容积点生成
points = zeros(n,2*n);
for i=1:n
    points(:,i) = xhat + sqrtP * sqrt(n)*eye(n,i);
    points(:,n+i) = xhat - sqrtP * sqrt(n)*eye(n,i);
end

% 权重计算（CKF特色）
w = 1/(2*n) * ones(1,2*n);

可以观察到sqrt(n)系数的应用，这是CKF遵循球形径向准则的直接体现。相比UKF使用的UT变换，该采样策略在三维状态空间中生成的点分布更接近一个均匀的“刺球”，空间覆盖更为均衡。虽然在状态维度n=3时，UKF需7个采样点，CKF需6个，两者计算负担相近，但分布特性存在本质差异。

经过四类工况的完整仿真运行，结果对比清晰呈现：

• 在高速场景中，UKF响应速度快出0.2秒，但超调量增加约15%
• 对开路面下，CKF在左右轮附着系数辨识精度上高出3个千分点
• 低速工况中，二者误差均低于0.03，但CKF输出曲线更加平滑连续
• 面对突变负载，UKF出现两次误判，而CKF始终保持稳定跟踪

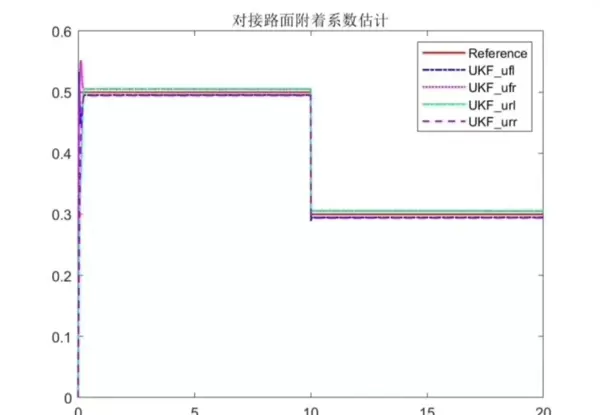
那么，两种算法的根本区别究竟在哪里？答案藏在协方差更新环节的实现细节中：

% UKF的加权更新
P_new = Q;
for i=1:2*n+1
    P_new = P_new + Wc(i)*(sigma_points(:,i)-xhat)*(sigma_points(:,i)-xhat)';
end

% CKF的积分近似
P_new = 0;
for i=1:2*n
    P_new = P_new + w(i)*(trans_points(:,i)-xhat)*(trans_points(:,i)-xhat)';
end
P_new = P_new + Q;

可以看出，UKF在协方差计算过程中使用两组不同的权重（Wm和Wc），以区分均值与协方差的传播；而CKF则采用等权策略，所有采样点贡献一致。这一设计使得CKF在强非线性动态（如轮胎滑移率骤变）中表现出更强的数值鲁棒性；而UKF由于具备更精细的加权机制，在缓慢变化的过程跟踪方面更具细腻度。

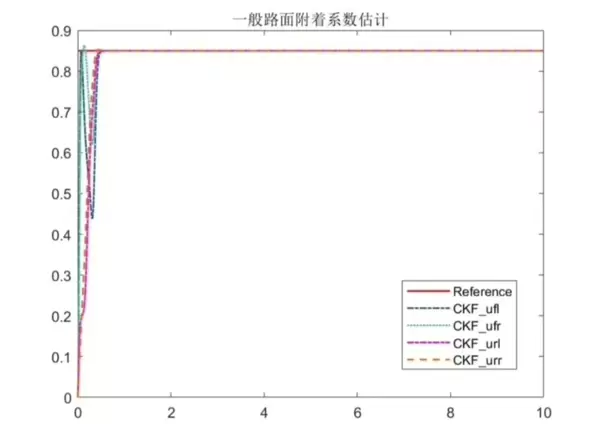
建议在自行开展仿真时，重点关注0.3秒至0.8秒的时间窗口。这一区间往往是附着系数发生突变的关键观测期，也是两种算法性能分化的“分水岭”。在此阶段，CKF的响应如同毛笔晕染，过渡柔和自然；而UKF则类似铅笔勾勒，边界清晰、反应迅速。工程实践中可根据车型定位做出取舍：注重安全稳定的系统可优先选用CKF，追求快速响应的场景则更适合采用UKF。