第一章 你以为 t 检验很简单?
t检验主要用于比较两个来自正态分布总体的均值是否存在显著差异。可用于检验样本均值与已知总体均值差异,也能对比两组独立样本均值,为科学研究和实际决策提供可靠依据。t 检验毫无疑问是最基础的统计分析方法,然而因为简单,在统计分析工作中经常会忽略一些细节导致结果不够严谨,如何将这个最基础的统计分析方法用的无懈可击,将是我们在第一章需要讨论的问题。1 适用场景:比较两组样本均数的差异2 应用条件
2.1 随机样本
t 检验要求来自总体的样本具有随机性,而满足这一要求需要在研究设计阶段通过随机抽样和随机分组的方法实现,然而遗憾的是,大部分的临床工作者所收集的数据来自其工作的医院,因此样本的随机性很难保证,幸运的是,期刊似乎也考虑到了这种情况,对于样本的随机性要求并不严格。但我们并不能因此忽略这一条件,课题项目的研究设计阶段,一定要在课题设计阶段确定科学的数据收集标准,从而提高样本的代表性。
2.2 来自正态分布总计
t 检验要求样本来自服从正态分布的总体,这就要求我们在进行 t 检验之前要对样本进行正态性检验,这也是在 t 检验中各位容易忽视或者产生疑惑的地方,如何进行正态分布,如果数据不服从正态分布怎么办?我将在后文中对这两个问题进行讲解。
2.3 均数比较时,要求两总体方差相等(方差齐性)
两独立样本 t 检验要求两组样本来自的总体方差相等,因此在进行两独立样本 t 检验前,除了正态性检验,还需要对两组样本进行方差齐性检验。值得您注意的是,配对样本 t 检验并不需要这一条件,因为配对样本 t 检验的两组数据来自同一研究总体。
3 案例思考
3.1 数据来源
本章案例采用自行编制的模拟数据,数据模拟了200名糖尿病患者在用药前和用药2年后的(身体质量指数)BMI数据,其中,男性100人,女性100人,分别测量其身高、体重并计算BMI,数据具体情况见下图(考虑到篇幅问题仅展示10个样本):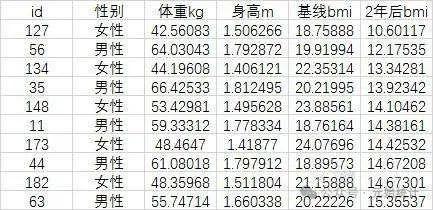
3.2 问题思考:基于这一数据,我们很容易产生如下两个假设:
假设1:男性和女性基线BMI不同
假设2:用药两年后患者的BMI与基线BMI不同
针对以上两个假设,我们开始本章的统计分析。
4 统计分析
4.1 两独立样本 t 检验
针对假设1:男性基线BMI高于女性,很明显,男性和女性糖尿病患者来自不同研究总体,因此,要比较两组样本BMI的差异,我们的脑海里第一个想法便是两独立样本 t 检验,然而,我们的数据是否真的可以进行两独立样本 t 检验呢?这需要我们首先对其适用条件进行检验。
4.1.1 正态性检验
本例中,我们需要对男性和女性的基线BMI分别进行正态性检验,而这也是我们通常会犯的第一个错误,有些研究者会简单地将两组数据(200名患者)整体进行正态性检验,因此出现了第一个错误,下面我们介绍正确的正态性检验方法的SPSS 26.0 操作步骤:
(1)分析→描述统计→探索→将变量“基线BMI”选入“因变量列表”框,将变量“性别”选入“因子列表”框: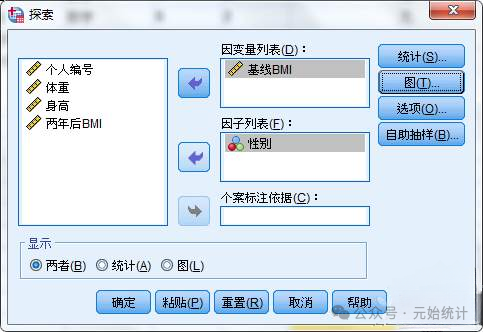
(2)点击“图”按钮→勾选“含检验的正态图”,勾选“含莱文检验的分布-水平图”中的“未转换”选项,其他默认(我将其他不需要的内容都取消了勾选)→点击“继续”按钮返回上一级窗口:
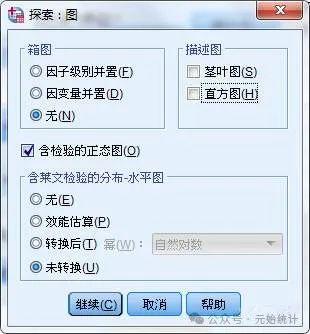
(3)点击“确定”按钮输出结果:
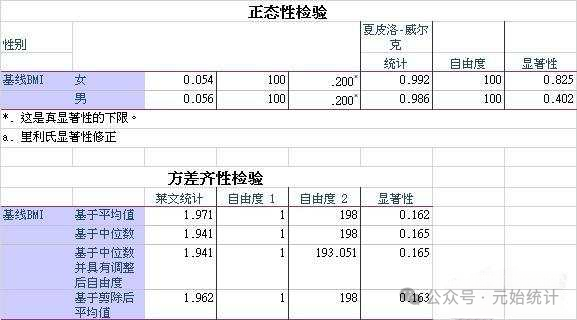
结果解读:第一个表“正态性检验”展示了正态性检验结果,从表中可以看出,女性(p = 0.825)和男性(p = 0.402)的“显著性”均大于0.05,因此说明两组样本均服从正态分布;第二个表“方差齐性检验”展示了方差齐性检验的结果,我们只需要看“基于平均值”这一行的结果,“显著性”=0.162>0.05,说明两组数据方差相等(其实,SPSS软件中我们并不需要单独进行方差齐性检验,在后文你将知道原因)。在确定了我们的样本适用与两独立样本 t 检验后,我们可以开始进行两独立样本 t 检验了。
4.1.2 两独立样本 t 检验
(1)分析→比较平均值→独立样本T检验→将变量“基线BMI”选入“检验变量”框,将变量“性别”选入“分组变量”框:
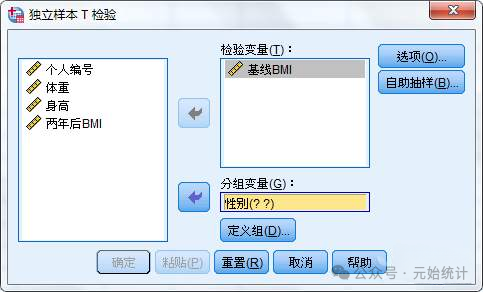
(2)点击“定义组”按钮→勾选“使用指定的值”→对“组1”赋值1(男性),对“组2”赋值0(女性)→点击继续返回上一级窗口:
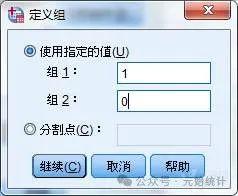
(3)点击“确定”按钮输出结果:
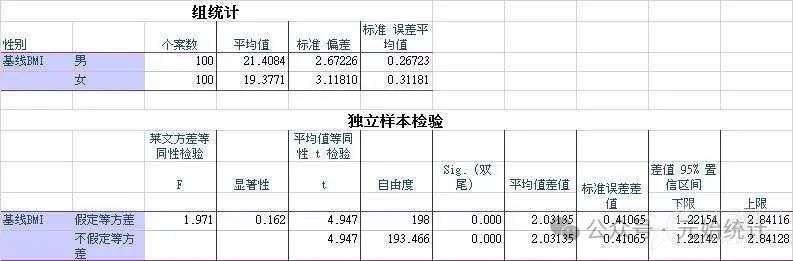
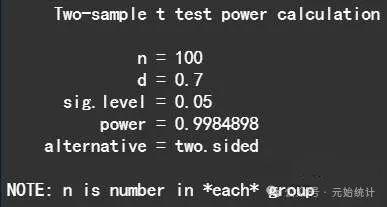
结果解读:功效分析结果显示,当两组样本量相等且n=100,允许误差=0.7,置信度sig.level=0.05且为双侧检验时,功效power=0.998,提示采用两独立样本 t 检验对假设1进行验证具有完美的功效!
4.2 配对样本 t 检验
针对假设2:用药两年后患者的BMI与基线BMI不同,由于患者均来自同一研究总体,因此我们选用配对样本 t 检验对进行假设检验,第一步当然是正态性检验。4.2.1 正态性检验:
(1)转换→计算变量→在“目标变量”框中输入新变量名“BMI差值”→在“数字表达式”框中输入“基线BMI - 两年后BMI”→点击“确定”,生成新变量“BMI差值”:

(2)分析→描述统计→探索→将变量“BMI差值”选入“因变量列表”:
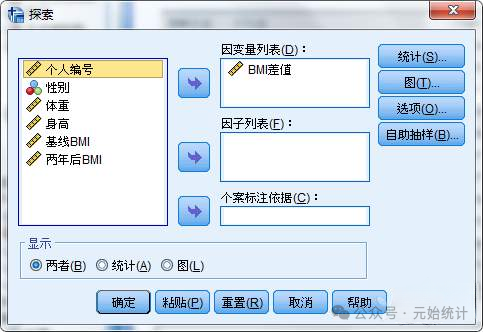
(3)点击“图”按钮→勾选“含检验的正态图”,其他默认→点击“确定”按钮返回上一级窗口:
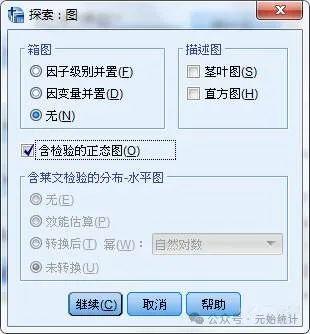
(4)点击“确定”按钮,输出结果:
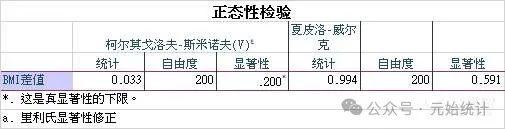
结果解读:正态性检验结果显示,变量“BMI差值”服从正态分布,因此我们继续进行配对样本 t 检验。
4.2.2 配对样本 t 检验:
(1)分析→比较平均值→成对样本T检验→将“基线BMI”选入“变量1”格,将“两年后BMI”选入“变量2”格:
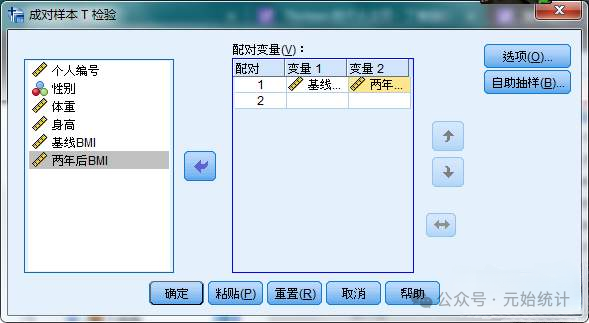
(2)点击“确定”按钮,输出结果:
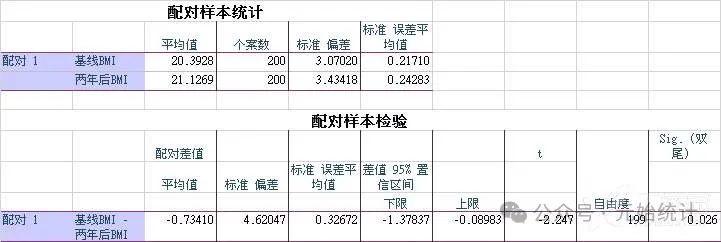
结果解读:第一个表“配对样本统计”展示了“基线BMI”和“两年后BMI”的个案数、平均值和标准偏差,是我们制表所需用到的3个参数;‘第二个表“配对样本检验”展示了检验结果:t=-2.247,p=0.026<0.05,结合“基线BMI”和“两年后BMI”我们可以验证假设2:用药两年后患者的BMI与基线BMI不同。当然还没结束,我们继续进行功效分析:
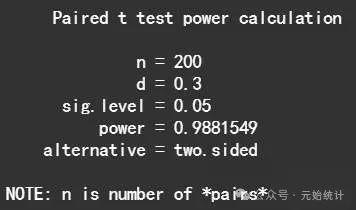
结果解读:功效分析结果显示,当样本量n=200,允许误差=0.3,置信sig.level=0.05且为双侧检验时,功效power=0.988,提示采用配对样本 t 检验对假设2进行验证具有完美的功效!
5 本章总结
5.1 介绍了 t 检验的适用场景和适用条件
5.2 介绍了 t 检验的SPSS 26.0 操作步骤
5.3 介绍了 t 检验的功效分析





 雷达卡
雷达卡






 京公网安备 11010802022788号
京公网安备 11010802022788号







