发帖
雷达卡
130年前，人们知道了平面或者球面至少需要4种颜色染色，因为平面或者球面可以构造4个区域两两相连，3种颜色染色显然是不够的。见下面的图3：
第 二，
A德摩根证明了平面或者球面不可能构造5个区域两两相连，因此，平面或者球面不需要5种颜色染色。
下面图是A德摩根的证明：
第三，
有人构造了下面这个图4：意思是说，6个区域，没有哪4个与其它区域是每一个都和其它3个相连的，仍然需要4种颜色。（就是说，下面的图4，不是每一个区域都两两相连的，还是需要4种颜色）
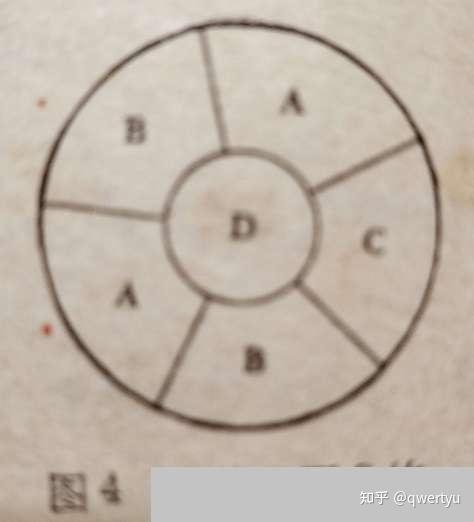
第 四，
于是，100年前的数学家否定了：需要4种颜色染色的4个区域两两相连的平面或者球面，不能5个区域两两相连的平面或者球面，因为图4，否定了”4种颜色染色就足够了“的判断。
第五，
大家看出数学家对上面第三节和第四节的理解出现的错误了吗？
图4中有6个区域，虽然不是4个区域两两相连。我们将第三节的图4染色后，可以发现：
”4种颜色两两相连“。每一种颜色与其它3种颜色两两相连。
我们的命题”平面或者球面的多个区域需要4种颜色染色“；而不是”平面或者球面多个区域需要两两相连“。
问题已经解决了，过去数学家不能将”4个区域“过度到”4种颜色“
第六，非局部性要求
四色定理的表述需强调两点：
全局性：针对整个平面地图的任意划分，而非局部区域数量；
充分性：四种颜色足以覆盖所有可能相邻关系，因平面无法构造五个两两相连区域。
误解常源于将“两两相连”局限于特定数量的区域，而忽略定理对整体结构的约束。
京公网安备 11010802022788号
