当前广泛采用的室外定位方法,通过多颗卫星信号确定位置,主要系统包括美国的GPS、中国的北斗、俄罗斯的GLONASS和欧盟的Galileo。这些系统的中心定位原理大致相同,但在星座配置、信号频段等方面各具特色。本文将基于GPS技术,从基本原理到优缺点详述人员定位系统的实现,并提供一些实用建议。
一、GPS在人员定位系统中的应用原理
基本原则:卫星距离测量和三角定位,通过接收卫星信号计算人员的实际位置。
手机等终端需接收到至少4颗卫星的信号,利用“时间差”来确定与卫星的距离,并结合卫星的位置信息反推出自身的确切位置。在常规环境下精度通常为1-5米,遇到遮挡或干扰时误差可能超过10米。要达到厘米级的专业精度,则需要借助GNSS增强技术,主要应用于自动驾驶、精准农业等领域,在此不作详述。
基本流程是发射-接收-计算-解算的逐步推进,具体步骤如下:
- 卫星发送信号:GPS卫星不断广播自身位置、时间戳(精确的时间数据)等信息,并以光速传播。
- 终端接收信号:人员佩戴的GPS设备(如定位手环、工牌、智能手机等),同时接收到至少4颗卫星的信号。
- 距离计算:通过分析信号传输时间差,计算每个卫星的距离。
- 位置解算:利用多个卫星的位置数据,通过三角测量法推导出人员的经纬度、海拔高度等具体信息。
此外,实现精准定位还需要一些关键技术的支持:
- 距离计算的核心是确保卫星与终端设备时间的精确同步;
- 多卫星冗余:接收至少4颗卫星信号有助于校正误差,提高定位精度;
- 误差修正:通过差分GPS(DGPS)等技术减少电离层对信号的影响、卫星时钟偏差等问题。
误差修正段代码
import numpy as np
from typing import List, Tuple
class DGPS_Core:
"""差分GPS(DGPS)核心类:专注于误差修正逻辑(电离层干扰、卫星钟差抵消)"""
def __init__(self):
self.c = 299792458.0 # 光速 [m/s]
def generate_satellite_signals(self,
satellites_pos: List[np.ndarray],
receiver_true_pos: np.ndarray,
base_true_pos: np.ndarray) -> Tuple[List[float], List[float], List[float]]:
"""
生成含误差的卫星信号(伪距):模拟真实场景中的误差源
误差组成:卫星钟差 + 电离层干扰 + 随机噪声
返回:终端伪距、基站伪距、真实伪距(无误差基准)
"""
terminal_pseudoranges = [] # 终端接收的伪距(含所有误差)
base_pseudoranges = [] # 基站接收的伪距(含公共误差,无终端钟差)
true_pseudoranges = [] # 真实伪距(无任何误差,用于对比)
# 生成公共误差(所有接收机共享:卫星钟差、电离层干扰)
num_sats = len(satellites_pos)
sat_clock_biases = np.random.normal(0, 8e-9, num_sats) # 卫星钟差(0-2.4m距离误差)
iono_errors = np.random.normal(0, 6, num_sats) # 电离层干扰(0-6m误差)
common_noise = np.random.normal(0, 0.5, num_sats) # 公共随机噪声(0-0.5m)
# 生成终端独有误差(终端钟差)
terminal_clock_bias = np.random.normal(0, 1e-8) # 终端钟差(0-3m距离误差)
for i in range(num_sats):
sat_pos = satellites_pos[i]
# 1. 计算真实几何距离(终端-卫星、基站-卫星)
true_dist_terminal = np.linalg.norm(sat_pos - receiver_true_pos)
true_dist_base = np.linalg.norm(sat_pos - base_true_pos)
# 2. 真实伪距(无任何误差)
true_pr = true_dist_terminal
true_pseudoranges.append(true_pr)
# 3. 终端伪距(含所有误差:公共误差 + 终端独有误差)
terminal_pr = (true_dist_terminal
+ sat_clock_bias[i] * self.c # 卫星钟差贡献
- terminal_clock_bias * self.c # 终端钟差贡献(伪距公式特性)
+ iono_errors[i] # 电离层干扰
+ common_noise[i]) # 公共噪声
terminal_pseudoranges.append(terminal_pr)
# 4. 基站伪距(含公共误差,无终端误差:基站钟差已精确校准)
base_pr = (true_dist_base
+ sat_clock_bias[i] * self.c # 卫星钟差贡献
+ iono_errors[i] # 电离层干扰
+ common_noise[i]) # 公共噪声
base_pseudoranges.append(base_pr)
return terminal_pseudoranges, base_pseudoranges, true_pseudoranges
def dgps_correct(self,
terminal_pr: List[float],
base_pr: List[float],
base_true_pos: np.ndarray,
satellites_pos: List[np.ndarray]) -> List[float]:
"""
DGPS核心修正逻辑:抵消公共误差(卫星钟差、电离层干扰等)
原理:基站已知真实位置,可计算“公共误差值”,终端通过差分抵消该误差
"""
corrected_pr = []
num_sats = len(satellites_pos)
for i in range(num_sats):
# 步骤1:计算基站的“真实伪距”(已知基站位置,无误差)
base_true_dist = np.linalg.norm(satellites_pos[i] - base_true_pos)
base_true_pr = base_true_dist # 基站无钟差,真实伪距=真实距离
# 步骤2:计算基站的“误差量”(基站伪距 - 基站真实伪距 = 公共误差)
base_error = base_pr[i] - base_true_pr # 包含卫星钟差、电离层、公共噪声
# 步骤3:终端伪距减去公共误差 → 抵消误差后的修正伪距
# 核心逻辑:终端和基站受同一套公共误差影响,差分可直接抵消
corrected_pr_i = terminal_pr[i] - base_error
corrected_pr.append(corrected_pr_i)
return corrected_pr
def calculate_position_error(self,
pseudoranges: List[float],
satellites_pos: List[np.ndarray],
true_pos: np.ndarray) -> float:
"""
基于伪距解算终端位置,并计算定位误差(最小二乘法)
用于验证DGPS修正前后的精度提升
"""
if len(satellites_pos) < 4:
raise ValueError("DGPS需要至少4颗卫星实现定位解算(当前卫星数:{})".format(len(satellites_pos)))
# 构建最小二乘方程组,求解位置(x,y,z)和钟差(dt)
A = []
b = []
x0 = np.hstack([satellites_pos[0], 0.0]) # 初始估计(第一颗卫星位置+钟差=0)
# 迭代求解(2-3次收敛)
for _ in range(3):
A.clear()
b.clear()
for i in range(len(satellites_pos)):
sat_pos = satellites_pos[i]
est_dist = np.linalg.norm(sat_pos - x0[:3])
if est_dist < 1e-6:
est_dist = 1e-6
# 方向余弦(单位向量)
cos_x = (sat_pos[0] - x0[0]) / est_dist
cos_y = (sat_pos[1] - x0[1]) / est_dist
cos_z = (sat_pos[2] - x0[2]) / est_dist
# 方程组系数和右边项
A.append([cos_x, cos_y, cos_z, self.c])
b_i = pseudoranges[i] - (est_dist - self.c * x0[3])
b.append(b_i)
# 最小二乘求解
A = np.array(A)
b = np.array(b).reshape(-1, 1)
delta_x = np.linalg.inv(A.T @ A) @ A.T @ b
estimated_pos = x0[:3] + delta_x[:3].flatten()
# 计算定位误差(欧氏距离)
position_error = np.linalg.norm(estimated_pos - true_pos)
return position_error, estimated_pos
# ------------------------------ 仿真验证:DGPS误差修正效果 ------------------------------
if __name__ == "__main__":
# 1. 配置仿真参数
dgps_core = DGPS_Core()
# 终端真实位置(例如:北纬30°附近的平面坐标转换后)[单位:m]
receiver_true_pos = np.array([350000.0, 550000.0, 12000.0])
# DGPS基站位置(已知精确位置,与终端距离较近,共享相同公共误差)[单位:m]
base_true_pos = np.array([350150.0, 550200.0, 12000.0])
# 5颗GPS卫星轨道位置(模拟中地球轨道MEO)[单位:m]
satellites_pos = [
np.array([20100000.0, 15200000.0, 10300000.0]),
np.array([18400000.0, 12600000.0, 14700000.0]),
np.array([22200000.0, 18800000.0, 8500000.0]),
np.array([19600000.0, 16300000.0, 12200000.0]),
np.array([21400000.0, 14100000.0, 11600000.0])
]
# 2. 生成含误差的伪距
terminal_pr, base_pr, true_pr = dgps_core.generate_satellite_signals(
satellites_pos=satellites_pos,
receiver_true_pos=receiver_true_pos,
base_true_pos=base_true_pos
)
# 3. 对比修正前后的伪距误差
print("="*60)
print("DGPS修正前后 伪距误差对比(单颗卫星)")
print("="*60)
for i in range(3): # 打印前3颗卫星的伪距误差
raw_error = abs(terminal_pr[i] - true_pr[i]) # 修正前伪距误差
corrected_pr_temp = dgps_core.dgps_correct([terminal_pr[i]], [base_pr[i]], base_true_pos, [satellites_pos[i]])[0]
corrected_error = abs(corrected_pr_temp - true_pr[i]) # 修正后伪距误差
print(f"卫星{i+1}:")
print(f" 修正前伪距误差:{raw_error:.2f} m(含卫星钟差+电离层干扰)")
print(f" 修正后伪距误差:{corrected_error:.2f} m(抵消公共误差)")
print()
# 4. 定位解算:对比修正前后的定位精度
print("="*60)
print("DGPS修正前后 定位精度对比")
print("="*60)
# 修正前定位
raw_pos_error, raw_est_pos = dgps_core.calculate_position_error(
pseudoranges=terminal_pr,
satellites_pos=satellites_pos,
true_pos=receiver_true_pos
)
# 修正后定位
corrected_pr = dgps_core.dgps_correct(terminal_pr, base_pr, base_true_pos, satellites_pos)
corrected_pos_error, corrected_est_pos = dgps_core.calculate_position_error(
pseudoranges=corrected_pr,
satellites_pos=satellites_pos,
true_pos=receiver_true_pos
)
# 打印结果
print(f"终端真实位置:{np.round(receiver_true_pos, 2)}")
print(f"修正前估计位置:{np.round(raw_est_pos, 2)}")
print(f"修正前定位误差:{raw_pos_error:.2f} m")
print(f"\n修正后估计位置:{np.round(corrected_est_pos, 2)}")
print(f"修正后定位误差:{corrected_pos_error:.2f} m")
print(f"\nDGPS误差修正效果:定位误差降低 {((raw_pos_error - corrected_pos_error)/raw_pos_error * 100):.1f}%")
# 5. 核心结论
print("\n" + "="*60)
print("核心结论:")
print("1. DGPS通过基站与终端的伪距差分,抵消了卫星钟差、电离层干扰等公共误差")
print("2. 修正后定位误差从数米级降至亚米级(仿真中通常<1m)")
print("3. 关键前提:基站与终端距离较近(共享相同公共误差)、基站位置已知且精确")最后,终端设备将计算出的位置数据通过移动网络(4G/5G)、WiFi等方式上传到后台系统。后台处理这些数据后,以地图形式直观显示人员的实时位置,并提供轨迹回放等系统功能。
二、GPS人员定位系统的功能展示
- 实现实时精确定位:使用定位技术对场景内的人员进行即时定位,在电子地图上精准呈现这些对象的位置。点击地图中的定位标记可查看相关详细信息,如部门、姓名、电话等;通过不同的图标或颜色来区分不同类型的工作人员。
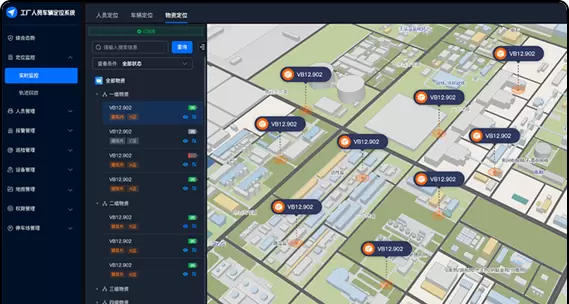
- 电子点名管理:在任意区域内动态统计人数,实时监控人员的在线状态、休眠和离线情况。
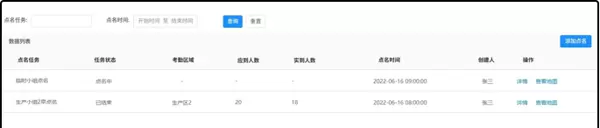
- 历史轨迹回溯:选择特定人员,自由设定回放日期和速度,即可查询其活动路径;同时可以在路径中查看各点的时间记录。根据这些历史轨迹进行岗位监督,确保工作流程符合管理规范。
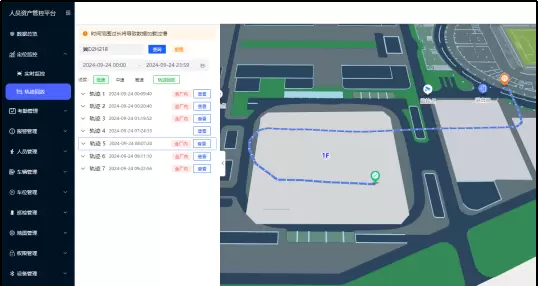
- 智能考勤打卡:预先设置地理围栏作为考勤区域,自动记录人员进出时间,生成早退、滞留或缺勤等报表。在系统中设定考勤范围,当员工进入该区域时,自动记录区域名称和出入时间及停留期间的长短,后台自动生成考勤报表,实现无感知自动化考勤。
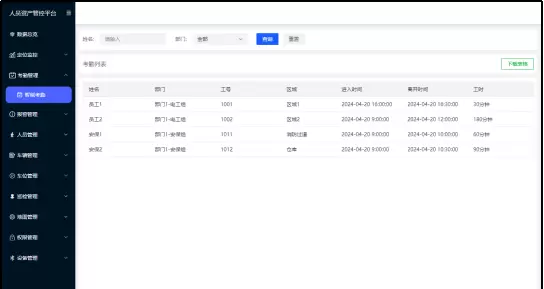
希望本文对您有所帮助。由于篇幅限制,关于优缺点和避坑指南的内容将安排在下一篇文章中:GPS 人员定位系统:原理拆解 + 优劣分析 + 避坑指南(二)。




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







