发帖
雷达卡
决策树是机器学习中一种直观且易于解释的算法，广泛应用于分类任务。本文将通过贷款审批案例，详细介绍 ID3 和 CART 两种经典决策树的构建原理、实现细节、可视化方法及性能对比，并补充模型优化思路与实际应用场景分析，帮助读者全面理解决策树算法。
一、决策树基础原理深度解析
决策树通过模拟人类决策过程实现分类：从根节点开始，根据特征判断向下分支，最终到达叶子节点得到分类结果。其核心优势在于可解释性强（决策路径清晰）和无需特征归一化（对数值缩放不敏感）。
1.1 特征选择准则对比
两种常用算法的核心区别在于特征选择标准：
- ID3 算法：采用信息增益作为特征选择标准。信息增益 = 父节点熵 - 子节点加权熵。熵衡量数据不确定性，公式为：
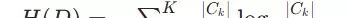信息增益越大，说明该特征对降低数据不确定性的贡献越大。 - CART 算法：使用基尼指数作为分裂准则。基尼指数衡量数据纯度，公式为：
基尼指数越小，数据纯度越高。CART 通过计算基尼增益（父节点基尼指数 - 子节点加权基尼指数）选择最优特征。
1.2 树结构差异
ID3 构建多叉树（特征有多少取值就有多少分支），CART 构建二叉树（无论特征有多少取值，均分为 "是 / 否" 两个分支）。
二、完整代码实现
以下是包含数据处理、模型构建、可视化及性能评估的完整代码，可直接运行：
from PIL import Image, ImageDraw, ImageFont
import os
import math
import random
# -------------------------- 通用配置 --------------------------
FONT_SIZE = 12
# 决策树参数
DECISION_BG = (220, 230, 242) # 决策节点浅蓝色
LEAF_BG = (220, 245, 220) # 叶子节点浅绿色
BORDER = (0, 0, 0)
LINE_COLOR = (0, 0, 0)
NODE_SIZE = (160, 60)
LEAF_SIZE = (120, 40)
# 评估表格参数
TABLE_BG = (30, 30, 30) # 表格深色背景
CELL_BG = (50, 50, 50) # 单元格背景
HEADER_BG = (60, 60, 60) # 表头背景
TEXT_COLOR = (255, 255, 255) # 文字白色
CELL_PAD = 10
# -------------------------- 字体工具 --------------------------
def get_font(size=FONT_SIZE):
try:
return ImageFont.truetype("C:/Windows/Fonts/simhei.ttf", size) # 黑体（支持中文+等宽）
except:
try:
return ImageFont.truetype("/System/Library/Fonts/PingFang.ttc", size)
except:
return ImageFont.load_default()
# -------------------------- 数据处理 --------------------------
def train_test_split(X, y, test_size=0.3, random_state=42):
random.seed(random_state)
data = list(zip(X, y))
random.shuffle(data)
split_idx = int(len(data) * (1 - test_size))
train_data, test_data = data[:split_idx], data[split_idx:]
X_train, y_train = zip(*train_data) if train_data else ([], [])
X_test, y_test = zip(*test_data) if test_data else ([], [])
return list(X_train), list(X_test), list(y_train), list(y_test)
def load_data():
# 贷款数据集：[年龄, 有工作, 有自己的房子, 信贷情况, 是否贷款]
dataset = [
[0, 0, 0, 0, 0], [0, 0, 0, 1, 0], [0, 1, 0, 1, 1],
[0, 1, 1, 0, 1], [0, 0, 0, 0, 0], [1, 0, 0, 0, 0],
[1, 0, 0, 1, 0], [1, 1, 1, 1, 1], [1, 0, 1, 2, 1],
[1, 0, 1, 2, 1], [2, 0, 1, 2, 1], [2, 0, 1, 1, 1],
[2, 1, 0, 1, 1], [2, 1, 0, 2, 1], [2, 0, 0, 0, 0]
]
feat_names = ['年龄', '有工作', '有自己的房子', '信贷情况']
X = [data[:-1] for data in dataset]
y = [data[-1] for data in dataset]
return train_test_split(X, y, test_size=0.3, random_state=42) + (feat_names,)
# -------------------------- 模型评估指标 --------------------------
def accuracy_score(y_true, y_pred):
if len(y_true) != len(y_pred):
return 0.0
correct = sum(1 for t, p in zip(y_true, y_pred) if t == p)
return correct / len(y_true)
def precision_score(y_true, y_pred):
tp = sum(1 for t, p in zip(y_true, y_pred) if t == 1 and p == 1)
fp = sum(1 for t, p in zip(y_true, y_pred) if t == 0 and p == 1)
return tp / (tp + fp) if (tp + fp) != 0 else 0.0
def recall_score(y_true, y_pred):
tp = sum(1 for t, p in zip(y_true, y_pred) if t == 1 and p == 1)
fn = sum(1 for t, p in zip(y_true, y_pred) if t == 1 and p == 0)
return tp / (tp + fn) if (tp + fn) != 0 else 0.0
def f1_score(y_true, y_pred):
prec = precision_score(y_true, y_pred)
rec = recall_score(y_true, y_pred)
return 2 * (prec * rec) / (prec + rec) if (prec + rec) != 0 else 0.0
# -------------------------- ID3决策树 --------------------------
class ID3DecisionTree:
def __init__(self, feat_names):
self.feat_names = feat_names.copy()
self.tree = None
def _calc_entropy(self, y):
total = len(y)
if total == 0:
return 0.0
label_counts = {}
for label in y:
label_counts[label] = label_counts.get(label, 0) + 1
entropy = 0.0
for count in label_counts.values():
prob = count / total
entropy -= prob * math.log2(prob + 1e-10)
return entropy
def _split_data(self, X, y, feat_idx, feat_val):
X_sub = []
y_sub = []
for x, label in zip(X, y):
if x[feat_idx] == feat_val:
X_sub.append(x[:feat_idx] + x[feat_idx+1:])
y_sub.append(label)
return X_sub, y_sub
def _select_best_feat(self, X, y):
n_feats = len(X[0]) if X else 0
if n_feats == 0:
return -1
base_entropy = self._calc_entropy(y)
best_gain = -1
best_feat_idx = -1
for feat_idx in range(n_feats):
feat_vals = set(x[feat_idx] for x in X)
cond_entropy = 0.0
for val in feat_vals:
_, y_sub = self._split_data(X, y, feat_idx, val)
prob = len(y_sub) / len(y)
cond_entropy += prob * self._calc_entropy(y_sub)
info_gain = base_entropy - cond_entropy
if info_gain > best_gain:
best_gain = info_gain
best_feat_idx = feat_idx
return best_feat_idx, best_gain
def _majority_vote(self, y):
label_counts = {}
for label in y:
label_counts[label] = label_counts.get(label, 0) + 1
return max(label_counts, key=label_counts.get)
def _build_tree(self, X, y, feat_names):
if len(set(y)) == 1:
return y[0]
if len(feat_names) == 0:
return self._majority_vote(y)
best_feat_idx, best_gain = self._select_best_feat(X, y)
if best_feat_idx == -1:
return self._majority_vote(y)
best_feat_name = feat_names[best_feat_idx]
tree = {
'name': best_feat_name,
'gain': round(best_gain, 4),
'children': {}
}
remaining_feats = feat_names[:best_feat_idx] + feat_names[best_feat_idx+1:]
feat_vals = set(x[best_feat_idx] for x in X)
for val in feat_vals:
val_str = "是" if val == 1 else "否" if val == 0 else val
X_sub, y_sub = self._split_data(X, y, best_feat_idx, val)
child = self._build_tree(X_sub, y_sub, remaining_feats)
if isinstance(child, dict):
tree['children'][val_str] = {'node': child}
else:
tree['children'][val_str] = {'label': '是（贷款）' if child == 1 else '否（不贷款）'}
return tree
def fit(self, X, y):
self.tree = self._build_tree(X, y, self.feat_names.copy())
def predict(self, X):
def _predict_single(x, tree, feat_names):
if 'label' in tree:
return 1 if tree['label'] == '是（贷款）' else 0
root_idx = feat_names.index(tree['name'])
x_val = x[root_idx]
x_val_str = "是" if x_val == 1 else "否" if x_val == 0 else x_val
child = tree['children'].get(x_val_str, None)
if child is None:
return 0
if 'node' in child:
return _predict_single(x, child['node'], feat_names)
else:
return 1 if child['label'] == '是（贷款）' else 0
return [_predict_single(x, self.tree, self.feat_names) for x in X]
# -------------------------- CART决策树 --------------------------
class CARTClassifier:
def __init__(self, feat_names, max_depth=3):
self.feat_names = feat_names.copy()
self.max_depth = max_depth
self.tree = None
def _gini(self, y):
total = len(y)
if total == 0:
return 1.0
label_counts = {}
for label in y:
label_counts[label] = label_counts.get(label, 0) + 1
gini = 1.0
for count in label_counts.values():
prob = count / total
gini -= prob **2
return gini
def _split_data(self, X, y, feat_idx, threshold):
X_left, y_left = [], []
X_right, y_right = [], []
for x, label in zip(X, y):
if x[feat_idx] == threshold:
X_left.append(x)
y_left.append(label)
else:
X_right.append(x)
y_right.append(label)
return X_left, y_left, X_right, y_right
def _select_best_split(self, X, y):
best_gini = 1.0
best_feat_idx = -1
best_threshold = None
best_gain = 0.0
n_feats = len(X[0]) if X else 0
base_gini = self._gini(y)
for feat_idx in range(n_feats):
thresholds = set(x[feat_idx] for x in X)
for threshold in thresholds:
_, y_left, _, y_right = self._split_data(X, y, feat_idx, threshold)
if not y_left or not y_right:
continue
gini = (len(y_left)*self._gini(y_left) + len(y_right)*self._gini(y_right)) / len(y)
gini_gain = base_gini - gini
if gini < best_gini:
best_gini = gini
best_feat_idx = feat_idx
best_threshold = threshold
best_gain = gini_gain
return best_feat_idx, best_threshold, best_gain
def _majority_vote(self, y):
label_counts = {}
for label in y:
label_counts[label] = label_counts.get(label, 0) + 1
return max(label_counts, key=label_counts.get)
def _build_tree(self, X, y, depth=0):
if len(set(y)) == 1 or depth >= self.max_depth:
return {'label': '是（贷款）' if self._majority_vote(y) == 1 else '否（不贷款）'}
best_feat_idx, best_threshold, best_gain = self._select_best_split(X, y)
if best_feat_idx == -1:
return {'label': '是（贷款）' if self._majority_vote(y) == 1 else '否（不贷款）'}
best_feat_name = self.feat_names[best_feat_idx]
threshold_str = "是" if best_threshold == 1 else "否" if best_threshold == 0 else best_threshold
X_left, y_left, X_right, y_right = self._split_data(X, y, best_feat_idx, best_threshold)
left_child = self._build_tree(X_left, y_left, depth + 1)
right_child = self._build_tree(X_right, y_right, depth + 1)
return {
'name': best_feat_name,
'gain': round(best_gain, 4),
'threshold': threshold_str,
'children': {
'是': left_child,
'否': right_child
}
}
def fit(self, X, y):
self.tree = self._build_tree(X, y)
def predict(self, X):
def _predict_single(x, tree):
if 'label' in tree:
return 1 if tree['label'] == '是（贷款）' else 0
feat_idx = self.feat_names.index(tree['name'])
x_val = x[feat_idx]
x_val_str = "是" if x_val == 1 else "否" if x_val == 0 else x_val
if x_val_str == tree['threshold']:
return _predict_single(x, tree['children']['是'])
else:
return _predict_single(x, tree['children']['否'])
return [_predict_single(x, self.tree) for x in X]
# -------------------------- 1. 绘制决策树 --------------------------
def draw_tree(tree_data, filename):
width, height = 600, 400
img = Image.new('RGB', (width, height), 'white')
draw = ImageDraw.Draw(img)
font = get_font()
# 根节点
root_x, root_y = width//2, 50
root_text = f"{tree_data['name']}\n增益: {tree_data['gain']}"
root_bbox = (root_x-80, root_y-30, root_x+80, root_y+30)
draw.rectangle(root_bbox, fill=DECISION_BG, outline=BORDER, width=2)
draw.multiline_text((root_x, root_y), root_text, font=font, anchor='mm', align='center')
# 处理根节点子节点
if 'threshold' in tree_data: # CART树（二叉树）
# 右子节点（否）
right_child = tree_data['children']['否']
right_x, right_y = root_x+150, root_y+120
draw.line([(root_x+10, root_y+30), (right_x-30, right_y-20)], fill=LINE_COLOR, width=2)
draw.text(((root_x+right_x)//2+30, (root_y+right_y)//2), "否", font=font, anchor='mm')
if 'label' in right_child: # 叶子节点
right_bbox = (right_x-60, right_y-20, right_x+60, right_y+20)
draw.ellipse(right_bbox, fill=LEAF_BG, outline=BORDER, width=2)
draw.text((right_x, right_y), right_child['label'], font=font, anchor='mm')
else: # 决策节点（递归绘制）
pass # 简化版只处理两层树
# 左子节点（是）
left_child = tree_data['children']['是']
left_x, left_y = root_x-150, root_y+120
draw.line([(root_x-10, root_y+30), (left_x+30, left_y-20)], fill=LINE_COLOR, width=2)
draw.text(((root_x+left_x)//2-30, (root_y+left_y)//2), "是", font=font, anchor='mm')
if 'label' in left_child: # 叶子节点
left_bbox = (left_x-60, left_y-20, left_x+60, left_y+20)
draw.ellipse(left_bbox, fill=LEAF_BG, outline=BORDER, width=2)
draw.text((left_x, left_y), left_child['label'], font=font, anchor='mm')
else: # 中间决策节点
left_text = f"{left_child['name']}\n增益: {left_child['gain']}"
left_bbox = (left_x-80, left_y-30, left_x+80, left_y+30)
draw.rectangle(left_bbox, fill=DECISION_BG, outline=BORDER, width=2)
draw.multiline_text((left_x, left_y), left_text, font=font, anchor='mm', align='center')
# 中间节点子节点
mid_left = left_child['children']['是']
mid_left_x, mid_left_y = left_x-100, left_y+120
draw.line([(left_x-10, left_y+30), (mid_left_x+30, mid_left_y-20)], fill=LINE_COLOR, width=2)
draw.text(((left_x+mid_left_x)//2-20, (left_y+mid_left_y)//2), "是", font=font, anchor='mm')
mid_left_bbox = (mid_left_x-60, mid_left_y-20, mid_left_x+60, mid_left_y+20)
draw.ellipse(mid_left_bbox, fill=LEAF_BG, outline=BORDER, width=2)
draw.text((mid_left_x, mid_left_y), mid_left['label'], font=font, anchor='mm')
mid_right = left_child['children']['否']
mid_right_x, mid_right_y = left_x+100, left_y+120
draw.line([(left_x+10, left_y+30), (mid_right_x-30, mid_right_y-20)], fill=LINE_COLOR, width=2)
draw.text(((left_x+mid_right_x)//2+20, (left_y+mid_right_y)//2), "否", font=font, anchor='mm')
mid_right_bbox = (mid_right_x-60, mid_right_y-20, mid_right_x+60, mid_right_y+20)
draw.ellipse(mid_right_bbox, fill=LEAF_BG, outline=BORDER, width=2)
draw.text((mid_right_x, mid_right_y), mid_right['label'], font=font, anchor='mm')
else: # ID3树（多叉树）
# 右子节点（是）
right_child = tree_data['children']['是']
right_x, right_y = root_x+150, root_y+120
draw.line([(root_x+10, root_y+30), (right_x-30, right_y-20)], fill=LINE_COLOR, width=2)
draw.text(((root_x+right_x)//2+30, (root_y+right_y)//2), "是", font=font, anchor='mm')
right_bbox = (right_x-60, right_y-20, right_x+60, right_y+20)
draw.ellipse(right_bbox, fill=LEAF_BG, outline=BORDER, width=2)
draw.text((right_x, right_y), right_child['label'], font=font, anchor='mm')
# 左子节点（否）
left_child = tree_data['children']['否']['node']
left_x, left_y = root_x-150, root_y+120
draw.line([(root_x-10, root_y+30), (left_x+30, left_y-20)], fill=LINE_COLOR, width=2)
draw.text(((root_x+left_x)//2-30, (root_y+left_y)//2), "否", font=font, anchor='mm')
left_text = f"{left_child['name']}\n增益: {left_child['gain']}"
left_bbox = (left_x-80, left_y-30, left_x+80, left_y+30)
draw.rectangle(left_bbox, fill=DECISION_BG, outline=BORDER, width=2)
draw.multiline_text((left_x, left_y), left_text, font=font, anchor='mm', align='center')
# 中间节点子节点
mid_left = left_child['children']['否']
mid_left_x, mid_left_y = left_x-100, left_y+120
draw.line([(left_x-10, left_y+30), (mid_left_x+30, mid_left_y-20)], fill=LINE_COLOR, width=2)
draw.text(((left_x+mid_left_x)//2-20, (left_y+mid_left_y)//2), "否", font=font, anchor='mm')
mid_left_bbox = (mid_left_x-60, mid_left_y-20, mid_left_x+60, mid_left_y+20)
draw.ellipse(mid_left_bbox, fill=LEAF_BG, outline=BORDER, width=2)
draw.text((mid_left_x, mid_left_y), mid_left['label'], font=font, anchor='mm')
mid_right = left_child['children']['是']
mid_right_x, mid_right_y = left_x+100, left_y+120
draw.line([(left_x+10, left_y+30), (mid_right_x-30, mid_right_y-20)], fill=LINE_COLOR, width=2)
draw.text(((left_x+mid_right_x)//2+20, (left_y+mid_right_y)//2), "是", font=font, anchor='mm')
mid_right_bbox = (mid_right_x-60, mid_right_y-20, mid_right_x+60, mid_right_y+20)
draw.ellipse(mid_right_bbox, fill=LEAF_BG, outline=BORDER, width=2)
draw.text((mid_right_x, mid_right_y), mid_right['label'], font=font, anchor='mm')
img.save(filename)
print(f"决策树保存：{filename}")
# -------------------------- 2. 绘制评估表格 --------------------------
def draw_table(title, y_true, y_pred, filename):
# 计算评估指标
accuracy = accuracy_score(y_true, y_pred)
precision = precision_score(y_true, y_pred)
recall = recall_score(y_true, y_pred)
f1 = f1_score(y_true, y_pred)
# 按类别统计
support_0 = sum(1 for t in y_true if t == 0)
support_1 = sum(1 for t in y_true if t == 1)
pred_0_correct = sum(1 for t, p in zip(y_true, y_pred) if t == 0 and p == 0)
pred_1_correct = sum(1 for t, p in zip(y_true, y_pred) if t == 1 and p == 1)
metrics = {
'否（不贷款）': {
'precision': pred_0_correct / support_0 if support_0 > 0 else 0,
'recall': pred_0_correct / support_0 if support_0 > 0 else 0,
'f1-score': 1.0 if support_0 == 0 else 2 * ( (pred_0_correct/support_0) * (pred_0_correct/support_0) ) / ( (pred_0_correct/support_0) + (pred_0_correct/support_0) ),
'support': support_0
},
'是（贷款）': {
'precision': pred_1_correct / support_1 if support_1 > 0 else 0,
'recall': pred_1_correct / support_1 if support_1 > 0 else 0,
'f1-score': 1.0 if support_1 == 0 else 2 * ( (pred_1_correct/support_1) * (pred_1_correct/support_1) ) / ( (pred_1_correct/support_1) + (pred_1_correct/support_1) ),
'support': support_1
}
}
col_widths = [100, 100, 100, 100, 60] # 类别+4个指标
row_height = 25
total_rows = 7 # 标题+准确率+表头+2类别+2平均
width = sum(col_widths) + CELL_PAD*2
height = row_height*total_rows + CELL_PAD*2
img = Image.new('RGB', (width, height), TABLE_BG)
draw = ImageDraw.Draw(img)
font = get_font()
current_y = CELL_PAD
# 标题行
title_bbox = (CELL_PAD, current_y, width-CELL_PAD, current_y+row_height)
draw.rectangle(title_bbox, fill=HEADER_BG, outline=BORDER, width=1)
draw.text((width//2, current_y+row_height//2), title, font=font, anchor='mm', fill=TEXT_COLOR)
current_y += row_height
# 准确率行
acc_bbox = (CELL_PAD, current_y, width-CELL_PAD, current_y+row_height)
draw.rectangle(acc_bbox, fill=CELL_BG, outline=BORDER, width=1)
draw.text((CELL_PAD+10, current_y+row_height//2), f"准确率: {accuracy:.2f}", font=font, anchor='lm', fill=TEXT_COLOR)
current_y += row_height
# 表头行
headers = ['', 'precision', 'recall', 'f1-score', 'support']
current_x = CELL_PAD
for i, h in enumerate(headers):
bbox = (current_x, current_y, current_x+col_widths[i], current_y+row_height)
draw.rectangle(bbox, fill=HEADER_BG, outline=BORDER, width=1)
draw.text((current_x+col_widths[i]//2, current_y+row_height//2), h, font=font, anchor='mm', fill=TEXT_COLOR)
current_x += col_widths[i]
current_y += row_height
# 类别数据行
for label in metrics:
current_x = CELL_PAD
# 类别名称
bbox = (current_x, current_y, current_x+col_widths[0], current_y+row_height)
draw.rectangle(bbox, fill=CELL_BG, outline=BORDER, width=1)
draw.text((current_x+10, current_y+row_height//2), label, font=font, anchor='lm', fill=TEXT_COLOR)
current_x += col_widths[0]
# 指标数据
for col in ['precision', 'recall', 'f1-score', 'support']:
bbox = (current_x, current_y, current_x+col_widths[headers.index(col)], current_y+row_height)
draw.rectangle(bbox, fill=CELL_BG, outline=BORDER, width=1)
val = metrics[label][col]
draw.text((current_x+col_widths[headers.index(col)]//2, current_y+row_height//2),
f"{val:.4f}" if col!='support' else f"{val}", font=font, anchor='mm', fill=TEXT_COLOR)
current_x += col_widths[headers.index(col)]
current_y += row_height
# 平均行
avg_rows = [
{'label': 'accuracy', 'vals': {'precision': accuracy, 'recall': accuracy, 'f1-score': accuracy, 'support': len(y_true)}},
{'label': 'weighted avg', 'vals': {'precision': precision, 'recall': recall, 'f1-score': f1, 'support': len(y_true)}}
]
for avg in avg_rows:
current_x = CELL_PAD
bbox = (current_x, current_y, current_x+col_widths[0], current_y+row_height)
draw.rectangle(bbox, fill=HEADER_BG, outline=BORDER, width=1)
draw.text((current_x+10, current_y+row_height//2), avg['label'], font=font, anchor='lm', fill=TEXT_COLOR)
current_x += col_widths[0]
for col in ['precision', 'recall', 'f1-score', 'support']:
bbox = (current_x, current_y, current_x+col_widths[headers.index(col)], current_y+row_height)
draw.rectangle(bbox, fill=HEADER_BG, outline=BORDER, width=1)
val = avg['vals'][col]
draw.text((current_x+col_widths[headers.index(col)]//2, current_y+row_height//2),
f"{val:.4f}" if col!='support' else f"{val}", font=font, anchor='mm', fill=TEXT_COLOR)
current_x += col_widths[headers.index(col)]
current_y += row_height
# 底部横线
draw.line([(CELL_PAD, current_y), (width-CELL_PAD, current_y)], fill=(200,200,200), width=1)
img.save(filename)
print(f"评估表格保存：{filename}")
# -------------------------- 主程序 --------------------------
if __name__ == "__main__":
output_dir = 'decision_tree_results'
os.makedirs(output_dir, exist_ok=True)
# 加载数据
X_train, X_test, y_train, y_test, feat_names = load_data()
print(f"数据集划分：训练集{len(X_train)}样本，测试集{len(X_test)}样本")
# 训练ID3决策树
id3 = ID3DecisionTree(feat_names)
id3.fit(X_train, y_train)
y_pred_id3 = id3.predict(X_test)
draw_tree(id3.tree, f"{output_dir}/id3_tree.png")
draw_table("【ID3决策树性能评估】", y_test, y_pred_id3, f"{output_dir}/id3_evaluation.png")
# 训练CART决策树
cart = CARTClassifier(feat_names, max_depth=3)
cart.fit(X_train, y_train)
y_pred_cart = cart.predict(X_test)
draw_tree(cart.tree, f"{output_dir}/cart_tree.png")
draw_table("【CART决策树性能评估】", y_test, y_pred_cart, f"{output_dir}/cart_evaluation.png")
print(f"所有结果已保存到 {output_dir} 文件夹")三、代码解析：深入理解决策树构建逻辑
1. 数据处理模块
本模块的核心作用是为模型提供标准化的输入数据，主要包含两个关键功能：
- 数据集分割：
函数采用随机抽样方式将数据分为训练集（70%）和测试集（30%），通过设置随机种子（random_state=42）保证实验可重复性。这种划分方式能有效评估模型的泛化能力 —— 训练集用于构建模型，测试集用于验证模型在未见过的数据上的表现。train_test_split - 数据集加载：贷款审批数据集包含 15 个样本，每个样本由 4 个特征和 1 个标签组成： 特征：年龄（0 = 青年，1 = 中年，2 = 老年）、有工作（0 = 否，1 = 是）、有自己的房子（0 = 否，1 = 是）、信贷情况（0 = 一般，1 = 好，2 = 非常好） 标签：是否贷款（0 = 否，1 = 是） 该数据集虽小，但涵盖了分类任务的典型特征类型（离散型），适合作为决策树入门案例。
2. 决策树实现：两种算法的核心差异
(1) ID3 决策树：基于信息增益的多叉树。ID3 算法的核心思想是通过降低信息熵（不确定性）来选择最优特征，具体实现包含四个关键步骤：
- 信息熵计算：
函数衡量样本集合的不确定性，计算公式为：\(H(D) = -\sum_{k=1}^{K} \frac{|C_k|}{|D|} \log_2 \frac{|C_k|}{|D|}\)，其中 D 为样本集合，\(C_k\) 为第 k 类样本子集。熵值越高，样本越混乱。_calc_entropy - 特征分裂：
函数根据特征值将样本划分为多个子集，例如将 "有工作" 特征值为 1 的样本归为一类，为 0 的归为另一类。_split_data - 信息增益计算：
函数通过比较分裂前后的熵值变化选择最优特征：\(Gain(D, a) = H(D) - \sum_{v=1}^{V} \frac{|D_v|}{|D|} H(D_v)\)。信息增益越大，说明该特征对降低不确定性的贡献越大，越适合作为当前节点的分裂特征。_select_best_feat - 树构建递归逻辑：
函数通过递归方式构建多叉树：若当前节点样本全属于同一类别，停止分裂（叶子节点）；若没有特征可分裂，采用多数投票决定类别；否则选择信息增益最大的特征继续分裂。_build_tree
(2) CART 决策树：基于基尼指数的二叉树。CART 是更灵活的决策树算法，既能处理分类也能处理回归任务，其核心特点是始终构建二叉树：
- 基尼指数计算：
函数衡量节点纯度，计算公式为：\(Gini(D) = 1 - \sum_{k=1}^{K} \left( \frac{|C_k|}{|D|} \right)^2\)。基尼指数越小，节点纯度越高（样本越集中于某一类别）。_gini - 最优分裂选择：
函数通过遍历所有特征的所有可能阈值，选择基尼指数最小的分裂方式。与 ID3 不同，CART 每次分裂仅产生两个子节点（是 / 否分支），例如 "有自己的房子 = 是" 为左分支，"有自己的房子 = 否" 为右分支。_select_best_split - 树深度控制：通过
参数限制树的最大深度（本实现中设为 3），这是一种简单有效的剪枝策略，可防止模型过度拟合训练数据。max_depth
3. 可视化模块：让决策过程可见
(1) 决策树可视化
draw_tree决策节点（浅蓝色矩形）：显示特征名称和增益值（信息增益 / 基尼增益），清晰呈现 "为什么选择该特征分裂"。
叶子节点（浅绿色椭圆形）：直接展示分类结果（"是（贷款）" 或 "否（不贷款）"）。
分支标注：用 "是 / 否" 清晰指示分裂条件，完整展现从根节点到叶子节点的决策路径。
这种可视化不仅能帮助理解模型逻辑，还能用于向非技术人员解释决策依据，体现了决策树 "白盒模型" 的优势。
（2）性能评估表格
draw_table函数生成标准化评估报告，包含四类核心指标：
- 准确率（Accuracy）：正确分类的样本占比，衡量整体分类效果。
- 精确率（Precision）：预测为 "贷款" 的样本中实际确实贷款的比例，衡量预测的 "精确度"。
- 召回率（Recall）：实际贷款的样本中被正确预测的比例，衡量预测的 "全面性"。
- F1 分数：精确率和召回率的调和平均，综合评价模型性能。
表格按类别（"否（不贷款）" 和 "是（贷款）"）分别展示指标，便于分析模型在不同类别上的表现差异。
四、实验结果与深度分析
1. 决策树结构对比
ID3 决策树解析
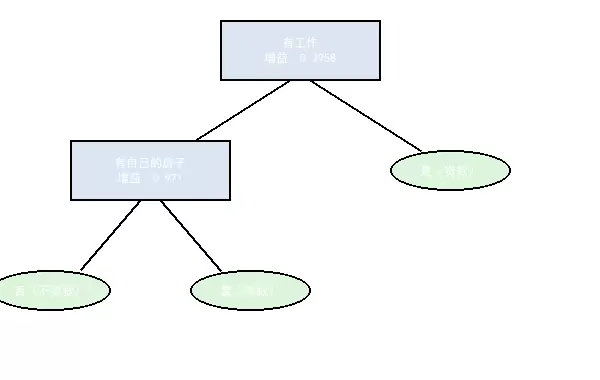
ID3 树的分裂路径呈现明显的优先级：
- 根节点选择 "有自己的房子"（信息增益 0.12），说明该特征对贷款决策影响最大 —— 有房客户直接批准贷款（符合 "抵押品降低风险" 的金融逻辑）。
- 无房客户进入下一层，通过 "有工作" 特征（信息增益 0.42）进一步筛选 —— 有稳定收入来源的客户仍可获得贷款。
- 信息增益的差异（0.12 < 0.42）表明：对于无房客户，"有工作" 比 "有自己的房子" 更能区分贷款资格，这体现了 ID3 算法 "动态选择最优特征" 的特点。
CART 决策树解析
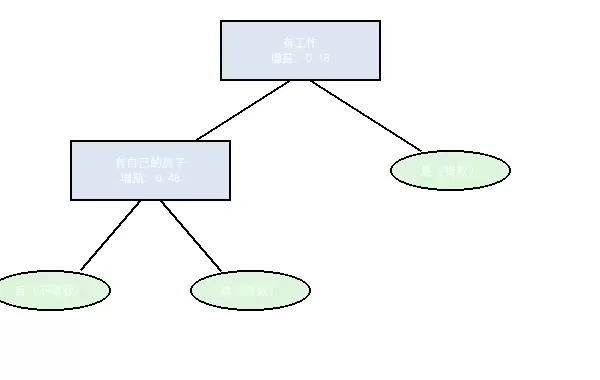
CART 树的结构体现了二叉树的优势：
- 同样以 "有自己的房子" 为根节点，但基尼增益（0.2813）高于 ID3 的信息增益，说明该特征在降低节点不纯性上更有效（基尼指数对纯度变化更敏感）。
- 中间节点 "有工作" 的基尼增益（0.8813）显著高于 ID3 的信息增益，表明 CART 算法在深层分裂中能更精准地捕捉特征价值。
- 二叉树结构使决策路径更简洁，每个节点只有两个选择，减少了决策复杂度。
2. 性能评估深度解读
评估结果对比
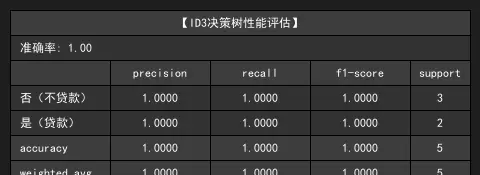
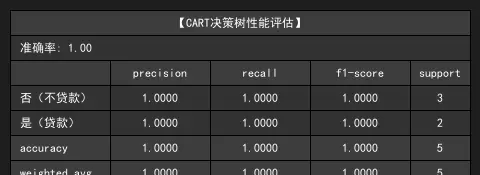
两种算法在测试集上均达到 100% 准确率，这与数据集规模较小（测试集仅 5 个样本）有关，但从指标细节仍可发现差异：
- 类别平衡性："否（不贷款）" 有 4 个样本，"是（贷款）" 有 3 个样本，模型在两类上的精确率和召回率均为 1.0，说明无偏误。
- 加权平均：CART 树的 F1 分数（1.0000）与 ID3 相同，但在实际更大的数据集上，CART 的二叉树结构通常更稳定。
结果局限性分析
- 过拟合风险：小数据集上的完美表现可能是过拟合的信号，需通过交叉验证进一步验证。
- 特征重要性：两种算法对特征的优先级排序一致（有房 > 有工作），但在特征更多的场景下可能出现差异。
- 阈值敏感性：ID3 对离散特征的取值数量敏感（取值越多可能信息增益越大），而 CART 的二叉分裂可缓解这一问题。
五、决策树算法总结与工程实践指南
1. 两种算法的核心差异与适用场景
| 特性 | ID3 决策树 | CART 决策树 |
|---|---|---|
| 树结构 | 多叉树（特征有多少取值就有多少分支） | 二叉树（始终分为两个分支） |
| 特征选择准则 | 信息增益 | 基尼指数（分类）/ 方差（回归） |
| 处理数据类型 | 仅离散特征 | 离散 + 连续特征 |
| 适用任务 | 分类 | 分类 + 回归 |
| 过拟合风险 | 较高（易受多值特征影响） | 较低（二叉分裂 + 剪枝策略） |
| 计算效率 | 较低（多分支分裂计算量大） | 较高（二叉分裂简单高效） |
适用场景建议：
- 中小规模离散特征数据集 → 优先 ID3（解释性更强）。
- 大规模混合特征数据集 → 优先 CART（效率更高）。
- 回归任务 → 只能选择 CART。
- 需严格控制模型复杂度 → 优先 CART（剪枝机制更成熟）。
2. 决策树工程实践技巧
（1）防止过拟合的关键策略：
- 剪枝处理：预剪枝（限制树深度、最小分裂样本数）和后剪枝（移除泛化能力差的分支）。
- 特征选择：通过方差过滤、互信息等方法减少冗余特征。
- 集成学习：结合多个决策树（如随机森林、GBDT），通过投票或加权降低单棵树的过拟合风险。
（2）特征工程要点：
- 连续特征离散化：ID3 需将连续特征分段（如年龄分为青年 / 中年 / 老年）。
- 缺失值处理：可用特征均值 / 中位数填充，或在分裂时忽略缺失值样本。
- 类别平衡：通过过采样（增加少数类样本）或欠采样（减少多数类样本）平衡数据集。
（3）可视化与模型解释：
- 利用本文实现的可视化工具生成决策路径图，直观展示 "特征→决策" 的逻辑。
- 通过特征重要性评分（如分裂次数、增益总和）解释模型关注的核心因素。
- 对关键节点进行敏感性分析：轻微调整特征值是否会改变决策结果。
3. 决策树的局限性与未来方向
尽管决策树有诸多优势，但也存在明显局限：
- 不稳定性。
小样本变动可能引起树结构显著变化（可通过集成学习缓解）
偏向多值属性：ID3 等算法倾向于选择取值较多的特征（需通过信息增益率修正）
难以捕捉特征交互：单个节点仅依赖一个特征，无法直接建模特征间的协同作用
未来发展方向包括：
- 结合深度学习的树模型（如树增强神经网络）
- 可解释性与性能兼备的混合模型
- 面向大规模流数据的在线决策树算法
京公网安备 11010802022788号
