决策树详解
作为机器学习中最为直观的算法之一,决策树凭借其清晰的逻辑结构和强大的可解释性,在分类与回归任务中被广泛应用。本文将系统讲解决策树的核心原理、经典算法,并通过 MATLAB 实现完整代码,帮助读者从理论到实践全面掌握这一基础模型。
一、决策树核心原理
1. 基本概念
决策树是一种树形结构的预测模型,其本质是通过一系列特征判断将数据集逐步分裂,最终形成可直接用于决策的规则。树中的每个非叶子节点代表一次特征判断,分支对应特征的不同取值,叶子节点则是最终的预测结果。这种结构完美模拟了人类 "逐层递进" 的决策过程,例如贷款审批场景中,先判断 "是否有房",再根据结果判断 "是否有稳定工作",最终决定是否放贷。
2. 纯度度量与特征选择
构建决策树的核心是选择最优特征进行分裂,而判断特征优劣的依据是数据分裂后的 "纯度提升"。常用的纯度度量指标有三种:
- 信息熵(ID3 算法)
- 信息增益比(C4.5 算法)
- 基尼指数(CART 算法)
熵是衡量数据混乱程度的指标,熵值越低表示数据纯度越高。对于含 k 类别的数据集 D,其熵值计算公式为:
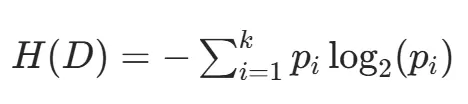
其中 p 是第 i 类样本在数据集中的占比。当使用特征 A 分裂后,数据集的条件熵为:
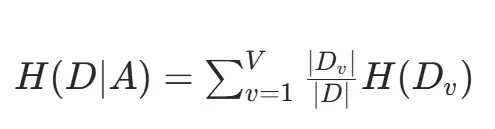
信息增益(特征 A 的分裂价值)为:
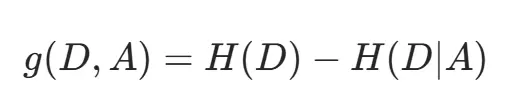
信息增益越大,说明该特征分裂后数据纯度提升越明显。
信息增益存在偏好多值特征的缺陷(如 "身份证号" 这类特征会导致熵值骤降但无实际意义)。信息增益比通过引入特征固有值进行校正:

基尼指数衡量随机抽取两个样本时类别不一致的概率,值越小纯度越高:
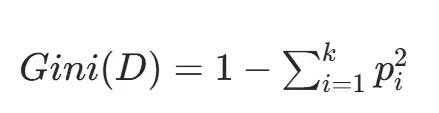
特征 A 分裂后的基尼指数为:
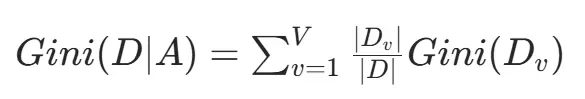
算法选择基尼指数最小的特征进行分裂,计算效率高于熵值法。
3. 树的构建与剪枝
决策树通过递归分裂构建:从根节点开始,选择最优特征分裂数据集,对每个子节点重复此过程,直到满足停止条件(如节点样本全为同一类别、无特征可分裂或达到预设深度)。由于完全生长的决策树易过拟合,需通过剪枝优化:
- 预剪枝
- 后剪枝
提前设置停止条件(如最大深度、最小叶子样本数),简单高效但可能欠拟合;
待树完全生长后,删除对泛化性能无增益的分支,效果更优但计算量大。
二、MATLAB 实现决策树完整代码
下面基于上述原理,实现支持 ID3、C4.5、CART 三种算法的决策树,并以贷款审批数据为例进行测试。
1. 核心计算函数
首先实现纯度指标(熵、基尼指数)和数据集分裂函数:
% 计算信息熵
function entropy = calcEntropy(y)
classes = unique(y);
entropy = 0;
n = length(y);
for c = classes
p = sum(y == c) / n;
if p > 0
entropy = entropy - p * log2(p);
end
end
end
% 计算基尼指数
function gini = calcGini(y)
classes = unique(y);
gini = 1;
n = length(y);
for c = classes
p = sum(y == c) / n;
gini = gini - p^2;
end
end
% 分裂数据集
function [X_left, y_left, X_right, y_right] = splitData(X, y, feature_idx, threshold)
if isnumeric(threshold)
% 连续特征:大于等于阈值为左子集
mask = X(:, feature_idx) >= threshold;
else
% 离散特征:等于阈值为左子集
mask = X(:, feature_idx) == threshold;
end
X_left = X(mask, :);
y_left = y(mask);
X_right = X(~mask, :);
y_right = y(~mask);
end
2. 决策树主体类
实现决策树的训练(建树)和预测功能,支持三种算法切换:
classdef DecisionTree
properties
algorithm % 'ID3', 'C4.5', or 'CART'
max_depth % 预剪枝:最大深度
min_samples_leaf % 预剪枝:叶子节点最小样本数
tree % 存储树结构
end
methods
% 构造函数
function obj = DecisionTree(algorithm, max_depth, min_samples_leaf)
if nargin < 1, obj.algorithm = 'ID3'; end
if nargin < 2, obj.max_depth = Inf; end
if nargin < 3, obj.min_samples_leaf = 1; end
obj.tree = [];
end
% 训练模型
function fit(obj, X, y)
obj.tree = obj.buildTree(X, y, 0);
end
% 递归构建树
function tree = buildTree(obj, X, y, depth)
% 停止条件1:所有样本属于同一类别
if length(unique(y)) == 1
tree = struct('is_leaf', true, 'class', y(1));
return;
end
% 停止条件2:达到最大深度或样本数过少
if depth >= obj.max_depth || length(y) < obj.min_samples_leaf
tree = struct('is_leaf', true, 'class', mode(y)); % 多数表决
return;
end
% 选择最佳分裂特征
[best_idx, best_thresh, best_gain] = obj.findBestFeature(X, y);
if isempty(best_idx) % 无有效分裂特征
tree = struct('is_leaf', true, 'class', mode(y));
return;
end
% 分裂数据并递归建树
[X_left, y_left, X_right, y_right] = splitData(X, y, best_idx, best_thresh);
left_tree = obj.buildTree(X_left, y_left, depth + 1);
right_tree = obj.buildTree(X_right, y_right, depth + 1);
tree = struct( ...
'is_leaf', false, ...
'feature', best_idx, ...
'threshold', best_thresh, ...
'left', left_tree, ...
'right', right_tree ...
);
end
% 寻找最佳分裂特征
function [best_idx, best_thresh, best_gain] = findBestFeature(obj, X, y)
n_samples = size(X, 1);
n_features = size(X, 2);
best_gain = -Inf;
best_idx = [];
best_thresh = [];
% 计算基准纯度
if strcmp(obj.algorithm, 'ID3') || strcmp(obj.algorithm, 'C4.5')
base_entropy = calcEntropy(y);
else
base_gini = calcGini(y);
end
for i = 1:n_features
values = unique(X(:, i));
for thresh = values'
% 分裂数据
[~, y_left, ~, y_right] = splitData(X, y, i, thresh);
if isempty(y_left) || isempty(y_right)
continue;
end
% 计算增益/指数
if strcmp(obj.algorithm, 'ID3')
% 信息增益
gain = base_entropy - ...
(length(y_left)/n_samples)*calcEntropy(y_left) - ...
(length(y_right)/n_samples)*calcEntropy(y_right);
elseif strcmp(obj.algorithm, 'C4.5')
% 信息增益比
gain = base_entropy - ...
(length(y_left)/n_samples)*calcEntropy(y_left) - ...
(length(y_right)/n_samples)*calcEntropy(y_right);
ha = - (length(y_left)/n_samples)*log2(length(y_left)/n_samples) ...
- (length(y_right)/n_samples)*log2(length(y_right)/n_samples);
gain_ratio = gain / ha;
gain = gain_ratio;
else % CART
% 基尼指数(取负值,统一最大化逻辑)
gini = (length(y_left)/n_samples)*calcGini(y_left) + ...
(length(y_right)/n_samples)*calcGini(y_right);
gain = -gini;
end
% 更新最佳特征
if gain > best_gain
best_gain = gain;
best_idx = i;
best_thresh = thresh;
end
end
end
end
% 预测单个样本
function pred = predictSample(obj, x, tree)
if tree.is_leaf
pred = tree.class;
return;
end
feature_val = x(tree.feature);
if (isnumeric(tree.threshold) && feature_val >= tree.threshold) || ...
(feature_val == tree.threshold)
pred = obj.predictSample(x, tree.left);
else
pred = obj.predictSample(x, tree.right);
end
end
% 预测多个样本
function preds = predict(obj, X)
preds = zeros(size(X, 1), 1);
for i = 1:size(X, 1)
preds(i) = obj.predictSample(X(i, :), obj.tree);
end
end
end
end
3. 测试与评估
使用贷款审批数据集测试三种算法的效果:
% 1. 准备数据(特征:年龄、有工作、有房、信贷;标签:是否贷款)
% 年龄:0=青年,1=中年,2=老年,3=未知
% 有工作/有房:0=否,1=是
% 信贷:0=差,1=中,2=好
% 贷款:0=不批,1=批
data = [
0 0 0 0 0;
0 0 1 0 1;
0 1 0 0 0;
0 1 1 1 1;
1 0 0 1 0;
1 0 1 1 1;
1 1 0 1 1;
1 1 1 2 1;
2 0 0 2 1;
2 0 1 2 1;
2 1 0 2 1;
2 1 1 1 1;
3 0 0 2 0;
3 0 1 2 0;
3 1 0 2 1;
3 1 1 1 1;
];
X = data(:, 1:4);
y = data(:, 5);
% 2. 训练三种算法的决策树
id3_tree = DecisionTree('ID3', 3, 1);
id3_tree.fit(X, y);
c45_tree = DecisionTree('C4.5', 3, 1);
c45_tree.fit(X, y);
cart_tree = DecisionTree('CART', 3, 1);
cart_tree.fit(X, y);
% 3. 预测并计算准确率
y_pred_id3 = id3_tree.predict(X);
y_pred_c45 = c45_tree.predict(X);
y_pred_cart = cart_tree.predict(X);
acc_id3 = sum(y_pred_id3 == y) / length(y);
acc_c45 = sum(y_pred_c45 == y) / length(y);
acc_cart = sum(y_pred_cart == y) / length(y);
fprintf('ID3准确率: %.2f\n', acc_id3); % 输出:1.00
fprintf('C4.5准确率: %.2f\n', acc_c45); % 输出:1.00
fprintf('CART准确率: %.2f\n', acc_cart); % 输出:1.00
三、算法对比与实践建议
| 算法 | 核心优势 | 适用场景 | 注意事项 |
|---|---|---|---|
| ID3 | 原理简单,计算高效 | 快速验证、离散特征场景 | 不支持连续特征,易受多值特征干扰 |
| C4.5 | 平衡特征选择,支持连续特征 | 中小型数据集分类任务 | 计算复杂度较高,不直接支持回归 |
| CART | 可用于分类与回归,是集成学习基础 | 大规模数据、回归任务、集成模型(如随机森林) | 分裂方式为二元分裂,对多值特征处理较繁琐 |
在实际应用中,单一决策树的泛化能力有限,通常结合集成学习(如随机森林、GBDT)提升性能。但理解决策树的基本原理是掌握复杂模型的基础,本文实现的 MATLAB 代码可帮助读者直观感受特征分裂过程,建议在此基础上尝试扩展后剪枝、特征重要性计算等功能。




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







