一文读懂决策树：原理、实战与应用场景

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

在机器学习领域，决策树是一种既简洁明了又功能强大的算法，无论是分类任务还是回归任务都能应对。其主要优点在于具有高度的可解释性 —— 最终生成的模型就像一棵 “判断树”，每个分支代表一个决策规则，即使是非专业人员也能轻松理解模型的逻辑。本文将从原理到实践，带领大家全面掌握决策树算法，特别适合初学者入门和工程师实际应用。

一、决策树的核心概念：通过“树结构”理解决策逻辑

决策树的构造与现实中的 “树” 高度相似，主要包括三个核心部分：

• 根节点：代表整个数据集，是决策树的起点，需要通过特征判断进行首次分裂；
• 内部节点：每个内部节点对应一个 “特征判断条件”（例如 “年龄是否超过 30 岁”“收入是否高于 50 万”），节点分裂后生成多个分支；
• 叶节点：决策树的终点，每个叶节点对应一个 “预测结果”（分类任务中是类别，回归任务中是具体数值）。

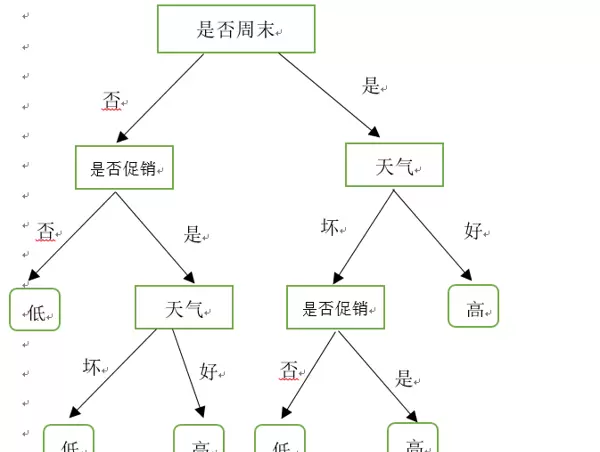
举个生活中的例子：我们判断 “是否购买一件衣服” 的决策过程，就可以转换为一棵决策树：

• 根节点：待决策的数据集（所有考虑购买的衣服）；
• 内部节点 1：“价格是否低于 500 元？”（是→分支 1，否→分支 2）；
• 内部节点 2（分支 1 下）：“款式是否为通勤风？”（是→分支 1-1，否→分支 1-2）；
• 叶节点 1-1：“购买”，叶节点 1-2：“不购买”，叶节点 2：“不购买”。

这种 “if-else” 的判断逻辑，正是决策树的本质 —— 通过对特征的逐步分解，将复杂的决策问题简化为一系列简单的小问题。

二、决策树的关键原理：如何“合理”分裂节点？

决策树的核心挑战在于：

• 每次分裂节点时，如何选择最优的特征和判断条件？如果选择不当，会导致树的深度过大、过拟合（仅适应训练数据，不适应新数据）等问题。

目前主流的节点分裂准则有三种，分别对应不同的决策树算法：

1. 信息增益（ID3 算法）

   核心思想：用 “信息熵” 衡量数据的混乱程度（熵越高，数据越混杂），通过分裂节点降低数据的熵，降低的程度就是 “信息增益”。选择信息增益最大的特征进行分裂。

   公式：
   信息熵 \(H(D) = -\sum_{k=1}^{K} \frac{|C_k|}{|D|} \log_2 \frac{|C_k|}{|D|}\)（\(D\) 为数据集，\(C_k\) 为 \(D\) 中第 \(k\) 类样本）；
   信息增益 \(Gain(D,a) = H(D) - \sum_{v=1}^{V} \frac{|D_v|}{|D|} H(D_v)\)（\(a\) 为特征，\(D_v\) 为 \(a\) 取第 \(v\) 个值的样本子集）。

   缺点：倾向于选择取值较多的特征（例如 “用户 ID” 这类唯一值特征，分裂后熵会降为 0，但没有泛化能力），容易过拟合。

2. 信息增益比（C4.5 算法）

   核心思想：为了克服 ID3 的缺陷，在信息增益的基础上增加 “特征固有值” 的惩罚项 —— 取值越多的特征，固有值越大，信息增益比会被削弱。

   公式：
   信息增益比 \(Gain\_ratio(D,a) = \frac{Gain(D,a)}{IV(a)}\)，其中 \(IV(a) = -\sum_{v=1}^{V} \frac{|D_v|}{|D|} \log_2 \frac{|D_v|}{|D|}\)（\(IV(a)\) 为特征 \(a\) 的固有值）。

   优势：平衡了特征取值数量的影响，是 ID3 的改进版，更适合实际场景。

3. 基尼系数（CART 算法）

   核心思想：用 “基尼系数” 衡量数据的不纯度（基尼系数越小，数据越纯净），选择基尼系数最小的特征进行分裂。CART 算法是目前应用最广的决策树算法，支持分类和回归任务。

   公式：
   基尼系数 \(Gini(D) = 1 - \sum_{k=1}^{K} \left( \frac{|C_k|}{|D|} \right)^2\)；
   特征 \(a\) 的基尼系数 \(Gini\_index(D,a) = \sum_{v=1}^{V} \frac{|D_v|}{|D|} Gini(D_v)\)。

   优势：计算效率比信息熵更高（无需对数运算），且 CART 树是 “二叉树”（每个节点最多分裂为两个分支），结构更简洁，易于剪枝和并行计算。

三、决策树的“剪枝”：解决过拟合的关键手段

如果不对决策树加以限制，它会一直分裂到所有叶节点的样本都属于同一类别（或回归误差为 0），此时树的深度会非常大，模型会 “死记硬背” 训练数据的特征，导致对新数据的预测准确率大幅下降（过拟合）。

剪枝是解决过拟合的核心方法，分为“预剪枝”和“后剪枝”两种：

1. 预剪枝（Pre-pruning）

   思路：在决策树生成过程中，提前停止节点分裂（“早停”），避免树过度生长。

   常见策略：
   限制树的最大深度（例如max_depth=5，超过此深度的节点不再分裂）；

限制叶节点的最小样本量（例如min_samples_leaf=10，样本少于 10 的叶节点不会分裂）；

限定节点分裂所需的最少样本数（例如min_samples_split=20，样本不足 20 的节点不进行分裂）；

设定最大特征数量（例如max_features=10，每次分割仅从 10 个特征中选择最优者）。

优点：计算效率较高，能防止不必要的分割；缺点：可能“欠拟合”（树的深度不足，未能学习足够的特性）。

2. 后剪枝（Post-pruning）

思路：先允许决策树自由生长至完全状态，然后从叶节点向根节点反向回溯，移除对模型表现没有贡献的分支。

核心原则：利用“验证集”评估分支的有效性 —— 如果去除某个分支后，模型在验证集上的准确度未下降（甚至提高），则可删除该分支。

优点：剪枝更为精确，过拟合的风险更低；缺点：计算开销大（需要先生成完整的树，再进行回溯修剪）。

在实际运用中，由于效率高、实现简便，预剪枝成为了更常见的选择（例如 sklearn 中的DecisionTreeClassifier默认支持预剪枝参数）。

四、Python 实战：用决策树完成鸢尾花分类

接下来，我们将使用sklearn库执行一个经典的分类任务——预测鸢尾花种类，以帮助大家直观理解决策树的应用流程。

1. 环境准备

首先确保已安装必要的库（若未安装，请运行以下命令）：

pip install sklearn pandas numpy matplotlib

2. 完整代码与步骤解析

步骤 1：导入库并加载数据

# 导入核心库

from sklearn.datasets import load_iris

from sklearn.tree import DecisionTreeClassifier, plot_tree

from sklearn.model_selection import train_test_split

from sklearn.metrics import accuracy_score, classification_report

import matplotlib.pyplot as plt

import pandas as pd

# 加载鸢尾花数据集（sklearn内置数据集）

iris = load_iris()

X = iris.data # 特征（花萼长度、花萼宽度、花瓣长度、花瓣宽度）

y = iris.target # 标签（0=山鸢尾，1=变色鸢尾，2=维吉尼亚鸢尾）

feature_names = iris.feature_names # 特征名称

target_names = iris.target_names # 标签名称

# 查看数据基本信息

print("数据集形状：", X.shape) # 输出 (150, 4)，150个样本，4个特征

print("特征名称：", feature_names)

print("标签名称：", target_names)

步骤 2：划分训练集和测试集

将数据按照 7:3 的比例分为训练集（用于模型训练）与测试集（用于评估模型性能）：

X_train, X_test, y_train, y_test = train_test_split(

X, y, test_size=0.3, random_state=42 # test_size=0.3表示30%为测试集，random_state固定随机种子

)

print("训练集样本数：", X_train.shape[0]) # 105个样本

print("测试集样本数：", X_test.shape[0]) # 45个样本

步骤 3：训练决策树模型

采用 CART 算法（默认设置）构建决策树，并设定预剪枝参数（例如最大深度设为 3，以防止过拟合）：

# 初始化决策树分类器

dt_model = DecisionTreeClassifier(

max_depth=3, # 预剪枝：限制树的最大深度为3

min_samples_leaf=5, # 预剪枝：叶节点最小样本数为5

random_state=42

)

# 训练模型

dt_model.fit(X_train, y_train)

print("决策树训练完成！")

步骤 4：模型预测与性能评估

使用训练完成的模型对测试集进行预测，并计算准确率、生成分类报告：

# 测试集预测

y_pred = dt_model.predict(X_test)

# 计算准确率（预测正确的样本数/总样本数）

accuracy = accuracy_score(y_test, y_pred)

print(f"\n模型测试集准确率：{accuracy:.2f}") # 通常准确率会在95%以上

# 生成详细分类报告（包含精确率、召回率、F1分数）

print("\n分类报告：")

print(classification_report(y_test, y_pred, target_names=target_names))

步骤 5：可视化决策树

通过plot_tree函数展示决策树的结构，直观查看模型的决策逻辑：

# 设置画布大小

plt.figure(figsize=(12, 8))

# 绘制决策树

plot_tree(

dt_model,

feature_names=feature_names, # 显示特征名称

class_names=target_names, # 显示类别名称

filled=True, # 用颜色填充节点（颜色越深，类别越纯净）

rounded=True, # 节点边角圆润

fontsize=10

)

# 保存图片（可选）

plt.savefig("iris_decision_tree.png", dpi=300, bbox_inches="tight")

plt.show()

3. 结果解读

准确率：通常可达到 95% 以上，表明决策树在鸢尾花分类任务上表现良好；

分类报告：精确率（Precision）、召回率（Recall）和 F1 分数均接近 1，显示模型对三种鸢尾花的预测都非常准确；

可视化图：每个节点会标注“特征判断条件”（例如“花瓣宽度 (cm) ≤ 0.8”）、“基尼系数”（Gini）、“样本数量”（samples）、“类别分布”（value）以及“预测类别”（class），清晰展现了模型的决策过程。

五、决策树的优劣与适用场景

1. 优点

具有很强的可解释性：模型结构直观，能够明了地输出决策规则（如“如果花瓣宽度≤0.8cm，则预测为山鸢尾”），适合医疗、金融等需要高可解释性的场合；

无需特征预处理：对特征尺度不敏感（不需要归一化/标准化），能容忍一定程度的缺失值和异常值；

训练效率较高：时间复杂度低（与样本数量、特征数量成线性关系），适合中小型数据集；

支持多任务处理：不仅能进行分类（输出类别），还能进行回归（输出连续值），也能应对多标签任务。

2. 缺点

容易过拟合：默认情况下会完全生长，对噪声敏感，需通过剪枝或集成学习来优化；

对于不平衡数据的敏感性：如果某类样本在数据中占比极高，模型会偏向于预测该类别，可以通过采样（如过采样/欠采样）平衡数据；

稳定性较差：微小的样本变化可能引起树结构的重大改变（“高方差”），可以采用集成学习方法（如随机森林、XGBoost）来改善。

3. 典型应用场景

金融风控：评估用户是否存在违约风险（例如，“收入> 50 万且信用良好→低风险”）；

医疗诊断：辅助判断患者是否患病（如“体温> 38.5℃且咳嗽→疑似流感”）；

客户分层

对用户进行划分（例如 “消费频率 > 10 次且平均花费 > 200 元→高价值客户”）；

工业质检：评估产品是否合格（例如 “尺寸偏差≤0.1mm 且重量≥500g→合格”）。

六、总结与拓展

决策树是机器学习中的“初级但有效”的算法，其核心在于通过“节点分裂 - 剪枝”的过程，建立直观、易于理解的决策模型。本文从理论（分裂标准、剪枝）、实践（鸢尾花分类）、应用（场景及优缺点）三个方面进行探讨，旨在帮助大家掌握决策树的主要逻辑。

如果希望进一步提高模型性能，可以考虑以下方法：

• 集成算法
• 随机森林：通过多棵决策树投票减少方差，解决过拟合问题；
• XGBoost/LightGBM：利用梯度提升（Gradient Boosting）进一步提高精度，是工业界处理分类 / 回归任务的“高效工具”。

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：决策树 classifier Matplotlib Selection PRECISION

相关内容：决策树原理应用