发帖
雷达卡
题目
给定一个二叉树，目标是找出它的最小深度。
最小深度定义为从根节点到最近叶子节点的最短路径上的节点数量。
说明：叶子节点是指没有任何子节点的节点。
示例 1：
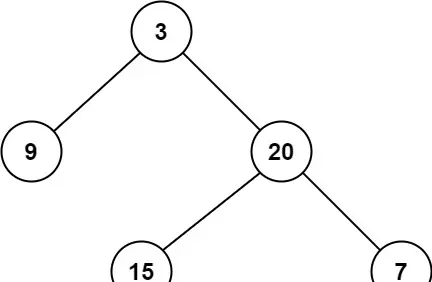
输入：root = [3,9,20,null,null,15,7]
输出：2
示例 2：
输入：root = [2,null,3,null,4,null,5,null,6]
输出：5
解析
面对这个问题，我们可能会首先想到利用求解二叉树最大深度的方法：
return Math.max(lDepth + rDepth) + 1;然而，尝试直接替换为求最小深度的代码：
return Math.min(lDepth + rDepth) + 1;很快就会发现这种方法行不通，因为最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
当某一侧的子树为空时，上述方法会错误地返回1（仅计算根节点），但实际的最小深度应该是到另一侧非空子树的最近叶子节点的节点数量。
总结
对于最大深度的问题，可以直接选取左右子树深度中的较大值，因为即使存在空子树也不会影响最长路径的计算。
但对于最小深度的问题，则不能简单地选取左右子树深度中的较小值，因为需要排除空子树的影响，确保路径最终到达的是真正的叶子节点。
因此，解决最小深度问题时，需要特别处理空子树的情况，而最大深度问题则无需如此。
具体来说：
- 叶子节点的定义是左右子节点均为 null 的节点。
- 若根节点的左右子节点均为空，则返回1。
- 若根节点的一个子节点为空，则返回另一个非空子节点的深度。
- 若根节点的左右子节点均不为空，则返回两者中较小深度的节点值。
代码可以通过简化处理，当左右子节点均为空时，lDepth 和 rDepth 均为0，可以与只有一个子节点为空的情况合并，即返回 lDepth + rDepth + 1。
答案
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var minDepth = function(root) {
if(root === null) return 0;
const lDepth = minDepth(root.left);
const rDepth = minDepth(root.right);
//1.如果左孩子和右孩子有为空的情况，直接返回lDepth + rDepth + 1
//2.如果都不为空，返回较小深度+1
if(root.left !== null && root.right !== null) {
return Math.min(lDepth, rDepth) + 1;
} else {
return lDepth + rDepth + 1;
}
};复杂度分析
时间复杂度：O(n)
空间复杂度：O(n)
京公网安备 11010802022788号
