五相永磁同步电机的数学模型与矢量控制研究
在电机控制技术中,五相永磁同步电机(PMSM)因其独特的优势而日益受到重视。为了实现对其的有效控制,构建精确的数学模型及合理的矢量控制策略至关重要。在此过程中,MATLAB 成为了强大的工具。
构建旋转坐标系下的数学模型
五相 PMSM 矢量控制的基础在于创建旋转坐标系下的电机数学模型。这一步骤中,选择正确的派克变换矩阵尤为关键。通过应用派克变换,可以将电机在固定坐标系中的复杂模型转化为旋转坐标系中的简化模型,便于进一步的分析与控制。
假设五相 PMSM 的定子电压方程在固定坐标系下表示如下:
\[ \begin{bmatrix} u_{a} \\ u_{b} \\ u_{c} \\ u_{d} \\ u_{e} \end{bmatrix} = \begin{bmatrix} R & 0 & 0 & 0 & 0 \\ 0 & R & 0 & 0 & 0 \\ 0 & 0 & R & 0 & 0 \\ 0 & 0 & 0 & R & 0 \\ 0 & 0 & 0 & 0 & R \end{bmatrix} \begin{bmatrix} i_{a} \\ i_{b} \\ i_{c} \\ i_{d} \\ i_{e} \end{bmatrix} + p \begin{bmatrix} \psi_{a} \\ \psi_{b} \\ \psi_{c} \\ \psi_{d} \\ \psi_{e} \end{bmatrix} \]
其中,\( u \) 表示相电压,\( i \) 表示相电流,\( R \) 代表定子电阻,\( p \) 是微分运算符,\( \psi \) 表示磁链。
通过派克变换,将上述模型转换至旋转坐标系 \( d - q \) 中,数学模型会相应地发生变化。对于五相系统,派克变换矩阵 \( T \) 可以表示为:
\[ T = \begin{bmatrix} \cos(\theta) & \cos(\theta - \frac{2\pi}{5}) & \cos(\theta - \frac{4\pi}{5}) & \cos(\theta + \frac{2\pi}{5}) & \cos(\theta + \frac{4\pi}{5}) \\ -\sin(\theta) & -\sin(\theta - \frac{2\pi}{5}) & -\sin(\theta - \frac{4\pi}{5}) & -\sin(\theta + \frac{2\pi}{5}) & -\sin(\theta + \frac{4\pi}{5}) \\ \cos(2\theta) & \cos(2(\theta - \frac{2\pi}{5})) & \cos(2(\theta - \frac{4\pi}{5})) & \cos(2(\theta + \frac{2\pi}{5})) & \cos(2(\theta + \frac{4\pi}{5})) \\ -\sin(2\theta) & -\sin(2(\theta - \frac{2\pi}{5})) & -\sin(2(\theta - \frac{4\pi}{5})) & -\sin(2(\theta + \frac{2\pi}{5})) & -\sin(2(\theta + \frac{4\pi}{5})) \\ \frac{1}{\sqrt{5}} & \frac{1}{\sqrt{5}} & \frac{1}{\sqrt{5}} & \frac{1}{\sqrt{5}} & \frac{1}{\sqrt{5}} \end{bmatrix} \]
使用该变换矩阵,可以将固定坐标系下的方程转换到旋转坐标系 \( d - q \) 中,从而获得新的电压、电流和磁链关系,为后续的矢量控制策略提供基础。
基于模型的矢量控制策略
基于前述旋转坐标系下的数学模型,可以设计五相 PMSM 的矢量控制策略。矢量控制的主要目标是对电机的转矩和磁链进行解耦控制,以实现类似于直流电机的控制性能。
利用 MATLAB 的 Simulink 工具,可以构建五相 PMSM 矢量控制系统的仿真模型,进行详细的仿真研究。目前,该程序已经调试完成,可以直接运行。
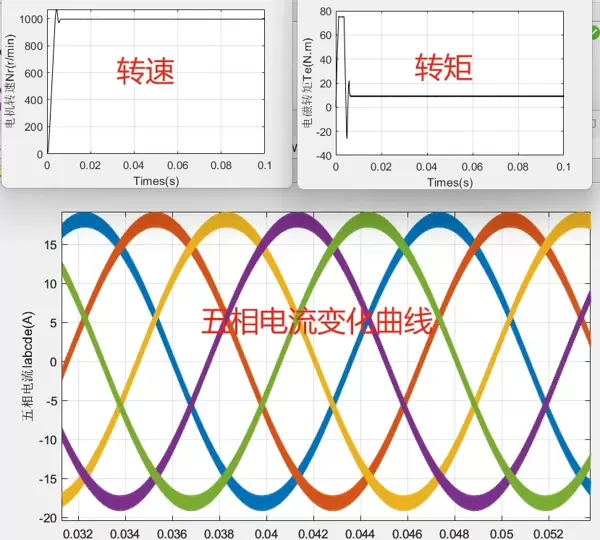
通常,在 \( d - q \) 坐标系中,我们能通过调节 \( i_d \) 和 \( i_q \) 电流分量来分别管理电机的磁场和转矩。为了确保电机在最佳转矩/电流比下工作,从而提升效率,通常设定 \( i_d = 0 \)。
以速度环和电流环组成的双闭环控制系统为例,其中速度环的输出作为电流环的目标输入。对于速度环,可以采用传统的PI控制器,下面给出了一个使用Matlab/Simulink的伪代码示例:
% 速度环PI控制器参数
Kp_speed = 0.5;
Ki_speed = 10;
integral_speed = 0;
prev_error_speed = 0;
% 速度给定和反馈
speed_ref = 1000; % 速度给定值,单位rpm
speed_fb = get_speed_feedback(); % 获取速度反馈值的函数
error_speed = speed_ref - speed_fb;
integral_speed = integral_speed + error_speed * Ts; % Ts为采样时间
i_q_ref = Kp_speed * error_speed + Ki_speed * integral_speed + prev_error_speed;
prev_error_speed = error_speed;在电流环的设计中,同样运用PI控制器来追踪来自速度环输出的 \( i_q_{ref} \) 和 \( i_d_{ref} \)(多数情况下 \( i_d_{ref} = 0 \)),进而产生最终的PWM控制信号,用于驱动逆变器,实现对电机的有效控制。
% 电流环PI控制器参数
Kp_current = 1;
Ki_current = 50;
integral_iq = 0;
prev_error_iq = 0;
% 电流反馈
i_q_fb = get_iq_feedback(); % 获取i_q电流反馈值的函数
error_iq = i_q_ref - i_q_fb;
integral_iq = integral_iq + error_iq * Ts;
u_q = Kp_current * error_iq + Ki_current * integral_iq + prev_error_iq;
prev_error_iq = error_iq;借助MATLAB中的Simulink工具,我们可以便捷地构建五相永磁同步电机(PMSM)矢量控制系统的仿真模型,以此来模拟并测试前面提到的控制策略。在Simulink环境下,通过合理配置电机模型组件、控制单元以及逆变器模块,可以组装出一套完整的仿真系统。
例如,电机模型可以从Simscape Electrical库中选择永磁同步电机模型,并依据实际电机的规格进行参数设定。控制单元部分,则可根据之前提供的代码逻辑来构建速度环和电流环的PI控制器。逆变器模块的作用是将控制器输出的电压信号转化为真实的PWM信号,用于驱动电机。
模型搭建完成后,启动仿真过程,即可实时监控电机的速度、转矩和电流等核心参数的变化,以此检验所设计的数学模型和控制策略的有效性。值得一提的是,本项目中的程序已经调试完毕,可以直接运行,这对于系统性能的评估和改进提供了极大的便利。
通过在Matlab平台上对五相永磁同步电机的数学建模和矢量控制策略的研究与仿真,我们不仅能够更加深刻地了解五相PMSM的工作特性,还能为实际应用中的电机控制提供坚实的理论基础和实践经验。无论是电动汽车还是工业伺服系统,五相PMSM都展现出其独特的优势,有望在未来发挥更为重要的作用。





 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







