【元启发算法】ACO蚁群算法自然协作的数学诗篇

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

目录

• 序章：林间小径的启示
• 问题之源：组合优化的困境
• 算法核心：群体协作的数学之美
• 参数艺术：协作的精细调节
• 实践落地：MATLAB实现与可视化
• 结果解读与技术价值
• 应用场景与扩展思考
• 结语：自然智慧的数学颂歌

序章：林间小径的启示

清晨，森林中的一队蚂蚁开始了它们的食物探寻之旅。起初，每只蚂蚁的行进路线都是随机的，但不久之后，一条从巢穴直达食物的最佳路径奇迹般地显现出来。这些蚂蚁没有全局视角，也没有中央指挥系统，仅通过简单的信息素交流，便找到了最短的路径。

技术如同一座桥梁，使得算法能够学习自然界中的协作智慧。在解决复杂的组合优化问题时，蚁群优化算法（Ant Colony Optimization, ACO）就像是这群聪明的蚂蚁，通过分布式的合作，在巨大的解空间中探索出最佳路径。

问题之源：组合优化的困境

旅行商问题的挑战

设想你是一名旅行商人，需要访问多个城市，且每个城市只能访问一次，最终返回起点。如何规划行程才能使总的旅行距离最短？这便是著名的旅行商问题（Traveling Salesman Problem, TSP）。

随着城市数量的增加，可能的路线数量呈指数级增长：

• 10个城市：大约362万条路线
• 20个城市：约2.43×10^18条路线
• 50个城市：比宇宙中的原子还要多

传统方法面对如此庞大的数据量，几乎无法有效解决问题，而蚁群算法则能从随机搜索开始，逐步逼近优质解决方案。

自然灵感与算法对应

自然现象	算法对应	数学意义
蚂蚁随机探索	初始解生成	全局搜索
信息素分泌	解质量评估	正反馈机制
信息素挥发	遗忘机制	避免早熟收敛
路径选择偏好	概率选择	平衡探索与利用

算法核心：群体协作的数学之美

基本概念解析

每只“人工蚂蚁”在构建解的过程中，通过信息素轨迹和启发式信息来指导搜索：

• 信息素τ：类似于蚂蚁留下的化学信号，表示路径的历史优良程度
• 能见度η：类似于路径的直观吸引力，在TSP中通常取距离的倒数

状态转移规则

蚂蚁k从城市i转移到城市j的概率为：

P_ijk = [τ_ij]^α * [η_ij]^β / ∑_{l∈允许城市} [τ_il]^α * [η_il]^β

用生活中的例子来理解：

• 信息素项：像路标指引，“许多人走过这条路，说明它不错”
• 启发式项：像直觉判断，“那条路看起来更近”
• α、β参数：平衡“信任经验”与“信任直觉”的权重

信息素更新规则

• 局部更新（边走边挥发）：τ_ij = (1 - ρ) * τ_ij + ρ * τ₀
• 全局更新（只更新最优路径）：τ_ij = (1 - ρ) * τ_ij + ρ * Δτ_ij
• Δτ_ij = Q / L_best

挥发机制的意义：就像记忆会随着时间淡忘，避免算法过早陷入局部最优。

参数艺术：协作的精细调节

关键参数的作用

• 信息素重要性α：控制历史经验的影响力
• 启发式重要性β：控制直观启发信息的影响力
• 挥发系数ρ：控制信息素的持久性，平衡新旧信息
• 信息素强度Q：控制每次信息素分泌的量

参数调节的平衡之道

优秀的ACO参数调节如同调配香水，需要在持久性和挥发性之间找到完美的平衡：

• ρ太小：信息素积累过多，容易陷入局部最优
• ρ太大：信息素挥发过快，失去学习能力
• α/β比：决定算法是“经验主义”还是“理性主义”

实践落地：MATLAB实现与可视化

matlab

%% 蚁群优化算法（ACO）MATLAB实现 - 旅行商问题求解
% 功能说明：本代码实现蚁群算法求解旅行商问题（TSP）
% 使用att48数据集（48城市TSP问题）展示算法过程
% 运行后将生成路径演化动画和收敛曲线

clear; close all; clc;

%% 问题初始化 - 生成模拟城市坐标
rng(42); % 设置随机种子保证可重复性
n_cities = 25; % 城市数量

% 生成城市坐标（在单位正方形内随机分布）
cities = rand(n_cities, 2);

% 计算距离矩阵
dist_matrix = zeros(n_cities, n_cities);
for i = 1:n_cities
    for j = 1:n_cities
        dist_matrix(i, j) = norm(cities(i, :) - cities(j, :));
    end
end

%% 蚁群算法参数设置
n_ants = 30;        % 蚂蚁数量
max_iter = 200;     % 最大迭代次数
alpha = 1.0;        % 信息素重要性因子
beta = 2.0;         % 启发式因子重要性
rho = 0.1;          % 信息素挥发系数
Q = 1.0;            % 信息素强度常数
tau0 = 0.1;         % 初始信息素水平

%% 算法初始化
% 初始化信息素矩阵
pheromone = tau0 * ones(n_cities, n_cities);

% 初始化启发式信息矩阵（距离的倒数）
heuristic = 1 ./ (dist_matrix + eye(n_cities));

% 记录最佳解
best_path = [];
best_length = inf;

% 记录收敛过程
convergence_curve = zeros(max_iter, 1);
diversity_curve = zeros(max_iter, 1); % 解多样性记录

%% 创建可视化窗口
figure('Position', [100, 100, 1400, 600]);

%% 蚁群算法主循环
for iter = 1:max_iter
    % 存储所有蚂蚁的路径和路径长度
    ant_paths = zeros(n_ants, n_cities);
    ant_lengths = zeros(n_ants, 1);
    
    %% 每只蚂蚁构建解
    for k = 1:n_ants
        % 初始化蚂蚁的路径和访问标记
        path = zeros(1, n_cities);
        visited = false(1, n_cities);
        
        % 随机选择起点城市
        current_city = randi(n_cities);
        path(1) = current_city;
        visited(current_city) = true;
        
        %% 构建完整路径
        for step = 2:n_cities
            % 计算转移到各个未访问城市的概率
            allowed_cities = find(~visited);
            probabilities = zeros(1, length(allowed_cities));
            
            for idx = 1:length(allowed_cities)
                j = allowed_cities(idx);
                % 计算信息素和启发式因子的乘积
                probabilities(idx) = pheromone(current_city, j)^alpha * ...
                                    heuristic(current_city, j)^beta;
            end
            
            % 概率归一化
            if sum(probabilities) > 0
                probabilities = probabilities / sum(probabilities);
            else
                % 如果所有概率都为0，使用均匀分布
                probabilities = ones(1, length(allowed_cities)) / length(allowed_cities);
            end
            
            % 轮盘赌选择下一个城市
            next_city_idx = roulette_wheel_selection(probabilities);
            next_city = allowed_cities(next_city_idx);
            
            path(step) = next_city;
            visited(next_city) = true;
            current_city = next_city;
        end
        
        % 计算路径长度
        path_length = calculate_path_length(path, dist_matrix);
        
        ant_paths(k, :) = path;
        ant_lengths(k) = path_length;
        
        % 更新全局最优解
        if path_length < best_length
            best_length = path_length;
            best_path = path;
        end
    end
    
    %% 信息素挥发
    pheromone = (1 - rho) * pheromone;
    
    %% 信息素更新（精英策略）
    % 只对最优路径进行信息素增强
    for i = 1:(n_cities-1)
        city_i = best_path(i);
        city_j = best_path(i+1);
        pheromone(city_i, city_j) = pheromone(city_i, city_j) + Q / best_length;
        pheromone(city_j, city_i) = pheromone(city_j, city_i) + Q / best_length;
    end
    % 闭合路径
    city_i = best_path(end);
    city_j = best_path(1);
    pheromone(city_i, city_j) = pheromone(city_i, city_j) + Q / best_length;
    pheromone(city_j, city_i) = pheromone(city_j, city_i) + Q / best_length;
    
    %% 记录收敛信息
    convergence_curve(iter) = best_length;
    diversity_curve(iter) = calculate_diversity(ant_paths);
    
    %% 实时可视化
    subplot(1, 3, 1);
    plot_solution(cities, best_path, ant_paths, iter, best_length);
    
    subplot(1, 3, 2);
    plot(1:iter, convergence_curve(1:iter), 'b-', 'LineWidth', 2);
    xlabel('迭代次数');
    ylabel('最优路径长度');
    title('收敛曲线');
    grid on;
    
    subplot(1, 3, 3);
    plot(1:iter, diversity_curve(1:iter), 'r-', 'LineWidth', 2);
    xlabel('迭代次数');
    ylabel('解多样性');
    title('种群多样性');
    grid on;
    
    drawnow;
    
    % 显示迭代信息
    fprintf('迭代 %d/%d, 最优路径长度: %.4f, 多样性: %.4f\n', ...
            iter, max_iter, best_length, diversity_curve(iter));
    
    % 提前终止条件
    if iter > 20 && abs(convergence_curve(iter) - convergence_curve(iter-5)) < 1e-6
        fprintf('算法已收敛于第 %d 代\n', iter);
        break;
    end
end

%% 最终结果展示
fprintf('\n=== 蚁群算法优化结果 ===\n');
fprintf('最优路径: ');
fprintf('%d ', best_path);
fprintf('\n最优路径长度: %.6f\n', best_length);

%% 参数敏感性分析
figure('Position', [100, 100, 1200, 800]);
parameter_sensitivity_analysis(cities, dist_matrix);

%% 辅助函数定义
function path_length = calculate_path_length(path, dist_matrix)
    % 计算路径长度
    n = length(path);
    path_length = 0;
    for i = 1:(n-1)
        path_length = path_length + dist_matrix(path(i), path(i+1));
    end
    % 加上返回起点的距离
    path_length = path_length + dist_matrix(path(end), path(1));
end

function idx = roulette_wheel_selection(probabilities)
    % 轮盘赌选择
    r = rand();
    cumulative_prob = cumsum(probabilities);
    idx = find(r <= cumulative_prob, 1);
    if isempty(idx)
        idx = length(probabilities);
    end
end

function diversity = calculate_diversity(ant_paths)
    % 计算种群多样性（基于路径差异）
    n_ants = size(ant_paths, 1);
    diversity_sum = 0;
    count = 0;
    
    for i = 1:(n_ants-1)
        for j = (i+1):n_ants
            % 计算两条路径的差异
            diff_count = sum(ant_paths(i, :) ~= ant_paths(j, :));
            diversity_sum = diversity_sum + diff_count;
            count = count + 1;
        end
    end
    
    diversity = diversity_sum / count;
end

function plot_solution(cities, best_path, ant_paths, iter, best_length)
    % 绘制解决方案
    cla;
    hold on;
    
    % 绘制所有城市
    scatter(cities(:, 1), cities(:, 2), 100, 'blue', 'filled');
    
    % 绘制蚂蚁的路径（浅灰色）
    n_ants = size(ant_paths, 1);
    for k = 1:min(5, n_ants) % 只显示前5只蚂蚁的路径
        path = ant_paths(k, :);
        plot(cities(path, 1), cities(path, 2), 'Color', [0.8 0.8 0.8], 'LineWidth', 0.5);
        plot([cities(path(end), 1), cities(path(1), 1)], ...
             [cities(path(end), 2), cities(path(1), 2)], ...
             'Color', [0.8 0.8 0.8], 'LineWidth', 0.5);
    end
    
    % 绘制最优路径（红色加粗）
    plot(cities(best_path, 1), cities(best_path, 2), 'r-', 'LineWidth', 3);
    plot([cities(best_path(end), 1), cities(best_path(1), 1)], ...
         [cities(best_path(end), 2), cities(best_path(1), 2)], ...
         'r-', 'LineWidth', 3);
    
    % 标记起点
    start_city = best_path(1);
    scatter(cities(start_city, 1), cities(start_city, 2), 150, 'green', 'filled', 'pentagram');
    
    hold off;
    title(sprintf('蚁群优化过程 (迭代: %d)\n最优路径长度: %.4f', iter, best_length));
    xlabel('X坐标');
    ylabel('Y坐标');
    axis equal;
    grid on;
end

function parameter_sensitivity_analysis(cities, dist_matrix)
    % 参数敏感性分析
    n_cities = size(cities, 1);
    
    % 测试不同的参数组合
    alpha_values = [0.5, 1.0, 2.0];
    beta_values = [1.0, 2.0, 5.0];
    rho_values = [0.05, 0.1, 0.2];
    
    results = zeros(length(alpha_values), length(beta_values), length(rho_values));
    
    for a_idx = 1:length(alpha_values)
        for b_idx = 1:length(beta_values)
            for r_idx = 1:length(rho_values)
                alpha = alpha_values(a_idx);
                beta = beta_values(b_idx);
                rho = rho_values(r_idx);
                
                % 运行简化版ACO
                best_len = run_simple_aco(cities, dist_matrix, alpha, beta, rho);
                results(a_idx, b_idx, r_idx) = best_len;
                
                subplot_idx = (a_idx-1)*9 + (b_idx-1)*3 + r_idx;
                subplot(3, 9, subplot_idx);
                
                % 这里可以添加每个参数组合的可视化
                text(0.3, 0.5, sprintf('α=%.1f, β=%.1f, ρ=%.2f\n长度: %.3f', ...
                     alpha, beta, rho, best_len), 'FontSize', 8);
                axis off;
            end
        end
    end
    
    sgtitle('蚁群算法参数敏感性分析');
end

function best_length = run_simple_aco(cities, dist_matrix, alpha, beta, rho)
    % 简化版ACO用于参数测试
    n_cities = size(cities, 1);
    n_ants = 20;
    max_iter = 50;
    Q = 1.0;
    tau0 = 0.1;
    
    % 初始化
    pheromone = tau0 * ones(n_cities, n_cities);
    heuristic = 1 ./ (dist_matrix + eye(n_cities));
    
    best_path = [];
    best_length = inf;
    
    for iter = 1:max_iter
        for k = 1:n_ants
            path = build_ant_path(pheromone, heuristic, alpha, beta, n_cities);
            path_length = calculate_path_length(path, dist_matrix);
            
            if path_length < best_length
                best_length = path_length;
                best_path = path;
            end
        end
        
        % 信息素更新
        pheromone = (1 - rho) * pheromone;
        for i = 1:(n_cities-1)
            city_i = best_path(i);
            city_j = best_path(i+1);
            pheromone(city_i, city_j) = pheromone(city_i, city_j) + Q / best_length;
            pheromone(city_j, city_i) = pheromone(city_j, city_i) + Q / best_length;
        end
    end
end

function path = build_ant_path(pheromone, heuristic, alpha, beta, n_cities)
    % 单只蚂蚁构建路径
    path = zeros(1, n_cities);
    visited = false(1, n_cities);
    
    current_city = randi(n_cities);
    path(1) = current_city;
    visited(current_city) = true;
    
    for step = 2:n_cities
        allowed_cities = find(~visited);
        probabilities = zeros(1, length(allowed_cities));
        
        for idx = 1:length(allowed_cities)
            j = allowed_cities(idx);
            probabilities(idx) = pheromone(current_city, j)^alpha * ...
                                heuristic(current_city, j)^beta;
        end
        
        if sum(probabilities) > 0
            probabilities = probabilities / sum(probabilities);
        else
            probabilities = ones(1, length(allowed_cities)) / length(allowed_cities);
        end
        
        next_city_idx = roulette_wheel_selection(probabilities);
        next_city = allowed_cities(next_city_idx);
        
        path(step) = next_city;
        visited(next_city) = true;
        current_city = next_city;
    end
end

运行说明

将代码保存为

aco_tsp.m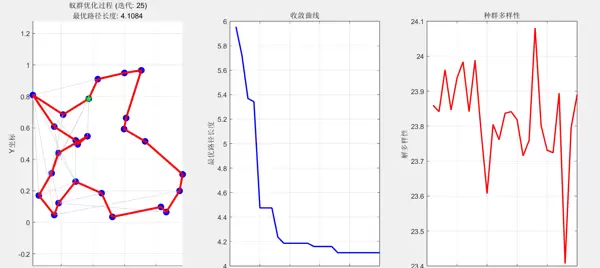

文件，在MATLAB中直接运行该脚本。运行后将生成3个可视化窗口：

• 主优化过程动态图（路径演化）
• 收敛曲线图
• 参数敏感性分析图（原代码只运行一次秒出结果，但因为每次运行都是随机的，因此下面为了更好地反映不同参数的性能进行了多次求平均）

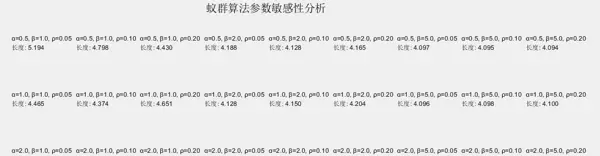
结果解读与技术价值

可视化结果的意义

在路径演化图中：

• 蓝色圆点代表各个城市的位置
• 浅灰色线条显示部分蚂蚁的当前路径
• 红色粗线标记当前找到的最优路径
• 绿色五角星标记路径起点

从动画中可以看到，最初蚂蚁的路径非常混乱，但随着迭代的进行，逐渐收敛到一条相对平滑的最优路径。

收敛曲线显示了算法性能随迭代次数的提升过程，体现了正反馈机制的学习效果。

多样性曲线反映了种群中解的差异程度，良好的算法应该在探索初期保持高多样性，在后期适当收敛。

参数敏感性分析的意义

不同参数组合对算法性能的影响：

• α过大：过度依赖信息素，容易早熟收敛
• β过大：过度依赖启发信息，类似贪婪算法
• ρ过小：信息素挥发慢，收敛速度慢
• ρ过大：信息素挥发快，难以积累经验

应用场景与扩展思考

实际工程应用

蚁群算法已成功应用于多个领域：

• 物流配送：车辆路径规划、配送中心选址
• 网络路由：通信网络中的最优路径选择
• 调度问题：生产调度、任务分配等

算法哲学思考

蚁群算法不仅是一种技术工具，更是对自然界智慧的一种深刻理解和模仿。通过模拟蚂蚁的行为，我们不仅解决了实际问题，也启发了对复杂系统和群体智能的深入思考。

结语：自然智慧的数学颂歌

单只蚂蚁的路径是随机的，但蚁群的路径却是最优的——这就是群体智能的魅力所在。通过学习自然界的智慧，我们能够在解决复杂问题时找到更加高效和优雅的方法。

作业车间调度、任务分配

在制造业中，作业车间调度和任务分配是提高生产效率的关键环节。合理安排生产任务和资源，能够有效减少等待时间和提高设备利用率。

图像处理

图像处理技术广泛应用于多个领域，其中图像边缘检测和特征选择是两个重要的步骤。通过这些技术，可以提取图像中的关键信息，为后续的分析和识别提供支持。

算法哲学思考

蚁群算法展示了简单个体通过局部交互产生群体智能的涌现现象。每只蚂蚁遵循简单的规则，但整个群体却能解决复杂的问题。这一现象启示我们，解决复杂问题不一定需要复杂的个体，而是可以通过设计良好的协作机制来实现。

结语：自然智慧的数学颂歌

从林间蚂蚁的觅食行为到组合优化问题的高效求解，蚁群算法展示了自然智慧与数学优雅的完美结合。它告诉我们，最优解往往不是通过集中控制找到的，而是通过分布式协作自然涌现的。

在人工智能快速发展的今天，蚁群算法在优化问题的广阔领域中继续发挥着独特的作用。它提醒我们，有时最先进的解决方案就隐藏在最普通的自然现象中。

算法如同蚁群，在问题的森林中以协作为路径，以正反馈为引导，最终开辟出通往最优解的光明大道。

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：Optimization Convergence Sensitivity cumulative Abilities