在计算机中,各种数值的表示形式被称为机器数。其主要特点包括采用二进制计数系统,数的符号通过0和1来表示(0为正,1为负),而小数点则是隐含存在的,并不占用实际存储位置。与机器数相对应的实际数值称为该数的真值。

常见的编码方式
原码表示法
在原码中,机器数的最高位作为符号位:0表示正数,1表示负数;其余各位则直接表示数值的绝对值部分。
值得注意的是,零在原码中有两种不同的表示形式:[+0]原 = 00000000,[-0]原 = 10000000。
优点:原码与真值之间的转换非常直观、简便。
缺点:加减运算过程复杂,必须先判断符号位,导致硬件设计难度增加;同时存在+0和-0两种零的表示,影响运算一致性。
示例:假设字长为8位

反码表示法
反码同样将最高位设为符号位(0为正,1为负)。当符号位为0时,其余位即为该数的二进制值;若符号位为1,则其余位需进行按位取反操作,才能得到对应的二进制数值。
零在此表示法中也有两个编码:[+0]反 = 00000000,[-0]反 = 11111111。
优点:符号位可以参与运算,在一定程度上简化了部分加减操作。
缺点:依然存在正零与负零的问题,且在执行加减运算时需要处理循环进位,硬件实现较为复杂。
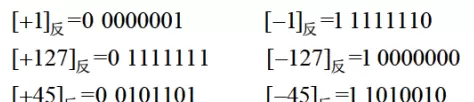
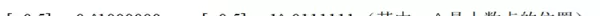
补码表示法
补码是在反码基础上进一步改进的一种编码方式。对于正数(符号位为0),其补码与原码、反码相同;而对于负数(符号位为1),则需先对数值位按位取反,再在最低位加1。
补码最大的优势之一是:零仅有唯一的表示形式,即[+0]补 = [-0]补 = 00000000。
优点:在进行加法运算时,只要结果未超出机器所能表示的范围,符号位可与数值位一并处理,无需单独判断符号,极大简化了运算逻辑。
缺点:数值表示范围不对称(如8位补码范围为-128到127);负数转换成补码的过程稍显繁琐,需执行取反加一操作。

移码表示法
移码通常由补码的符号位取反获得,因此它也具有唯一的零表示方式。
优点:常用于浮点数中的阶码表示,便于直接使用无符号比较的方式来判断数值大小,从而简化浮点运算的控制逻辑。
缺点:应用范围有限,主要用于特定场景(如浮点数阶码),不能直接用于一般整数运算,且需要额外的编码转换步骤。

定点数与浮点数
定点数
定点数是指小数点位置固定不变的数值表示方法。通常有两种约定方式:
- 定点整数:纯整数形式,小数点位于最低有效位之后。
- 定点小数:纯小数形式,小数点置于最高有效位之前。

浮点数
浮点数允许小数点的位置浮动,因而能够表示更广范围的数值。例如十进制数83.125可表示为10×0.083125或10×0.0083125等形式。
在浮点表示中,一个数通常分解为两部分:阶码E(带符号整数)和尾数M(带符号小数)。其一般表达式如下:

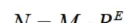
其中:
- M:尾数,决定了浮点数的精度。为了充分利用尾数位,通常采用规格化浮点数,即将尾数的绝对值限制在区间[0.5, 1)之内。这一区间的设定源于二进制特性——0.5的二进制为0.1,因此规格化要求尾数的小数点后第一位必须为1。
- R:基数,通常是2或10。
- E:阶码,决定小数点的实际位置,进而影响数值的表示范围。若超出机器可表示范围,则发生溢出。
若浮点数的阶码(含1位阶符)用R位移码表示,尾数(含1位数符)用M位补码表示,则其能表示的数值范围如下(参考前述定点数各码制的取值规则):
最大正数:
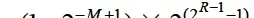
最小负数:
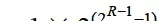
IEEE 754 浮点数标准
IEEE 754 是由电气与电子工程师协会(IEEE)制定的浮点数表示工业标准,被广泛应用于现代计算机系统中。其基本格式如下:
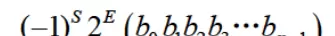
结构说明:
- S:数符位,S=0表示正数,S=1表示负数。
- E:指数部分(阶码),采用移码表示。
- M:尾数部分,长度为P位,采用原码表示。

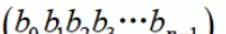
当前计算机中主要支持三种符合IEEE 754标准的浮点数格式:





 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







