在工程与材料科学领域,脆性断裂的数值模拟一直是研究的重点方向之一。有限单元相场法作为一种先进的模拟手段,能够有效处理复杂裂纹的萌生与扩展问题,而无需显式追踪裂纹路径。本文将介绍如何利用MATLAB实现该方法的基本框架,涵盖弹性方程与相场方程的耦合求解过程,并支持增量加载条件下的逐步演化分析。
 相场法的核心思想是引入一个连续变量来表征材料的断裂状态。该变量在未受损区域取值为1,在完全断裂区域降为0,中间值则表示过渡性的损伤带。通过这种方式,原本不连续的裂纹被平滑地表达为相场变量的空间分布,从而避免了对裂纹几何形态的直接建模。
相场法的核心思想是引入一个连续变量来表征材料的断裂状态。该变量在未受损区域取值为1,在完全断裂区域降为0,中间值则表示过渡性的损伤带。通过这种方式,原本不连续的裂纹被平滑地表达为相场变量的空间分布,从而避免了对裂纹几何形态的直接建模。
 在具体实现中,整个求解流程基于有限元方法展开。首先对位移场
在具体实现中,整个求解流程基于有限元方法展开。首先对位移场
 重点来看
重点来看
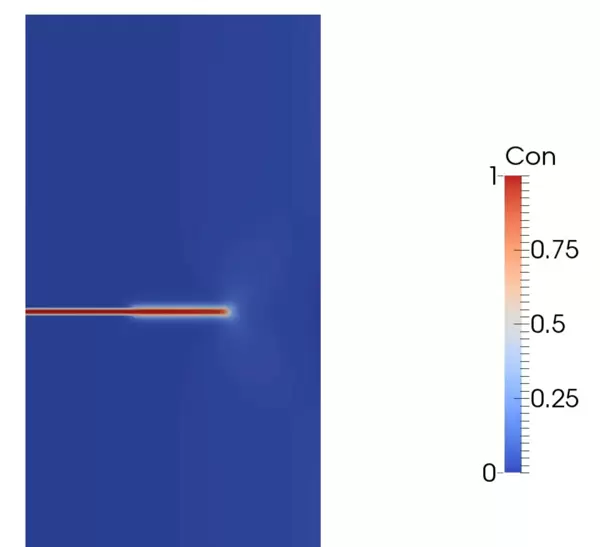 再看
再看
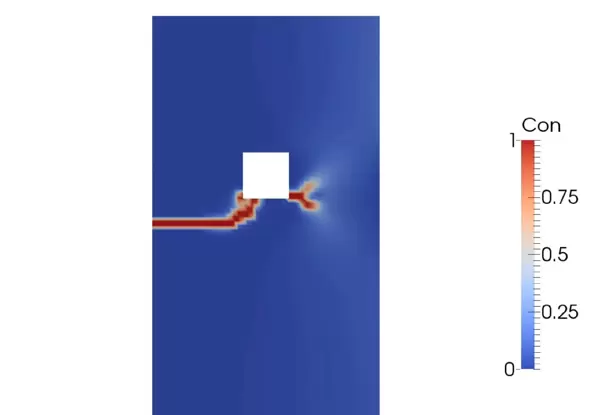 综上所述,基于MATLAB平台的有限单元相场法虽然涉及多个数学与力学概念的融合,但其编程实现具有良好的模块化特性,逻辑清晰且易于扩展。通过对微裂纹起始、扩展路径及分叉行为的稳定模拟,该方法为复杂断裂问题提供了强有力的数值工具。读者可在此基础上进一步加入各向异性损伤模型或多物理场耦合机制,提升模拟的真实性与适用范围。
综上所述,基于MATLAB平台的有限单元相场法虽然涉及多个数学与力学概念的融合,但其编程实现具有良好的模块化特性,逻辑清晰且易于扩展。通过对微裂纹起始、扩展路径及分叉行为的稳定模拟,该方法为复杂断裂问题提供了强有力的数值工具。读者可在此基础上进一步加入各向异性损伤模型或多物理场耦合机制,提升模拟的真实性与适用范围。
 相场法的核心思想是引入一个连续变量来表征材料的断裂状态。该变量在未受损区域取值为1,在完全断裂区域降为0,中间值则表示过渡性的损伤带。通过这种方式,原本不连续的裂纹被平滑地表达为相场变量的空间分布,从而避免了对裂纹几何形态的直接建模。
相场法的核心思想是引入一个连续变量来表征材料的断裂状态。该变量在未受损区域取值为1,在完全断裂区域降为0,中间值则表示过渡性的损伤带。通过这种方式,原本不连续的裂纹被平滑地表达为相场变量的空间分布,从而避免了对裂纹几何形态的直接建模。
 在具体实现中,整个求解流程基于有限元方法展开。首先对位移场
在具体实现中,整个求解流程基于有限元方法展开。首先对位移场
uphifunction [u, phi] = phaseFieldFracture(nelx, nely, E, nu, Gc, l)
% nelx, nely: 单元数量
% E: 弹性模量
% nu: 泊松比
% Gc: 断裂能
% l: 相场长度尺度参数
% 初始化位移场和相场
u = zeros(2*(nelx+1)*(nely+1), 1);
phi = ones((nelx+1)*(nely+1), 1);
% 增量外部载荷
for loadStep = 1:10
% 计算弹性应变能
strainEnergy = computeStrainEnergy(u, nelx, nely, E, nu);
% 更新相场变量
phi = updatePhaseField(phi, strainEnergy, Gc, l);
% 求解位移场
u = solveDisplacement(u, phi, nelx, nely, E, nu);
end
endcomputeStrainEnergyupdatePhaseFieldsolveDisplacement 重点来看
重点来看
updatePhaseFieldfunction phi = updatePhaseField(phi, strainEnergy, Gc, l)
% 更新相场变量
for i = 1:length(phi)
if strainEnergy(i) > Gc / (2 * l)
phi(i) = 0;
else
phi(i) = 1 - strainEnergy(i) * 2 * l / Gc;
end
end
end 再看
再看
solveDisplacementfunction u = solveDisplacement(u, phi, nelx, nely, E, nu)
% 求解位移场
K = assembleStiffnessMatrix(phi, nelx, nely, E, nu);
F = assembleLoadVector(nelx, nely);
u = K \ F;
endKFK * u = Fu 综上所述,基于MATLAB平台的有限单元相场法虽然涉及多个数学与力学概念的融合,但其编程实现具有良好的模块化特性,逻辑清晰且易于扩展。通过对微裂纹起始、扩展路径及分叉行为的稳定模拟,该方法为复杂断裂问题提供了强有力的数值工具。读者可在此基础上进一步加入各向异性损伤模型或多物理场耦合机制,提升模拟的真实性与适用范围。
综上所述,基于MATLAB平台的有限单元相场法虽然涉及多个数学与力学概念的融合,但其编程实现具有良好的模块化特性,逻辑清晰且易于扩展。通过对微裂纹起始、扩展路径及分叉行为的稳定模拟,该方法为复杂断裂问题提供了强有力的数值工具。读者可在此基础上进一步加入各向异性损伤模型或多物理场耦合机制,提升模拟的真实性与适用范围。



 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







