方差分析(ANOVA)简介
方差分析,也被称为“变异数分析”或“F检验”,是由统计学家罗纳德·费雪爵士提出的一种统计方法,主要用于判断两个或多个样本均值之间是否存在显著差异。相较于T检验仅适用于两组数据的比较,方差分析能够处理多组数据的情形,因此在实际研究中具有更广泛的应用价值。
方差分析的前提条件
- 独立性:各组观测数据相互独立,不存在关联。
- 正态性:每组数据应大致符合正态分布。
- 方差齐性:不同组之间的方差应近似相等。
因素与水平的概念解析
在统计学中,“因素”指的是实验中研究者关注的影响变量,而“水平”则是指该因素的具体取值或分类方式。例如,在研究温度对反应速率的影响时,若设定温度为30℃、45℃、60℃和90℃,则“温度”是因素,这四个数值即为其对应的水平;同理,若考察产地(如陕西、河北、山东)对农产品品质的影响,则“产地”为因素,各地名称为相应的水平。
单因素方差分析概述
当仅考虑一个控制变量对结果变量的影响时,所采用的方法称为单因素方差分析。这种方法旨在检验该控制变量的不同水平是否对观测结果产生了统计意义上的显著影响。
典型应用场景包括:
- 探究不同施肥量对农作物产量的影响;
- 分析地区差异是否影响女性生育率;
- 研究教育程度如何作用于个人收入水平。
其中,农作物产量、生育率、工资收入属于观测变量,而施肥量、地区、学历则作为控制变量。
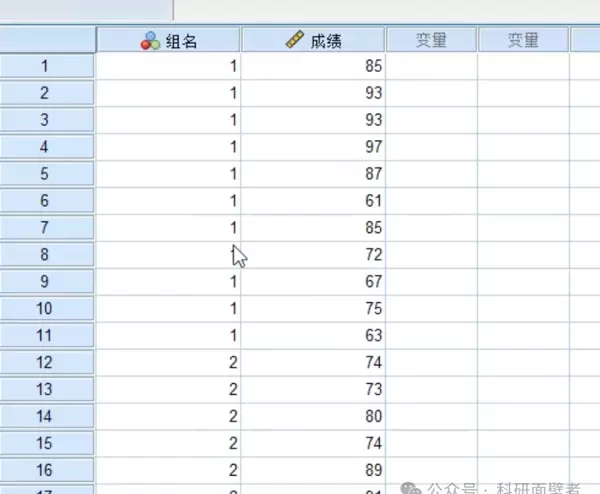
案例分析:课堂笔记对学生学习成绩的影响
为了验证做笔记的行为是否会影响学生的考试成绩,我们进行一次单因素方差分析。以下是相关数据与操作流程。

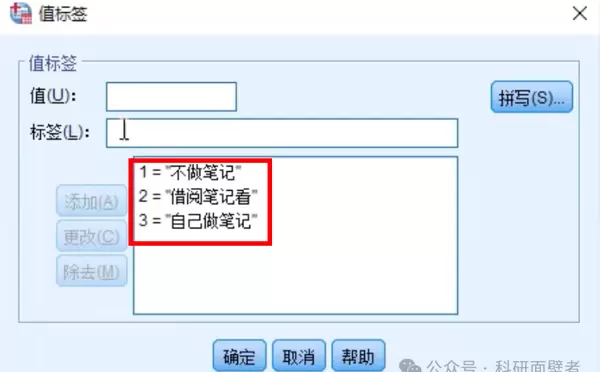
正态性检验
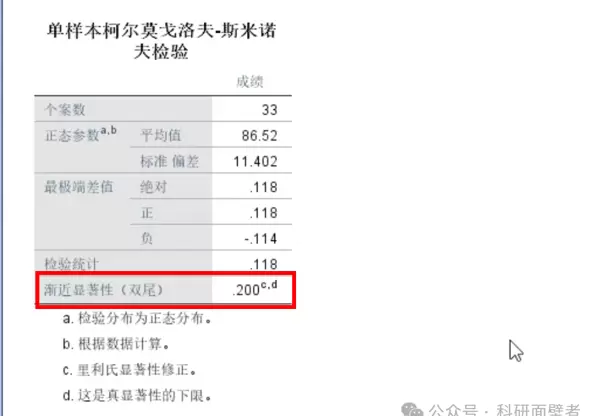
在执行方差分析前,首先需确认成绩这一变量是否服从正态分布。
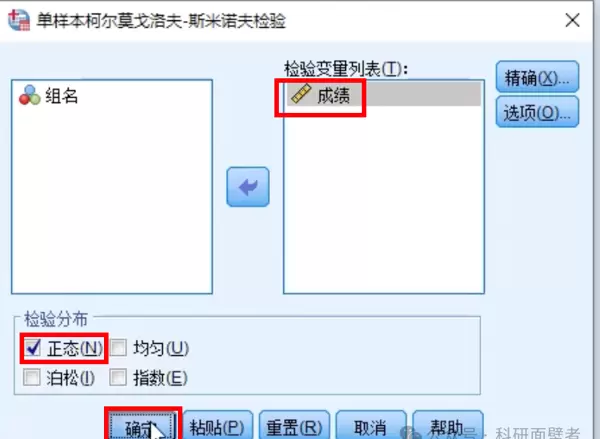
结果显示,检验的显著性大于0.05,表明成绩数据满足正态性假设,可以继续开展后续分析。
实施单因素方差分析
接下来进入正式的方差分析步骤。
在设置过程中,“对比”功能可用于多项式趋势检验,本例中不涉及趋势对比,故无需勾选。
事后多重比较
虽然方差分析能判断控制变量整体上是否对观测变量有显著影响,但无法明确指出具体哪两个水平间存在差异。为此,需要借助事后比较方法进一步分析各水平间的均值差异。
常用的事后检验方法包括:
- LSD法(最小显著差异法):灵敏度较高,即使均值间仅有微小差别也可能被检测出,但容易增加第一类错误的风险。
- 邦弗伦尼校正法:基于LSD方法改进而来,通过调整显著性水平来控制多重比较带来的误差累积,标准更为严格。
- 图基HSD法(Tukey's HSD):广泛应用于质量控制领域,其优势在于计算简便且所需样本量较小。在95%置信水平下,最少只需6个样本即可完成有效验证(改善前后各3个),适合一线人员使用。
- S-N-K法:适用于各组样本数量相等的情况,擅长将相似均值的组归入同一子集。
本案例选择图基HSD、LSD及邦弗伦尼三种方法进行两两比较:
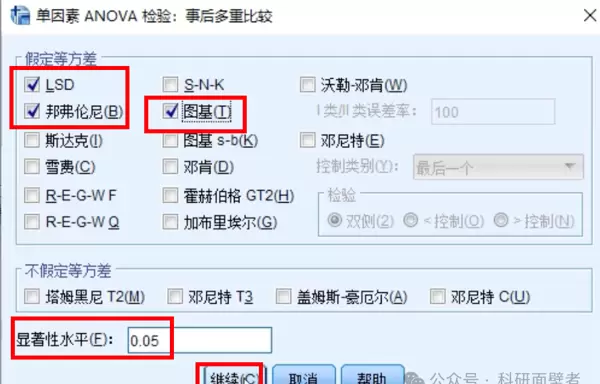
选项设置
在“选项”菜单中,勾选描述性统计、方差齐性检验以及均值图等输出内容,以便全面评估结果。
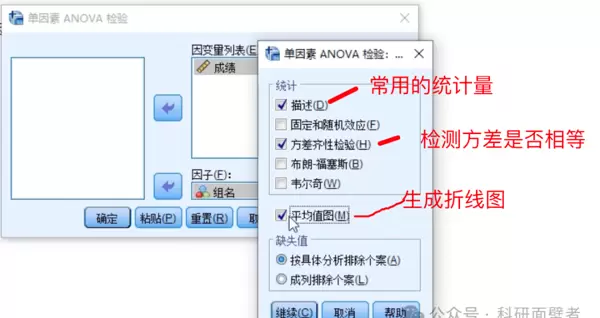
结果解读
点击确定后,得到以下分析结果:
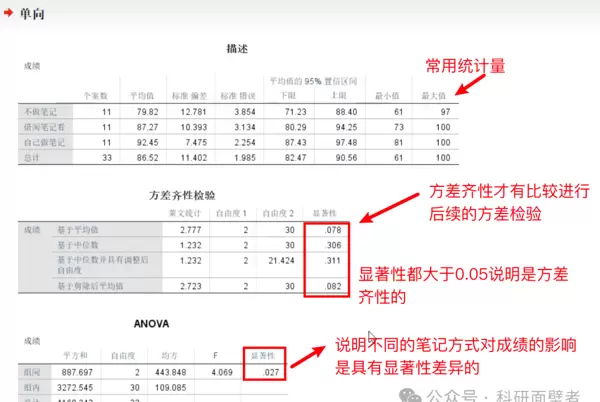
- 从描述性统计表可知,不做笔记、借阅笔记和自己做笔记三组的学生人数均为11人。
- 方差齐性检验显示显著性值大于0.05,说明各组方差齐性成立,满足方差分析的基本前提。
- ANOVA表中的显著性小于0.05,表明三组之间的平均成绩存在显著差异。
多重比较结果分析
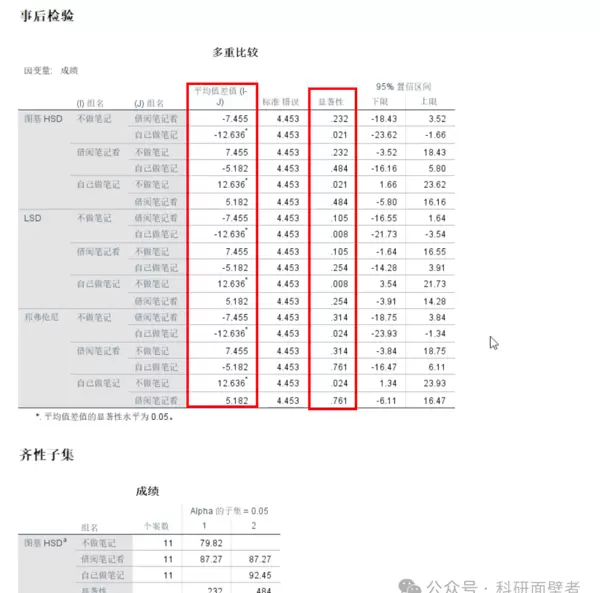
从事后比较结果可以看出:
- 无论是图基HSD、LSD还是邦弗伦尼方法,不做笔记组与其他两组相比,其平均值差均为负数,说明记笔记(无论自行记录或借阅)的学生平均成绩更高,且差值越大表示提升越明显。
- 在显著性方面:
- 不做笔记 vs 借阅笔记:p > 0.05,无显著差异;
- 不做笔记 vs 自己做笔记:p < 0.05,存在显著差异;
- 借阅笔记 vs 自己做笔记:p > 0.05,两者无显著差异。
均值变化趋势图
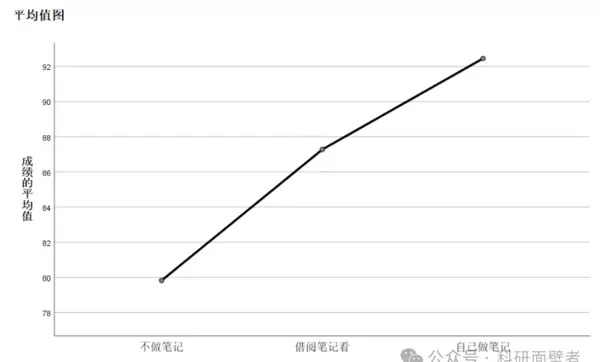
从均值图可直观看出,随着学习行为从“不做笔记”到“借阅笔记”再到“自己做笔记”,学生成绩的平均值呈现逐步上升的趋势。
综上所述,本研究表明:是否参与笔记活动对学生学业表现具有显著影响,尤其是主动自己做笔记的学生,其成绩显著优于不做笔记者。尽管借阅笔记也能带来一定提升,但与自主记笔记相比并无统计学上的显著优势。




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







