发帖
雷达卡
在电力系统中，合理规划分布式电源（DG）的选址与容量配置对提升电网运行效率、降低综合成本具有重要意义。本文以IEEE33节点系统为研究对象，采用改进自适应遗传算法，以年最小综合成本为目标函数，结合四项关键约束条件，实现DG的优化配置。
系统中各节点的有功与无功功率必须保持动态平衡。以有功功率为例，在节点 \( i \) 处满足： \[ P_{i,G} - P_{i,L} - \sum_{j \in \Omega_i} P_{ij} = 0 \] 其中，\( P_{i,G} \) 为节点 \( i \) 上DG输出的有功功率，\( P_{i,L} \) 为该节点负荷需求，\( \Omega_i \) 表示与节点 \( i \) 相连的所有邻接节点集合，\( P_{ij} \) 为从节点 \( i \) 流向 \( j \) 的有功功率。
2. 电压约束
各节点电压幅值应处于允许范围内，避免出现过压或欠压现象： \[ V_{i,min} \leq V_i \leq V_{i,max} \] 其中，\( V_i \) 为节点 \( i \) 的实际电压，\( V_{i,min} \) 和 \( V_{i,max} \) 分别为其上下限值。 3. 线路容量约束
为防止线路过载，流经任意支路的功率不得超过其额定传输能力。对于连接节点 \( i \) 与 \( j \) 的线路，有： \[ |P_{ij}| \leq P_{ij,max} \] 其中，\( P_{ij,max} \) 为该线路所能承受的最大有功功率。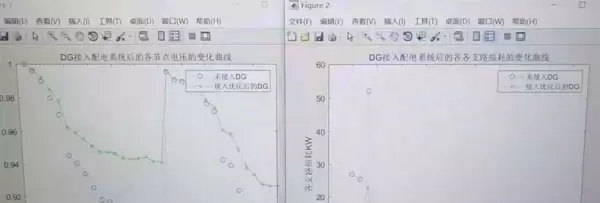
4. DG容量约束
每个候选节点上安装的DG容量需在其技术允许范围内： \[ S_{DG,i,min} \leq S_{DG,i} \leq S_{DG,i,max} \] 其中，\( S_{DG,i} \) 为节点 \( i \) 处DG的实际接入容量，\( S_{DG,i,min} \) 与 \( S_{DG,i,max} \) 分别为其最小和最大允许值。
采用实数编码策略来表征潜在解决方案。设系统中有 \( n \) 个可选节点用于接入DG，则使用一个长度为 \( n \) 的数组进行编码，数组中每个元素代表对应节点的DG接入容量；若某元素为0，则表示该节点未接入DG。
适应度函数直接基于目标函数构建，即计算每个个体对应的年综合成本。由于目标是最小化成本，因此适应度值取为成本的倒数或负值形式处理，使成本越低的个体具有更高的适应度。
采用轮盘赌选择机制，依据个体适应度分配被选中的概率。适应度越高，入选下一代的概率越大，从而保留优质基因。
引入单点交叉策略，随机选取两个父代个体，并在其染色体上选定一个交叉位置，交换该点之后的所有基因片段，生成两个新的子代个体，增强解空间探索能力。
为维持种群多样性并避免早熟收敛，设定一定变异率，对个体中部分基因进行随机扰动。例如，对某个非零容量节点的数值进行小幅调整，或在原为0的节点引入微小容量尝试新布局。
根据算法收敛后的最优编码结果，识别出实际接入DG的节点及其对应容量。例如，编码数组中非零元素的位置即为推荐接入点，其数值即为建议安装容量。 2. 迭代过程可视化
绘制算法迭代过程中每一代最优个体的成本变化曲线，直观展示收敛趋势与稳定性。通常使用绘图工具生成迭代图，反映优化进程。
进一步输出接入前后系统的各项指标变化，包括： - 各支路有功损耗的变化曲线； - 所有节点电压幅值的分布对比图； - 年综合成本构成的详细分解数据。 这些结果共同验证了所提方法在降低运行成本、改善电压质量与减少网络损耗方面的有效性。
一、目标函数：年最小综合成本
本研究将年综合成本作为优化目标，综合考虑投资、运行维护及网损等因素。目标函数可表示为： \[ C_{total} = C_{investment} + C_{operation} + C_{loss} \] 其中，\( C_{investment} \) 表示分布式电源的初始投资成本，\( C_{operation} \) 为其运行与维护支出，而 \( C_{loss} \) 则反映接入DG后系统功率损耗所引起的经济代价。通过最小化该总成本，可获得最优的选址定容方案。
二、系统约束条件
为确保配电网在接入DG后的安全稳定运行，需满足以下四类基本约束： 1. 功率平衡约束系统中各节点的有功与无功功率必须保持动态平衡。以有功功率为例，在节点 \( i \) 处满足： \[ P_{i,G} - P_{i,L} - \sum_{j \in \Omega_i} P_{ij} = 0 \] 其中，\( P_{i,G} \) 为节点 \( i \) 上DG输出的有功功率，\( P_{i,L} \) 为该节点负荷需求，\( \Omega_i \) 表示与节点 \( i \) 相连的所有邻接节点集合，\( P_{ij} \) 为从节点 \( i \) 流向 \( j \) 的有功功率。
2. 电压约束各节点电压幅值应处于允许范围内，避免出现过压或欠压现象： \[ V_{i,min} \leq V_i \leq V_{i,max} \] 其中，\( V_i \) 为节点 \( i \) 的实际电压，\( V_{i,min} \) 和 \( V_{i,max} \) 分别为其上下限值。 3. 线路容量约束
为防止线路过载，流经任意支路的功率不得超过其额定传输能力。对于连接节点 \( i \) 与 \( j \) 的线路，有： \[ |P_{ij}| \leq P_{ij,max} \] 其中，\( P_{ij,max} \) 为该线路所能承受的最大有功功率。
4. DG容量约束每个候选节点上安装的DG容量需在其技术允许范围内： \[ S_{DG,i,min} \leq S_{DG,i} \leq S_{DG,i,max} \] 其中，\( S_{DG,i} \) 为节点 \( i \) 处DG的实际接入容量，\( S_{DG,i,min} \) 与 \( S_{DG,i,max} \) 分别为其最小和最大允许值。
三、改进自适应遗传算法的应用
1. 编码方式采用实数编码策略来表征潜在解决方案。设系统中有 \( n \) 个可选节点用于接入DG，则使用一个长度为 \( n \) 的数组进行编码，数组中每个元素代表对应节点的DG接入容量；若某元素为0，则表示该节点未接入DG。
# 示例编码，假设系统有33个节点
import numpy as np
num_nodes = 33
chromosome = np.random.uniform(0, 100, num_nodes) # 随机生成0到100之间的容量值，实际需根据容量约束调整范围numpy适应度函数直接基于目标函数构建，即计算每个个体对应的年综合成本。由于目标是最小化成本，因此适应度值取为成本的倒数或负值形式处理，使成本越低的个体具有更高的适应度。
def fitness_function(chromosome):
# 这里简单模拟计算成本，实际需根据具体成本公式计算
cost = np.sum(chromosome) # 假设成本与总容量成正比，实际需综合考虑投资、运行等成本
return 1 / cost # 适应度为成本的倒数，成本越低适应度越高采用轮盘赌选择机制，依据个体适应度分配被选中的概率。适应度越高，入选下一代的概率越大，从而保留优质基因。
def roulette_wheel_selection(population, fitness_values):
total_fitness = np.sum(fitness_values)
selection_probabilities = fitness_values / total_fitness
selected_indices = np.random.choice(len(population), size=len(population), p=selection_probabilities)
selected_population = [population[i] for i in selected_indices]
return selected_population引入单点交叉策略，随机选取两个父代个体，并在其染色体上选定一个交叉位置，交换该点之后的所有基因片段，生成两个新的子代个体，增强解空间探索能力。
def single_point_crossover(parent1, parent2):
crossover_point = np.random.randint(1, len(parent1) - 1)
child1 = np.concatenate((parent1[:crossover_point], parent2[crossover_point:]))
child2 = np.concatenate((parent2[:crossover_point], parent1[crossover_point:]))
return child1, child2为维持种群多样性并避免早熟收敛，设定一定变异率，对个体中部分基因进行随机扰动。例如，对某个非零容量节点的数值进行小幅调整，或在原为0的节点引入微小容量尝试新布局。
def mutation(chromosome, mutation_rate):
for i in range(len(chromosome)):
if np.random.rand() < mutation_rate:
chromosome[i] = np.random.uniform(0, 100) # 随机改变容量值，实际需根据容量约束调整范围
return chromosome四、仿真结果分析
通过对IEEE33节点系统实施上述优化流程，最终可获得以下成果： 1. 分布式电源的最佳接入位置与容量根据算法收敛后的最优编码结果，识别出实际接入DG的节点及其对应容量。例如，编码数组中非零元素的位置即为推荐接入点，其数值即为建议安装容量。 2. 迭代过程可视化
绘制算法迭代过程中每一代最优个体的成本变化曲线，直观展示收敛趋势与稳定性。通常使用绘图工具生成迭代图，反映优化进程。
matplotlib进一步输出接入前后系统的各项指标变化，包括： - 各支路有功损耗的变化曲线； - 所有节点电压幅值的分布对比图； - 年综合成本构成的详细分解数据。 这些结果共同验证了所提方法在降低运行成本、改善电压质量与减少网络损耗方面的有效性。
成本计算：
在确定最终方案后，需对年综合成本进行核算，以检验其是否实现了最小化的目标。
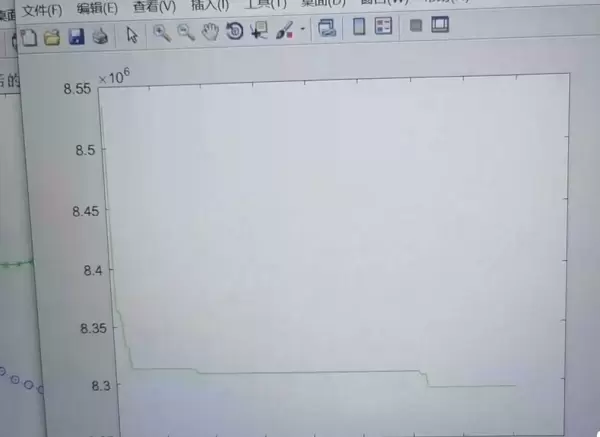
各支路损耗及节点电压变化曲线分析：
通过对比分布式电源（DG）接入前后系统中各支路的功率损耗以及各节点电压的变化曲线，可以有效评估DG接入对整体系统性能的影响。重点考察其对网络损耗的降低效果和对电压稳定性的改善作用。
import matplotlib.pyplot as plt
# 假设已经得到每次迭代的成本值列表cost_history
plt.plot(range(len(cost_history)), cost_history)
plt.xlabel('Iteration')
plt.ylabel('Cost')
plt.title('Convergence Curve')
plt.show()上述曲线可借助以下图形工具进行绘制，例如支路损耗变化趋势图：
matplotlib# 假设已经得到DG接入前后各支路损耗列表before_losses, after_losses
num_branches = len(before_losses)
branch_indices = range(num_branches)
plt.bar(np.array(branch_indices) - 0.2, before_losses, width=0.4, label='Before DG')
plt.bar(np.array(branch_indices) + 0.2, after_losses, width=0.4, label='After DG')
plt.xlabel('Branch Index')
plt.ylabel('Power Loss')
plt.title('Branch Power Loss Comparison')
plt.legend()
plt.show()总结：
通过遗传算法的应用，本文完成了在IEEE33节点系统中对分布式电源的选址与定容优化分析。该方法为提升电力系统的运行效率与稳定性提供了有效的技术支撑。希望本研究能为相关领域的工程实践与学术探索提供有价值的参考。
京公网安备 11010802022788号
