一、二重积分的定义
定积分与二重积分都具有明确的几何意义。要深入理解二重积分的概念及其计算方式,首先需要掌握其定义的本质。
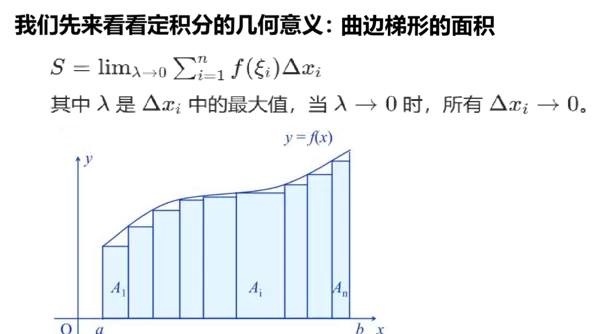

在定义中涉及面积元的概念。由于我们将底面通过类似网格的方式划分为N个微小区域,因此dx*dy即表示每个微小部分的面积单元,也就是面积元素。
二、二重积分的计算方法及原理
若将二重积分视为一个曲顶柱体的体积表达式,而我们尚未掌握直接积分的方法,那么是否可以通过其他途径来求得该体积?只要能够算出体积,就等于找到了一种可行的二重积分计算路径。
(1)x型区域
当所讨论的曲顶柱体沿垂直于x轴方向的两个侧面为平面,且无弯曲时,整个结构可看作由无数个截面沿x轴堆叠而成的曲边梯形体。
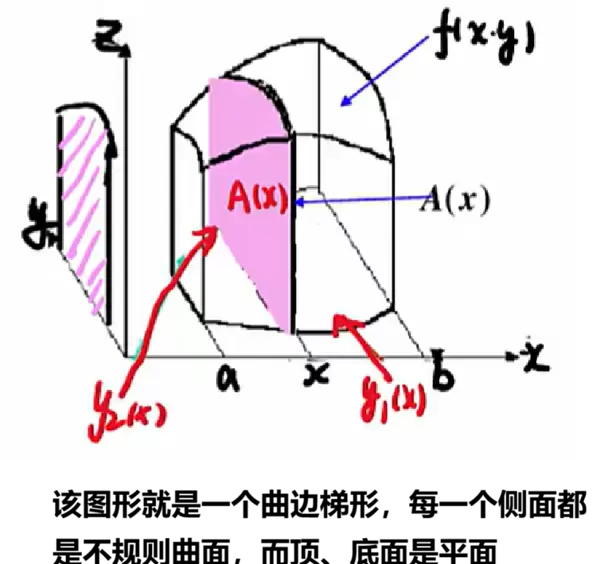
对于此类图形,自然想到的方法是:沿垂直于x轴的方向切开,形成一系列截面。每个截面乘以dx(相当于高度),得到该截面的微体积,再对所有微体积进行累加并取极限即可得出总体积。在此过程中,每一截面内x保持不变,仅y和z发生变化。

由此,二重积分被转化为二次积分:第一次积分用于求解截面面积的表达式,第二次积分则是将这些面积沿x方向叠加,最终获得体积。由于积分顺序为先对y积分、后对x积分,故也称“先y后x”型。
值得注意的是,在对y积分的过程中,x被视为常量处理。这是因为在垂直于x轴的截面上,x值始终固定,这也是解决此类问题的关键技巧之一。
(2)y型区域
类似地,若物体在y方向上具有两个平行平面,即上下底面为平面、侧边为曲面的几何体,则可通过沿垂直于y轴切割成多个截面,并对其面积进行积分求和的方式来计算体积。
此处不再详细推导过程,直接给出对应的积分公式:
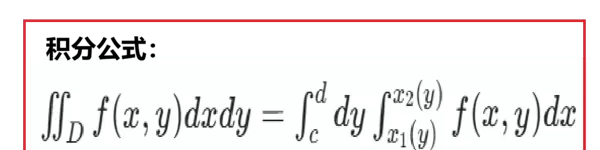
(3)极坐标型
无论是x型还是y型区域,通常要求物体至少存在两个平行平面才能应用截面叠加法。然而现实中的许多几何体并不满足这一条件,例如球体——其表面各处均不平行。那么这类情况是否仍能使用类似思路求解?
答案是肯定的,但需转换坐标系。我们之前所说的“平行”概念基于直角坐标系,属于常规理解下的平行关系。但如果改用极坐标系,以共中心点、不同半径的圆周或球面来看,它们之间也可以视为某种意义上的“平行”。
因此,极坐标下的处理方式与x型、y型区域本质一致,同样是利用截面叠加思想来求解体积。

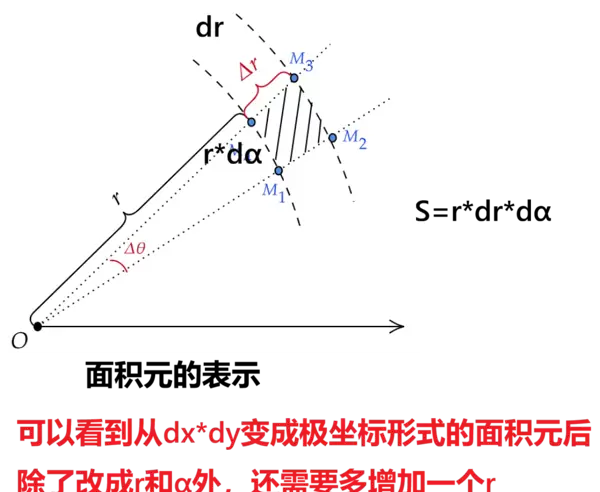
一般而言,当变量x与y之间的关系呈现圆形、椭圆或其他与极坐标相关的形式,且无法有效划分为x型或y型区域时,采用极坐标方法更为合适。
(4)总结
- 二重积分本质上反映的是某一空间立体的体积。根据积分区域的不同特征,可分为x型、y型以及极坐标型。尽管形式各异,但核心思想均为通过截面叠加求体积,三者本质相通。
- 虽然二重积分最初从体积角度引入,但其应用范围远不止于此。函数f(x, y)在具体场景中可能代表密度、温度或其他物理量。无论何种含义,一旦确定了积分形式,均可类比为求解一个不规则立体的体积问题,进而选用上述任一方法进行计算。
三、曲线积分
曲线积分主要分为两类:第一类是对弧长的积分(即第一类曲线积分),第二类是对坐标的积分(即第二类曲线积分)。二者虽在物理意义和表达形式上有所区别,但彼此之间存在可转换的关系。
(1)对弧长的曲线积分——第一类曲线积分
第一类曲线积分的物理背景通常是计算一条曲线的质量,其中f(x, y)表示曲线上各点的线密度。通过对弧长微元ds进行积分,便可得到整条曲线的总质量。由于质量与运动方向无关,因此第一类曲线积分是一个与路径方向无关的量。

观察可知,不论采用何种表达形式,最终都会归结为仅含一个变量的定积分。其余变量只需通过参数化等方式统一转换为该变量的函数即可完成求解。

(2)对坐标的曲线积分——第二类曲线积分
第二类曲线积分常用于描述变力(在x和y方向均有变化)沿曲线路径所做的功。其物理意义即为力在路径上的累积效果。

与第一类类似,第二类曲线积分也可表现为直角坐标形式、参数方程形式或极坐标形式。关键在于将所有变量统一转化为单一参数,从而将其简化为一元定积分问题。
实际应用中,参数方程法最为常用。
(3)两类曲线积分的转换关系
两类曲线积分之间的转换并不复杂,主要依赖于三角函数的基本关系进行推导和理解。





 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







