高等数学第三章 一元函数积分学

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

第一部分：不定积分

1.1 不定积分与原函数的基本概念

原函数：若在某一区间 I 上，存在一个可导函数 F(x)，其导数恰好等于 f(x)，即对于任意 x ∈ I，均有 F’(x) = f(x)，则称 F(x) 是 f(x) 在该区间上的一个原函数。

原函数存在性定理：如果函数 f(x) 在区间 I 上连续，则在该区间上必定存在一个可导函数 F(x)，使得对所有 x ∈ I 都满足 F’(x) = f(x)。这意味着连续函数一定有原函数。

不定积分：在区间 I 上，函数 f(x) 的所有原函数的集合（即带有任意常数项 C 的表达式）称为 f(x) 的不定积分，记作 ∫f(x)dx。

几何意义说明：不定积分对应于一族曲线，这些曲线在横坐标相同的点处具有平行的切线，反映出它们斜率一致的特点。

1.2 常用基本积分公式

• ∫k dx = kx + C （k 为常数）
• ∫x^μ dx = x^μ+1/(μ+1) + C （μ ≠ -1）
• ∫1/x dx = ln|x| + C

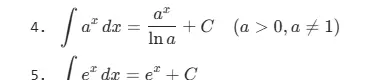
• ∫sin x dx = -cos x + C
• ∫cos x dx = sin x + C
• ∫secx dx = tan x + C
• ∫cscx dx = -cot x + C
• ∫sec x tan x dx = sec x + C
• ∫csc x cot x dx = -csc x + C
• ∫1/(1+x) dx = arctan x + C

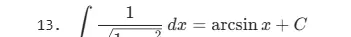
1.3 不定积分的重要性质

线性性质：

• ∫[k·f(x)]dx = k∫f(x)dx （其中 k ≠ 0）
• ∫[f(x)±g(x)]dx = ∫f(x)dx ± ∫g(x)dx

微分与积分之间的关系：

• d[∫f(x)dx] = f(x)dx
• ∫F’(x)dx = F(x) + C

1.4 计算不定积分的主要方法

1.4.1 第一类换元法（凑微分法）

若函数 f(u) 存在原函数 F(u)，且 u = φ(x) 是可导函数，则成立：

∫f[φ(x)]φ’(x)dx = ∫f(u)du = F(u) + C = F[φ(x)] + C

常见的凑微分形式包括：

• ∫f(ax+b)dx = (1/a)∫f(ax+b)d(ax+b)
• ∫f(ln x)(1/x)dx = ∫f(ln x)d(ln x)

+

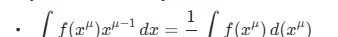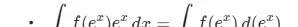
• ∫f(sin x)cos x dx = ∫f(sin x)d(sin x)
• ∫f(tan x)secx dx = ∫f(tan x)d(tan x)

????

例题1：计算 ∫(2x+1)¹⁰ dx

解：令 u = 2x + 1，则 du = 2dx，故 dx = du/2

原式 = (1/2)∫u¹⁰ du = (1/2)·(u¹¹/11) + C = (1/22)(2x+1)¹¹ + C

????

例题2：

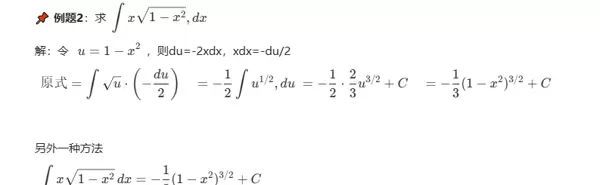
1.4.2 第二类换元法

设 x = φ(t) 是单调且可导的函数，并且 φ’(t) ≠ 0，若复合函数 f[φ(t)]φ’(t) 具有原函数，则有：

∫f(x)dx = ∫f[φ(t)]φ’(t)dt

常用代换方式：

????

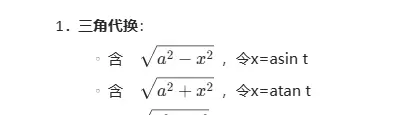例题3：

1.4.3 分部积分法

若 u = u(x) 和 v = v(x) 均具有连续导数，则成立：

∫u dv = uv - ∫v du

选取 u 的优先顺序建议（口诀：反-对-幂-指-三）：

按以下顺序优先选择作为 u：反三角函数 → 对数函数 → 幂函数 → 指数函数 → 三角函数

????

例题4：

????

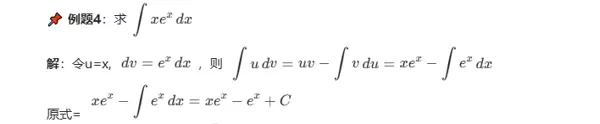例题5：求 ∫x sin x dx

解：令 u = x，dv = sin x dx，则 du = 2x dx，v = -cos x

原式 = -x cos x + 2∫x cos x dx

对 ∫x cos x dx 再次使用分部积分：令 u = x，dv = cos x dx，则 du = dx，v = sin x

∫x cos x dx = x sin x - ∫sin x dx = x sin x + cos x + C

因此，原式 = -x cos x + 2(x sin x + cos x) + C

1.4.4 有理函数的积分处理

有理函数定义：形如 R(x) = P(x)/Q(x)，其中 P(x) 与 Q(x) 均为多项式。

积分步骤：

1. 若为假分式（分子次数 ≥ 分母次数），先通过多项式除法将其化为“多项式 + 真分式”的形式；
2. 将真分式进行部分分式分解；
3. 分别对各个简单分式进行积分。

????

例题6：求 ∫(x+5)/(x5x+6) dx

解：首先对分母因式分解得：x5x+6 = (x2)(x3)

设 (x+5)/[(x2)(x3)] = A/(x2) + B/(x3)

两边通分后得：x+5 = A(x3) + B(x2)

令 x=2 得：7 = A(1) A = 7

令 x=3 得：8 = B(1) B = 8

因此原式 = ∫[7/(x2) + 8/(x3)] dx = 7ln|x2| + 8ln|x3| + C

第二部分：定积分

2.1 定积分的基本概念

定义：设函数 f(x) 在闭区间 [a, b] 上有界，在开区间 (a, b) 内任意插入 n1 个分点，将区间划分为 n 个小区间，构造和式 Σf(ξ_i)Δx_i。当最大小区间长度 λ = max{Δx_i} 趋近于 0 时，若该和式的极限存在且唯一，则称 f(x) 在 [a,b] 上可积，此极限值称为 f(x) 的定积分，记作：

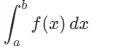
几何意义：表示由曲线 y = f(x)、x 轴以及直线 x=a、x=b 所围成的曲边梯形的面积。

物理意义：可用于描述变速直线运动的路程、变力沿路径所做的功等实际问题。

2.3 可积的条件

函数在某区间上可积需要满足一定的充分条件，主要包括以下两种情况：

• 函数 \( f(x) \) 在闭区间 \([a,b]\) 上连续；
• 函数 \( f(x) \) 在 \([a,b]\) 上有界，且仅有有限个间断点。

2.2 定积分的性质

2.4 牛顿-莱布尼茨公式

若 \( F(x) \) 是连续函数 \( f(x) \) 在区间 \([a,b]\) 上的一个原函数，则有：

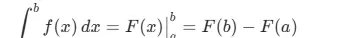
该公式是计算定积分的核心依据，也被称为微积分基本定理。

2.5 定积分的计算方法

2.5.1 换元积分法

设函数 \( f(x) \) 在区间 \([a,b]\) 上连续，变量替换 \( x = \varphi(t) \) 满足以下条件：

• \( \varphi(\alpha) = a, \varphi(\beta) = b \)；
• \( \varphi(t) \) 在区间 \([\alpha,\beta]\) 上具有连续导数，且其值域包含于 \([a,b]\)。

则成立如下换元公式：

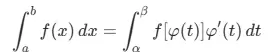
注意：进行变量替换时，积分限必须同步更换，即“换元必换限”。

???? 例题7 ：

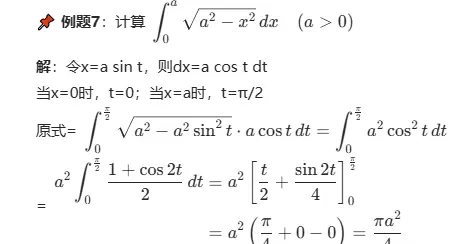
2.5.2 分部积分法

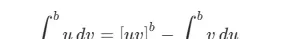
该方法适用于被积函数为两个函数乘积的情形，通过转化简化积分过程。

???? 例题8 ：

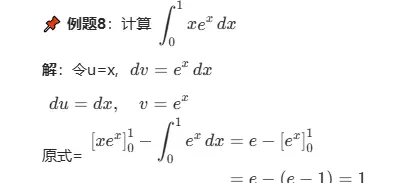
2.6 变上限积分函数及其性质

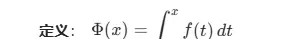
定义变上限积分为：

若 \( f(x) \) 在 \([a,b]\) 上连续，则函数 \( \Phi(x) \) 在 \([a,b]\) 上可导，且导数为 \( \Phi'(x) = f(x) \)。

进一步地，\( \Phi(x) \) 是 \( f(x) \) 在该区间上的一个原函数。

???? 例题9 ：

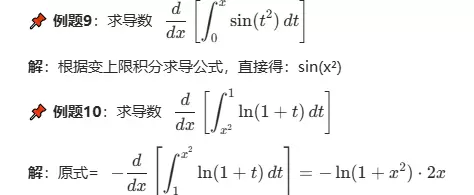
2.7 广义积分

2.7.1 无穷限的广义积分

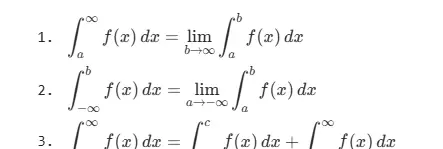
对于积分区间为无穷的情况，需讨论其收敛性。常用的判别方法包括：

• 比较判别法：通过与已知收敛或发散的非负函数比较；
• 极限判别法：利用极限形式判断趋近行为；
• 绝对收敛性：若 \( \int |f(x)| \, dx \) 收敛，则 \( \int f(x) \, dx \) 也收敛。

???? 例题11 ：

2.7.2 无界函数的广义积分（瑕积分）

若函数 \( f(x) \) 在某点 \( a \) 的任意邻域内无界，则称点 \( a \) 为 \( f(x) \) 的瑕点。此类积分需在去除奇点后取极限处理。

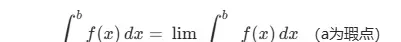
???? 例题12 ：

2.8 定积分在几何学中的应用

2.8.1 平面图形的面积

2.8.2 体积

*：

2.9 定积分在物理学中的应用

???? 总结

模块	重点内容	常见考点
不定积分	基本公式、换元法、分部积分法、有理函数积分	凑微分、三角代换、分部积分的选取
定积分	性质、N-L公式、换元法、分部积分法	对称区间积分、周期函数积分、含绝对值积分
变上限积分	求导、相关极限	与导数定义结合
广义积分	无穷限积分、瑕积分	收敛性判断、计算
积分应用	面积、体积、弧长、物理应用	几何应用为主

本章作为微积分的重要组成部分，要求熟练掌握各类积分技巧，深入理解定积分的概念与基本性质，并能够灵活运用于解决几何与物理中的实际问题。

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：高等数学 一元函数 Alpha 不定积分 广义积分