发帖
雷达卡
一、目标函数的构建
在完成模型结构的设计之后，下一步是让模型具备完成特定任务的能力，这一过程被称为“模型训练”。训练的核心在于通过调整模型内部的参数，使得其预测结果逐步逼近真实情况。
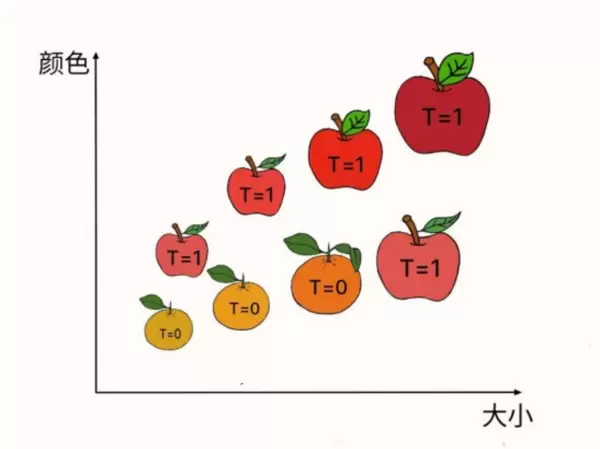
以苹果与桔子的分类任务为例，可以设计一个简单的线性模型来实现区分：
Y = A × 颜色 + B × 大小 + C
其中，A、B 和 C 是待学习的模型参数，它们共同决定了模型的行为方式（如图 12.4 中所示的蓝色分类平面）。训练的目的就是基于已有数据，找到一组最优的参数值，使模型能够更精确地进行判断。
为了实现这一目标，首先需要收集一批苹果和桔子的实际样本，构成一个“训练集”。在该数据集中，使用变量 T 表示每个样本的真实类别：若为苹果，则标记为 T=1；若为桔子，则标记为 T=0。
接下来的关键步骤是定义一个“损失函数”，用于量化模型预测输出 Y 与真实标签 T 之间的偏差。例如，可采用如下形式的损失函数 L：
L = (Y - T)
这里，Y 代表模型的预测值，T 为实际类别标签。损失函数的数值越小，说明预测结果越接近真实值，模型表现也就越好。因此，整个训练过程可以被转化为一个数学优化问题：寻找一组参数（A, B, C），使得损失函数 L 的取值尽可能小。
二、优化策略对比：随机尝试法与梯度下降法
在定义好损失函数后，模型训练的关键转变为如何有效地最小化该函数。这个过程本质上属于数学中的优化范畴，研究者提出了多种不同的优化算法，各自具有不同的特点和适用场景。
一种直观的方法是“随机尝试法”，其过程如图示。首先对参数 A、B、C 赋予一组随机初始值，然后在其邻域内不断生成新的参数组合。如果新组合导致损失函数 L 下降，则接受该更新；否则继续尝试其他组合。经过多次迭代后，如图（A）至（D）所示，L 值逐渐减小，对应的苹果与桔子的分类边界也日趋精准。
这种方法的优势在于通用性强——只要能计算出损失函数值，就可以应用此策略，不受模型或任务类型的限制。然而，其主要缺点是效率低下，因为缺乏方向性指导，完全依赖随机探索，收敛速度慢。
为了提升优化效率，通常会引入损失函数的几何特性作为指引。其中，“梯度下降法”因其简洁高效而成为主流选择。
梯度下降法的思想类似于一个人从山顶向山谷下行的过程：假设某人站在山坡上，希望尽快到达最低点。他会采取以下步骤：
- 观察周围地形，找出当前最陡峭的下坡方向；
- 沿着该方向迈出一步；
- 重复上述过程，直到无法再显著降低高度为止。
类比到机器学习中，将模型参数视作空间坐标，损失函数的输出值则对应“海拔高度”，整个函数形成一个高维曲面（见图 12.8）。梯度下降法从某个初始点 A（损失较高）出发，在每一步都计算损失函数在该点的梯度（即局部变化最快的方向），并沿梯度的反方向移动一小步，从而逐步逼近极小值点 C。由于梯度指示了上升最快的方向，因此其反方向即为下降最快的方向。
应用于苹果-桔子分类模型时，具体流程如下：
- 随机初始化参数 A、B、C；
- 计算当前损失函数关于各参数的梯度；
- 按照梯度反方向更新参数；
- 重复执行直至损失函数趋于稳定，不再明显下降。
目前，梯度下降法是机器学习领域中最广泛使用的优化手段之一。相比图中展示的随机尝试方法，它利用了损失函数的局部导数信息，显著提高了搜索效率。同时，相较于一些更为复杂的高级优化算法，梯度下降法结构简单、易于实现，尤其适用于大规模数据集下的训练任务。
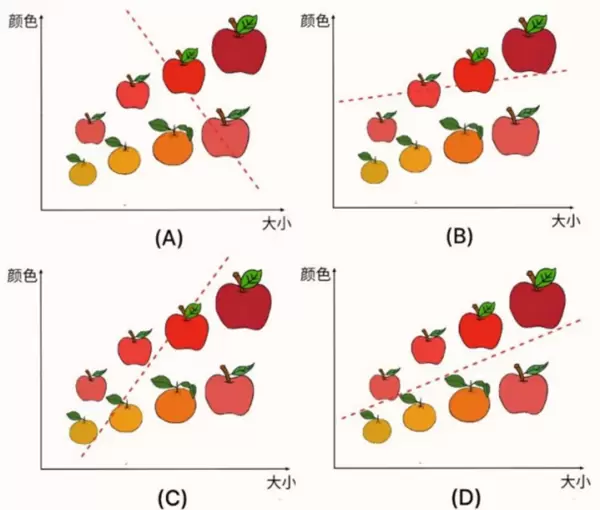
训练过程中分类面的演化过程
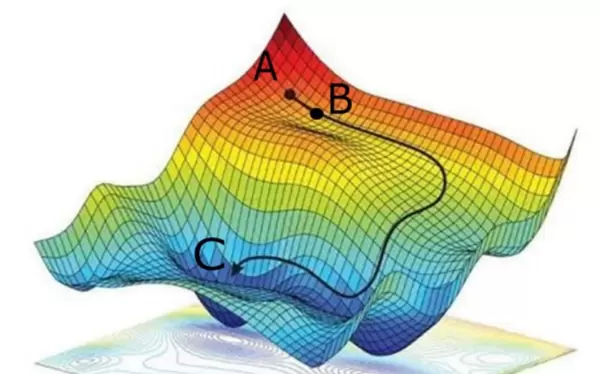
梯度下降法原理示意图
京公网安备 11010802022788号
