Matlab中基于Music算法的时序信号频率估计方法
在信号处理领域,频率估计是一项至关重要的任务,尤其在电力系统、通信和故障诊断等实际场景中具有广泛应用。本文将详细介绍如何利用Music(Multiple Signal Classification)算法在Matlab中实现高精度的时序信号频率估计,并探讨其在谐波检测与突变识别中的潜力。
该方法不仅适用于复杂背景噪声下的频率提取,还可作为其他频率估计算法性能对比的基准工具,在工程实践中展现出显著优势。
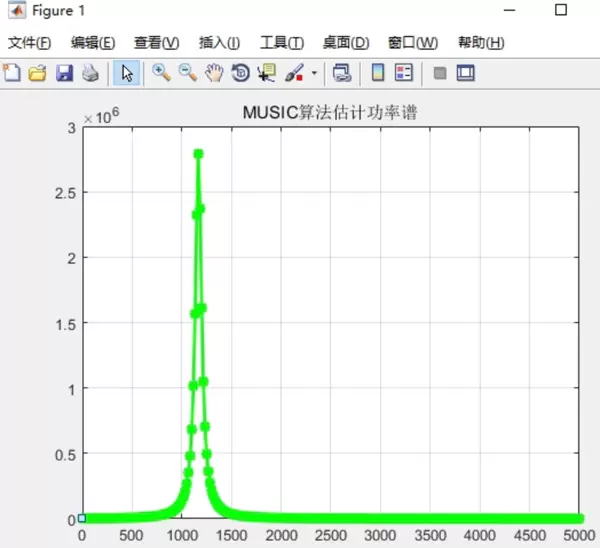
Music算法的核心原理
Music算法全称为“多重信号分类”算法,其核心思想是利用信号子空间与噪声子空间之间的正交特性来实现频率参数的精确估计。假设待分析的时序信号由多个复正弦成分叠加而成,其数学模型可表示为:
\[ x(n) = \sum_{i=1}^{p} a_i e^{j2\pi f_i n} + w(n) \]其中,\( p \) 表示信号源数量,\( a_i \) 为第 \( i \) 个信号的幅度,\( f_i \) 是对应频率,而 \( w(n) \) 代表加性噪声。通过对观测信号构建协方差矩阵并进行特征值分解,可以将其对应的特征向量划分为两个相互正交的子空间:包含主要能量信息的信号子空间和以噪声为主的噪声子空间。
随后,通过构造Music谱函数,寻找其峰值位置,即可准确估计出原始信号中的各个频率分量。由于该方法不依赖于传统的傅里叶变换框架,因此具备更高的分辨率和更强的抗噪能力。
Matlab实现流程详解
信号建模与参数设定
首先设置采样频率 \( fs \) 和时间序列 \( t \),并定义两个或多个不同频率的正弦信号(如 \( f1 \) 和 \( f2 \)),合成一个多频混合信号 \( x \)。这一过程相当于构建一个可控的测试环境,便于后续验证算法的有效性。
自相关与协方差矩阵构建
使用Matlab中的 xcorr 函数计算信号的自相关序列,并据此构造归一化的协方差矩阵 \( Rx \)。此矩阵蕴含了信号内部各成分的相关结构信息,是后续子空间划分的基础数据。
特征值分解与排序
对协方差矩阵 \( Rx \) 进行特征分解,得到特征值矩阵 \( D \) 与对应的特征向量矩阵 \( V \)。接着按照特征值从大到小的顺序重新排列,确保能量最强的成分位于前端,从而为正确划分子空间提供保障。
信号与噪声子空间分离
根据已知或预估的信号源数目 \( p \),将前 \( p \) 个最大特征值对应的特征向量归入信号子空间 \( Es \),其余则构成噪声子空间 \( En \)。这种划分充分利用了信号与噪声在统计特性上的差异,是Music算法实现高分辨估计的关键步骤。
Music谱生成与频率提取
在设定的频率范围内,逐点计算Music谱值 \( Pmusic \),其计算依据是噪声子空间与信号导向矢量之间的正交关系。当测试频率接近真实信号频率时,导向矢量与噪声子空间正交程度最高,导致谱值出现明显峰值。
最终绘制出的Music谱图能够清晰显示所有估计频率的位置,实现直观且精准的频率识别。
% 参数设置
fs = 1000; % 采样频率
t = 0:1/fs:1 - 1/fs; % 时间向量
f1 = 50; f2 = 120; % 两个正弦信号频率
x = 2*cos(2*pi*f1*t) + 3*cos(2*pi*f2*t); % 合成信号
N = length(x); % 信号长度
% 计算协方差矩阵
Rxx = xcorr(x)/N;
Rx = toeplitz(Rxx(1:N));
% 特征分解
[V,D] = eig(Rx);
eigenvalues = diag(D);
[eigenvalues_sorted,index] = sort(eigenvalues,'descend');
V = V(:,index);
% 信号和噪声子空间划分
p = 2; % 信号源个数
Es = V(:,1:p); % 信号子空间
En = V(:,(p + 1):end); % 噪声子空间
% Music谱计算
f = 0:0.01:fs/2;
Pmusic = zeros(size(f));
for i = 1:length(f)
a = exp(-j*2*pi*f(i)*(0:N - 1)');
Pmusic(i) = 1/(a'*En*En'*a);
end
% 绘图
figure;
plot(f,10*log10(Pmusic/max(Pmusic)));
xlabel('Frequency (Hz)');
ylabel('Magnitude (dB)');
title('MUSIC Spectrum');
grid on;在电力系统中的典型应用
谐波成分检测
电力系统中常因非线性负载引入多种谐波成分,影响电能质量并可能损坏设备。基于Music算法的频率估计算法能够高效识别出这些隐藏在主频周围的谐波频率,即使在低信噪比条件下也能保持良好性能。它如同一位精准的“频谱猎手”,快速定位各类谐波干扰源,助力工程师制定有效的治理策略。
运行状态突变监测
当电网发生短路、断线或其他异常事件时,电压或电流信号的频率往往会出现瞬时偏移。Music算法凭借其对频率动态变化的高度敏感性,能够在突变发生的第一时间捕捉到频率波动,进而触发保护机制,提升系统安全性和稳定性。
与其他频率估计算法的比较优势
相较于传统周期图法,Music算法在低信噪比环境下表现出更优的鲁棒性和分辨率。虽然周期图法实现简单,但易受旁瓣泄漏和噪声干扰影响,难以区分邻近频率成分。而Music算法通过子空间建模有效抑制噪声干扰,显著提升了估计精度。
与Capon算法相比,Music算法在多信号源共存的情况下具备更强的频率分辨能力,能够更清晰地区分彼此接近的不同频率信号,且计算稳定性更高,更适合用于复杂电力信号的分析任务。
总结
综上所述,基于Music算法的时序信号频率估计方法在Matlab平台中具备良好的可实现性与实用性。无论是在理论研究层面,还是在电力系统的谐波检测、故障预警等实际工程应用中,均展现出强大的分析能力和广阔的应用前景。掌握该技术有助于提升信号处理项目的整体性能,值得深入学习与推广。




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







