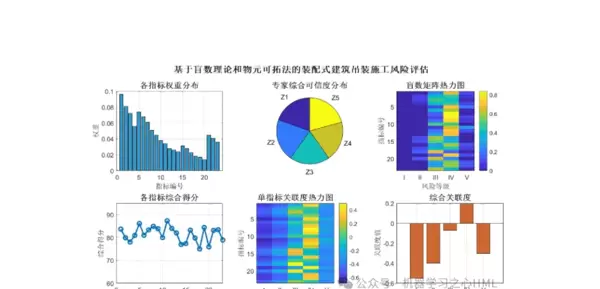
模型核心理念
本模型的设计基于两大理论支柱:盲数理论与物元可拓法,旨在更科学地应对装配式建筑吊装过程中存在的不确定性与模糊性。
盲数处理不确定性信息:在实际施工中,许多风险因素(如人员经验水平、设备运行状态、风速变化等)难以用精确数值描述。这些信息往往具有主观性和不完整性。盲数理论通过引入“取值区间+可信度分布”的表达方式,能够有效刻画专家判断中的模糊性与不确定性,从而实现对定性信息的量化处理。
物元可拓实现等级划分:传统的风险分级方法通常依赖硬性阈值,难以反映现实中的过渡状态。而物元可拓法通过构建标准物元与待评物元之间的关联关系,利用关联度计算来判断风险所属等级,尤其适用于边界不清、存在“亦此亦彼”特征的评判场景。
模型构建流程
第一步:构建风险评估指标体系
系统识别影响装配式建筑吊装安全的关键因素,并建立分层结构的评估框架:
- 目标层(A):装配式建筑吊装施工综合风险评估结果。
- 准则层(B):从六个维度展开,包括:
- B1:人员因素
- B2:机械设备因素
- B3:构件与材料因素
- B4:技术工艺因素
- B5:环境因素
- B6:管理因素
- 指标层(C):进一步细化至具体可操作的评估项,例如:
- C11:指挥司索工技能与经验
- C12:吊装工人安全意识
- C21:塔吊或汽车吊的工作性能与现状
- C22:吊索具的完好程度
- C51:天气状况(如风速、雨雪情况)
- C52:作业区域的空间复杂性
第二步:确定各指标权重
采用层次分析法(AHP)或熵权法等方法,计算不同层级指标的相对重要性权重向量 $W$。为增强对不确定性的表达能力,可邀请多位专家以盲数形式进行两两比较判断。
盲数判断示例:某专家认为指标i相对于指标j“略为重要”,但把握不大,于是给出区间判断“介于2到4之间”,并附加可信度分布——“2~3的可能性为40%,3~4的可能性为60%”。这一判断即可转化为一个盲数形式,用于后续运算。
第三步:设定风险等级的标准物元
将施工风险划分为若干等级,如:
- Ⅰ级:低风险
- Ⅱ级:一般风险
- Ⅲ级:较高风险
- Ⅳ级:高风险
针对每个底层指标 $C_i$,定义其在各风险等级下的合理取值范围,进而构建以下两类物元矩阵:
经典域物元 $R_j$ 表示第 $j$ 级风险下各指标的标准范围:
$$ R_j = (N_j, C_i, V_{ji}) = \begin{bmatrix} N_j & C_1 & (a_{j1}, b_{j1}) \\ & C_2 & (a_{j2}, b_{j2}) \\ & \vdots & \vdots \\ & C_n & (a_{jn}, b_{jn}) \end{bmatrix} $$其中,$N_j$ 代表第 $j$ 风险等级,$(a_{ji}, b_{ji})$ 是指标 $C_i$ 在该等级下的数值区间。
节域物元 $R_P$ 描述所有等级中指标 $C_i$ 的总体可能范围:
$$ R_P = (P, C_i, V_{Pi}) = \begin{bmatrix} P & C_1 & (a_{P1}, b_{P1}) \\ & C_2 & (a_{P2}, b_{P2}) \\ & \vdots & \vdots \\ & C_n & (a_{Pn}, b_{Pn}) \end{bmatrix} $$其中,$P$ 表示全部风险等级集合,$(a_{Pi}, b_{Pi})$ 为指标 $C_i$ 的全局取值区间。
第四步:获取待评估物元(融合盲数)
这是模型的核心创新环节。组织多位专家对当前项目中各项底层指标 $C_i$ 的风险状况进行评估。由于认知局限和信息缺失,专家不再提供单一数值,而是采用盲数形式表达判断。
专家评估实例:对于指标 $C_i$,专家 $k$ 可能表示:“我认为风险值在60至80之间,其中60~70的概率占30%,70~80的概率占70%。”
该判断被形式化为一个盲数 $\tilde{x}_i^k$。随后,将 $m$ 位专家对同一指标的盲数评估进行加权整合,得到最终的综合盲数评估值 $\tilde{x}_i$。
由此形成的待评物元 $R$ 如下所示:
$$ R = \begin{bmatrix} P & C_1 & \tilde{x}_1 \\ & C_2 & \tilde{x}_2 \\ & \vdots & \vdots \\ & C_n & \tilde{x}_n \end{bmatrix} $$第五步:计算盲数关联度
计算待评物元 $R$ 相对于各个风险等级 $N_j$ 的盲数关联度 $K_j(\tilde{x}_i)$,以判定整体风险归属。
首先,针对每一个指标 $C_i$,利用盲数距离公式,计算其盲数 $\tilde{x}_i$ 与各等级 $j$ 之间的关联程度。该过程依托于物元可拓理论中的“距”概念,通过数学建模实现从模糊输入到清晰等级输出的转化。
在风险评估模型中,针对指标 $C_i$ 属于等级 $j$ 的可信度分布,定义盲数关联度函数如下:
\[ K_j(x) = \begin{cases} \frac{-\rho(x, V_{ji})}{|V_{ji}|} & x \in V_{ji} \\ \frac{\rho(x, V_{ji})}{\rho(x, V_{Pi}) - \rho(x, V_{ji})} & x \notin V_{ji} \end{cases} \]由于输入变量 $x$ 实际为盲数 $\tilde{x}_i$,因此在计算 $\rho(\tilde{x}_i, V_{ji})$ 与 $\rho(\tilde{x}_i, V_{Pi})$ 时需依据盲数运算规则进行处理。最终所得的 $K_j(\tilde{x}_i)$ 同样表现为一个盲数,用以描述该指标归属于某一风险等级的不确定性程度。
综合风险等级判定流程
1. 综合关联度计算
将各单项指标的盲数关联度 $K_j(\tilde{x}_i)$ 按其权重 $w_i$ 进行加权融合,得到项目相对于第 $j$ 风险等级的综合盲数关联度 $\tilde{K}_j$,表达式为:
\[ \tilde{K}_j = \sum_{i=1}^{n} w_i \cdot K_j(\tilde{x}_i) \]2. 盲数清晰化处理
对综合盲数 $\tilde{K}_j$ 应用清晰化方法(例如求其期望值 $E[\tilde{K}_j]$),将其转化为确定性数值 $K_j$,便于后续比较和决策。
3. 风险等级判定准则
采用最大关联度原则进行等级划分:若存在某个 $j0$ 使得 $K_{j0} = \max_{j \in \{1,2,3,4\}} K_j$,则判定该项目的综合风险等级为 $j0$。

模型核心优势分析
- 信息利用充分性:盲数理论能够有效整合专家判断中存在的区间信息与主观不确定性,避免传统方法因强行精确化而导致的信息失真问题。
- 评估结果更精确:物元可拓法通过构建定量化的关联函数,使评估结果比普通模糊综合评判更具分辨力,能准确反映实际状态与标准等级之间的“贴近程度”。
- 动态适应能力强:当施工现场条件发生变化时,仅需更新待评物元中的盲数参数,即可快速完成新一轮风险评估,具备良好的实用性与时效性。
- 系统性结构完整:该模型实现了定性与定量、主观经验与客观数据的有效融合,形成了一套逻辑严密、流程清晰的风险评估体系。
应用实例:PC项目吊装施工“环境因素(B5)”风险评估
评估对象与指标设置
选取“环境因素”作为评估维度,包含以下两个子指标:
- C51:风速
- C52:作业空间
对应权重向量为 $W = (0.6, 0.4)$。
风险等级划分(以C51为例)
设定四个风险等级,经典域范围如下:
- Ⅰ级:(0, 10) km/h
- Ⅱ级:(10, 20) km/h
- Ⅲ级:(20, 30) km/h
- Ⅳ级:(30, 50) km/h
专家盲数评估结果
结合多位专家意见,获得如下盲数表达:
- C51(风速):$\tilde{x}_1 =$ {[15,20], 0.7; [20,25], 0.3} —— 表示风速处于15–20区间的可能性为70%,20–25为30%。
- C52(作业空间):$\tilde{x}_2 =$ {[60,70], 0.4; [70,80], 0.6}
关联度计算与合成
分别计算 $\tilde{x}_1$ 和 $\tilde{x}_2$ 对应四个等级的盲数关联度 $K_j(\tilde{x}_i)$,并通过加权合成得出综合盲数关联度 $\tilde{K}_j$。经清晰化处理后,获得如下确定值:
\[ K_1 = -0.52,\quad K_2 = 0.15,\quad K_3 = -0.21,\quad K_4 = -0.65 \]评估结论
根据最大关联度原则,$\max K_j = K_2 = 0.15$,故判定“环境因素”的综合风险等级为Ⅱ级(一般风险)。
[此处为图片3]总结
基于盲数理论与物元可拓法构建的装配式建筑吊装施工风险评估模型,成功应对了评估过程中普遍存在的模糊性与不确定性挑战,提供了一条科学、严谨且可操作性强的风险量化路径。该方法不仅适用于吊装环节的风险识别,经过适当调整后还可拓展至装配式建筑全生命周期内的其他关键阶段,具有显著的理论研究价值与广泛的工程应用前景。




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







