在电力电子技术的发展进程中,单相模块化多电平换流器(MMC)整流器因其出色的波形质量与可扩展性结构而受到广泛关注。然而,在实际运行中,该系统面临诸如环流抑制、子模块电压均衡等关键技术难题。与此同时,载波移相调制作为一种核心调制策略,在提升系统性能方面发挥着不可替代的作用。本文将围绕这些关键问题展开分析。
单相MMC整流器的基本结构与工作原理
单相MMC整流器通常由多个子模块(SM)在直流侧串联构成,每个子模块可采用半桥或全桥拓扑结构。交流侧连接至电网,通过精确控制各子模块的投切状态,能够合成接近理想正弦波的输出电压,从而显著降低谐波畸变率。这种模块化设计不仅提高了系统的灵活性和可靠性,也便于实现高压大功率应用。
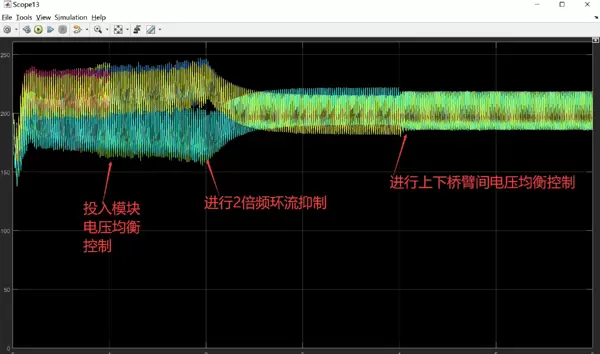
环流的产生与抑制方法
在单相MMC系统中,环流是影响效率与稳定性的主要因素之一。它主要包括零序和负序分量,容易引起额外损耗、温升加剧甚至设备损坏。因此,有效抑制环流至关重要。
一种常用的解决方案是引入比例谐振(PR)控制器。该控制器能够在特定频率下提供高增益,从而精准跟踪并抑制周期性干扰信号,如三次谐波为主的环流成分。
以下为一段示意性Python代码,展示PR控制器的基本实现逻辑(仅用于说明算法流程,实际工程需结合实时控制系统与专业库函数):
import numpy as np
import matplotlib.pyplot as plt
# 定义参数
omega = 2 * np.pi * 50 # 电网角频率
kp = 0.5 # PR控制器比例系数
kr = 10 # PR控制器谐振系数
# 模拟环流信号
time = np.linspace(0, 0.1, 1000)
circulating_current = np.sin(omega * time) + 0.5 * np.sin(3 * omega * time)
# PR控制器
def pr_controller(error, omega):
integral = 0
output = 0
for e in error:
integral += e * 0.0001 # 简单积分近似
output = kp * e + kr * integral * np.cos(omega * 0.0001)
yield output
error = -circulating_current # 假设这里是测量得到的环流与目标值(0)的误差
pr_output = list(pr_controller(error, omega))
# 绘制结果
plt.figure(figsize=(10, 6))
plt.plot(time, circulating_current, label='Circulating Current')
plt.plot(time, pr_output, label='PR Controller Output')
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.legend()
plt.grid(True)
plt.show()代码中设定了电网角频率、PR控制器的比例系数
kp以及谐振增益参数
kr,并模拟了一个包含基波与三次谐波的环流输入信号。通过
pr_controller函数对误差进行处理,生成相应的控制输出。仿真结果图显示,经过PR调节后,环流幅值得到明显衰减,验证了其理论有效性。
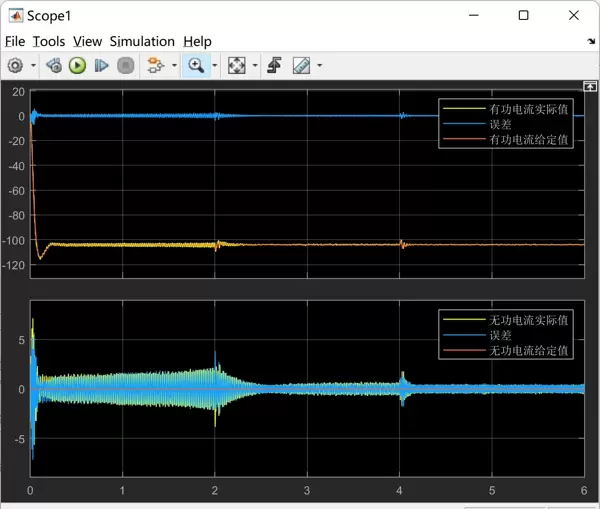
电压均衡控制策略
由于制造差异、老化程度不一或控制延迟等因素,各个子模块中的电容电压可能出现不平衡现象,进而影响整体系统稳定性。为此,必须实施有效的电压均衡机制。
排序法是一种广泛应用的均衡控制手段。其实现方式为:实时采集所有子模块的电容电压值,并按大小排序;根据当前所需投入的模块数量,优先选择电压较低者投入运行,或对电压过高者进行放电操作,从而逐步实现电压一致性。
以下是该过程的简化伪代码描述:
// 假设submodule_voltages是存储各子模块电压的数组
// num_submodules是子模块数量
for (int i = 0; i < num_submodules; i++) {
for (int j = i + 1; j < num_submodules; j++) {
if (submodule_voltages[i] > submodule_voltages[j]) {
// 交换电压值
float temp = submodule_voltages[i];
submodule_voltages[i] = submodule_voltages[j];
submodule_voltages[j] = temp;
}
}
}
// 根据排序结果进行子模块的开通关断决策,这里省略具体逻辑在具体应用中,该策略常与最近电平逼近(NLM)或其他调制方式协同使用,动态调整子模块的通断顺序,确保在满足输出要求的同时维持电压均衡。
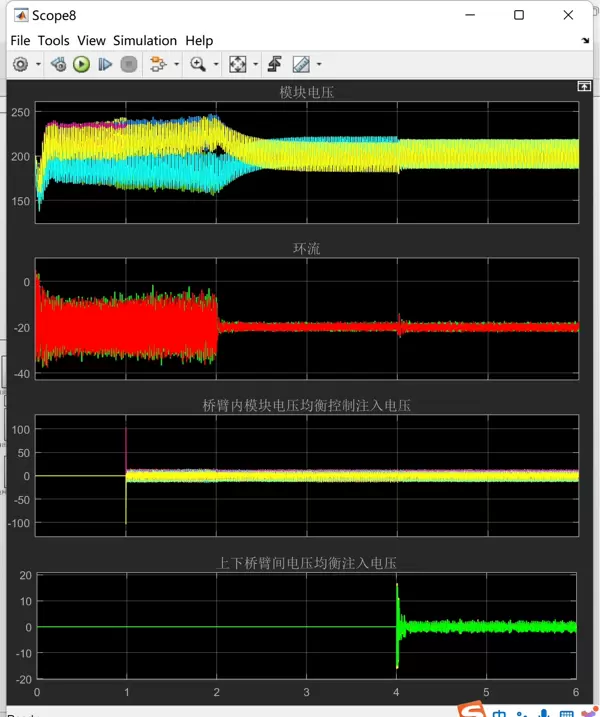
载波移相调制的技术优势与实现
载波移相调制(Phase-Shifted Carrier Modulation, PSCM)是单相MMC中常用的脉宽调制技术。其核心思想是为每个子模块分配一个相位依次偏移的三角载波,所有载波频率相同但相位差为 $2\pi / N$(N为子模块总数),然后将统一的调制波与各载波比较,生成独立的驱动信号。
这种方式能显著提高系统的等效开关频率,减小输出电压的谐波含量,同时避免集中式调制带来的局部过热问题。
下面是一段MATLAB代码示例,用于演示PSCM的实现过程:
N = 5; % 子模块数量
fs = 1000; % 采样频率
t = 0:1/fs:0.1; % 时间向量
modulation_signal = sin(2*pi*50*t); % 调制信号
carriers = zeros(N, length(t));
for k = 1:N
carriers(k, :) = sin(2*pi*fs/N*t + (k - 1)*2*pi/N);
end
gates = zeros(N, length(t));
for k = 1:N
gates(k, :) = modulation_signal > carriers(k, :);
end
figure;
subplot(N + 1, 1, 1);
plot(t, modulation_signal);
title('Modulation Signal');
xlabel('Time (s)');
ylabel('Amplitude');
for k = 1:N
subplot(N + 1, 1, k + 1);
plot(t, carriers(k, :));
hold on;
plot(t, gates(k, :)*1.5, 'r--');
title(['Carrier and Gate Signal for SM', num2str(k)]);
xlabel('Time (s)');
ylabel('Amplitude');
hold off;
end程序首先设定子模块数量
N、采样频率
fs等基础参数,随后构建调制波与多个相位偏移的载波信号,并通过比较生成各子模块的触发脉冲序列(
gates)。从输出图形可以清晰观察到不同载波之间的相位错位关系及其对应的脉冲分布,直观展现了PSCM的工作特性。
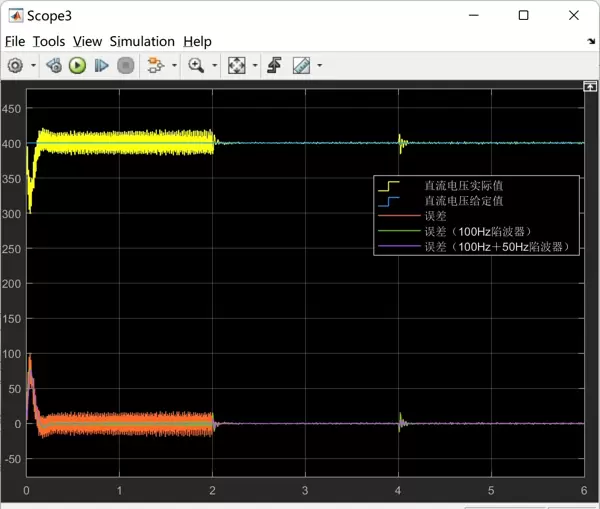
总结与展望
综上所述,单相MMC整流器的高性能运行依赖于环流的有效抑制、子模块电压的动态均衡以及先进调制策略的应用。这三项技术相互支撑、协同作用,共同保障系统在复杂工况下的稳定性与效率。
载波移相调制提升了输出波形品质,PR控制增强了对特定谐波特性的响应能力,而排序法则保证了能量存储单元的长期可靠运行。未来,随着数字控制技术与智能算法的发展,这些控制策略仍有广阔的优化空间,有望进一步推动电力电子系统向更高效率、更智能化方向演进。




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







