一、核心功能概述
本方案构建了一套完整的随机森林回归建模与优化流程,基于 MATLAB 平台实现。主要涵盖以下环节:
- 数据预处理及训练集/测试集划分
- 结合网格搜索与交叉验证的超参数调优
- 最优参数下的模型训练与性能评估
- 采用 SHAP 方法进行特征贡献度解析
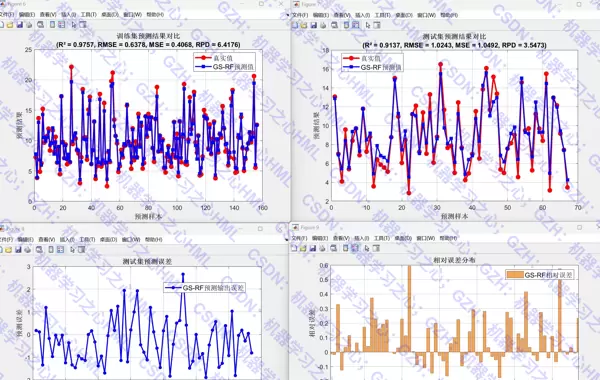
- 多维度结果可视化:包括参数搜索空间展示、误差分析图、拟合效果对比、特征重要性排序等
二、技术实现步骤
1. 数据准备阶段
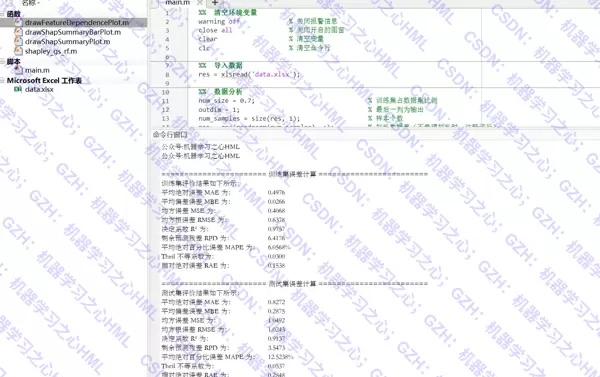
从 Excel 文件(.xlsx 格式)中加载原始数据,确保最后一列为待预测的目标变量。随后对样本顺序进行随机打乱,避免潜在的排序偏差影响模型训练。
按照 7:3 的比例将数据划分为训练集和测试集,并使用 mapminmax 方法对输入特征进行归一化处理,以提升模型收敛稳定性。
2. 参数优化策略
采用网格搜索(Grid Search)结合 5 折交叉验证的方式,系统性地探索关键超参数组合的性能表现。
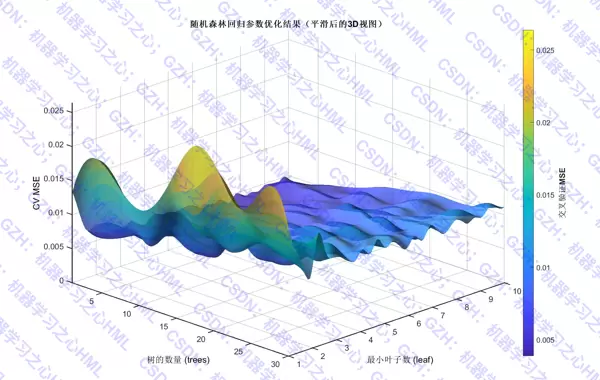
遍历决策树数量(从1到30)与最小叶子节点样本数(从1到10)构成的参数空间,针对每组配置计算其在交叉验证过程中的平均均方误差(MSE),用于衡量泛化能力。
trees = 1:30leaf = 1:103. 模型训练与评估
选定最优参数后,利用 TreeBagger 函数训练最终的随机森林回归模型。同时记录袋外误差(OOB Error),作为模型稳定性的内部评估指标。
模型输出特征重要性评分,并对训练集与测试集分别进行预测。预测值经过反归一化还原至原始量纲,便于后续解释。
评估阶段计算多个性能指标:决定系数 R、均方根误差 RMSE、平均绝对误差 MAE、平均绝对百分比误差 MAPE、RPD 以及 Theil 不一致性系数。
4. 可解释性分析 —— SHAP 值计算
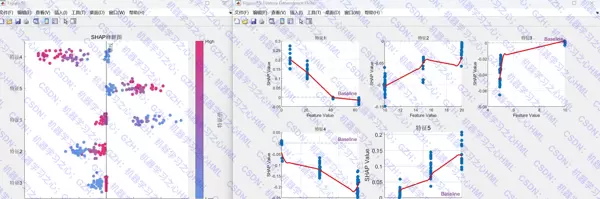
引入 SHAP(Shapley Additive exPlanations)方法,量化各输入特征对每个样本预测结果的边际贡献。
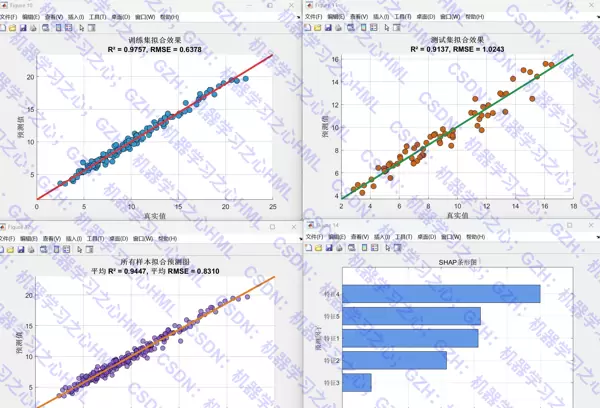
生成 SHAP 摘要图与特征依赖图,直观揭示特征与模型输出之间的非线性关系及方向性影响。
5. 多样化结果可视化
输出多种图形化报告,包括:
- 参数搜索三维曲面图,展示不同参数组合下的误差分布
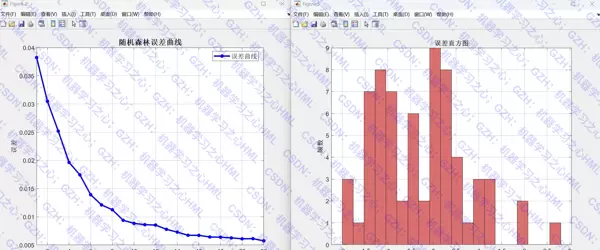
- 训练误差随树数量变化的趋势曲线
- 实际值 vs 预测值的拟合图与散点图
- 残差直方图,反映误差分布形态
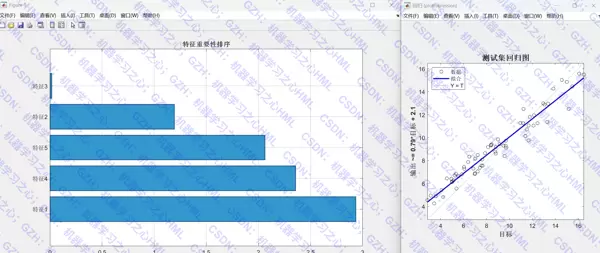
- 特征重要性条形图,突出关键影响因子
- 线性拟合评估图,辅助判断模型精度
三、整体技术路线
本方法的技术架构如下:
- 基础模型:采用 MATLAB 内置的 TreeBagger 实现随机森林回归
- 优化机制:通过网格搜索配合 5 折交叉验证寻找最佳参数组合
- 解释工具:集成 SHAP 算法增强模型可解释性
- 评价体系:综合 R、RMSE、MAE、MAPE、RPD 和 Theil 系数等多维指标全面评估模型表现
数据导入 → 预处理 → 网格搜索+CV → 训练模型 → 预测 → 评估 → SHAP解释四、核心公式与理论依据
1. 随机森林回归原理
该模型由多个决策树集成而成,最终输出为所有树预测结果的平均值。每棵树在训练时仅使用部分样本和特征,提升模型多样性与抗过拟合能力。
袋外误差(OOB Error)利用未参与某棵树训练的样本进行内部验证,提供无需额外验证集的模型性能估计。
2. 主要评估指标定义
均方根误差 RMSE:
RMSE = √(1/N × Σ(y_i - _i))
决定系数 R:
R = 1 - [Σ(y_i - _i) / Σ(y_i - )]
平均绝对百分比误差 MAPE:
MAPE = (100% / N) × Σ| (y_i - _i) / y_i |
Theil 不一致性系数 U:
U = √[ (1/N) × Σ(y_i - _i) ] / { √[ (1/N) × Σy_i ] + √[ (1/N) × Σ_i ] }
3. SHAP 值计算原理
SHAP 值源于合作博弈论中的 Shapley 值概念,用于公平分配每个特征对预测结果的贡献。
对于第 i 个特征,其 SHAP 值 φ_i 定义为所有可能特征子集 S(不包含 i)下,加入该特征前后模型输出变化的加权平均:
φ_i = Σ_{S F \ {i}} [ |S|!(|F||S|1)! / |F|! ] × [ f(S ∪ {i}) f(S) ]
五、关键参数设置
| 参数名称 | 取值或范围 | 说明 |
|---|---|---|
| 训练集占比 | 0.7 | 数据集中70%用于训练,其余用于测试 |
| 决策树数量搜索范围 | 1:30 | 尝试从1到30棵决策树的不同组合 |
| 最小叶子样本数搜索范围 | 1:10 | 控制每棵决策树的复杂度与过拟合风险 |
| 交叉验证折数 | 5 | 采用5折交叉验证评估参数性能 |
| 任务类型 | 'regression' | 指定为回归任务模式 |
num_sizetrees_rangeleaf_rangekMethod六、运行环境要求
- 软件平台:MATLAB R2018b 或更高版本
- 必需工具箱:Statistics and Machine Learning Toolbox
- 可选支持:需自行导入或实现 SHAP 分析相关函数
- 输入数据格式:Excel 文件(.xlsx),最后一列应为目标输出变量
七、典型应用领域
该方法适用于各类连续型变量的回归预测问题,尤其适合以下场景:
- 房价趋势预测
- 商品销量或市场需求建模
- 工业生产过程中关键参数的动态估计
- 环境因素对生态指标的影响分析
- 金融风险等级或违约概率评估
特别推荐应用于:
- 中小规模数据集(数百至数千样本)
- 特征之间存在显著非线性交互关系的情况
- 需要高可解释性支持决策分析的任务




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







