Lecture 2:马尔科夫决策过程(Markov Decision Process)
本节课将围绕“马尔科夫决策过程”展开。在上一讲中,我们了解了强化学习智能体(agent)的基本构成,主要包括模型(model)、价值函数(value)和策略(policy)三个部分。本节将进一步深入,介绍强化学习的核心数学框架——马尔科夫决策过程(MDP)。
为了更好地理解MDP,我们将从其简化形式入手,依次讲解马尔科夫链(Markov Chain)和马尔科夫奖励过程(Markov Reward Process)。通过逐步递进的方式,帮助大家更清晰地掌握MDP的本质。随后,课程还将涵盖策略评估(policy evaluation)以及MDP中的控制问题,重点介绍两种经典算法:策略迭代(policy iteration)和价值迭代(value iteration)。

一、从马尔科夫链到马尔科夫决策过程
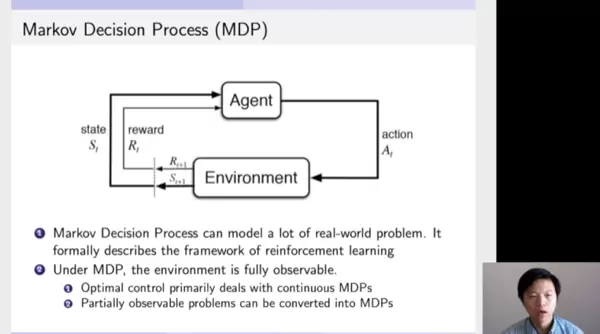
该部分展示了强化学习中智能体(Agent)与环境(Environment)之间的交互机制。具体来说,Agent首先观测当前环境的状态,然后根据自身策略选择一个动作并执行;该动作被传递给环境后,环境据此更新状态,并将新的状态反馈给Agent。这一“感知—决策—执行—反馈”的循环过程,正是强化学习运行的基本模式。
这种持续的交互行为可以用一个数学模型来描述,即马尔科夫决策过程(MDP)。MDP是强化学习中最基础且最重要的理论框架之一。在该框架下,环境是完全可观测的(fully observable),意味着Agent能够准确获取当前所处的状态信息。
尽管现实中存在许多部分可观测的情况,但这类问题通常可以通过扩展或重构转化为标准的MDP形式进行处理。
1.1 马尔科夫特性(Markov Property)
在进入具体模型之前,我们需要先理解“马尔科夫特性”。它是所有马尔科夫类过程的基础前提。所谓马尔科夫特性,指的是:系统未来的状态转移仅依赖于当前状态,而与过去的历史状态无关。
假设Ht表示从初始时刻到时间t的所有历史状态序列,St表示当前状态,St+1表示下一时刻的状态。若满足:
P(St+1 | St, Ht) = P(St+1 | St)
则说明该过程具备马尔科夫特性。换句话说,未来与过去独立,只由现在决定。这一性质极大地简化了建模复杂度,也为后续的状态预测和价值计算提供了理论依据。

1.2 马尔科夫链(Markov Chain)
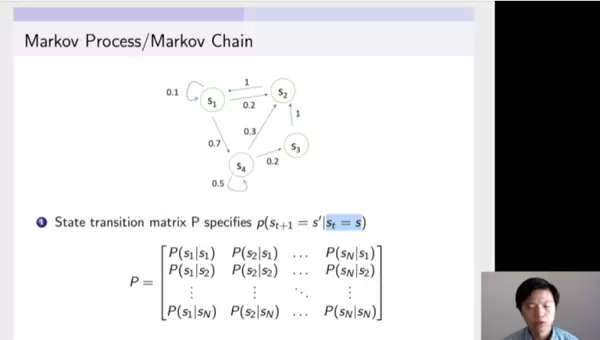
马尔科夫链是最简单的马尔科夫过程,仅包含状态及其转移概率,不涉及动作和奖励。下面我们通过一个实例来说明。
图中展示了四个状态S1、S2、S3、S4之间的转移关系。例如,当处于S1时,有0.1的概率保持在S1,0.2的概率转移到S2,0.7的概率跳转至S4。类似地,若当前状态为S4,则以0.3的概率进入S2,0.2的概率到达S3,0.5的概率维持原状态。
这些转移概率可以被组织成一个矩阵形式,称为状态转移矩阵。该矩阵每一行代表从某一特定状态出发,向所有可能下一状态转移的概率分布,本质上是一个条件概率分布P(St+1 | St)。
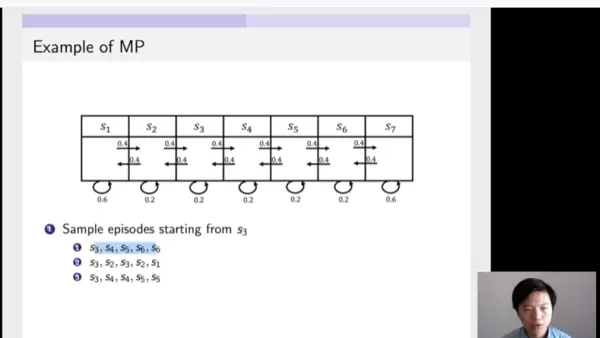
再看另一个例子,一个包含七个状态的马尔科夫链。各状态间的转移概率已明确列出。例如,从S1出发,有0.4的概率转移到S2,0.6的概率停留在S1;从S2出发,分别以0.4的概率向左到S1,0.4的概率向右到S3,0.2的概率保持不变。
一旦定义了完整的转移结构,就可以对该链进行多次采样,生成若干条状态轨迹。以下三条轨迹均从S3开始:
- 第一条:S3 → S4 → S5 → S6 → S6(停留)
- 第二条:S3 → S2 → S3 → S2 → S1
通过不断模拟,我们可以获得大量可能的状态路径,用于分析系统的长期行为趋势。
1.3 马尔科夫奖励过程(Markov Reward Process, MRP)
在马尔科夫链的基础上引入“奖励”(Reward)信号,就得到了马尔科夫奖励过程。MRP仍无动作干预,但在每个状态转移时会伴随一个即时奖励值。
因此,MRP可由四元组(S, P, R, γ)表示,其中S为状态集合,P为状态转移概率,R为期望奖励函数,γ为折扣因子。它保留了马尔科夫特性,同时允许我们对不同状态路径的累积收益进行量化评估。
通过引入价值函数的概念,我们可以衡量某个状态在未来所能带来的平均回报。这为后续引入策略和决策奠定了基础。
接下来我们来深入理解马尔可夫奖励过程。它本质上是在马尔科夫链的基础上引入了一个奖励函数所构成的模型。在该过程中,状态集合和状态之间的转移矩阵与传统马尔科夫链保持一致,不同之处在于新增了奖励机制。
这个奖励函数描述的是:当系统进入某一特定状态时,能够获得的期望奖励值。此外,还引入了一个重要的参数——折扣因子(通常用 γ 表示),我们将在后续内容中详细解释其作用。
假设我们沿用之前讨论过的马尔科夫链结构,现在为每个状态附加一个奖励值。例如,当系统到达状态 S1 时,可以获得 5 点奖励;到达状态 S7 时,则获得 10 点奖励;其余状态不提供任何奖励。由于状态空间是有限的,因此可以用一个向量来完整表示整个奖励函数,其中每一维对应一个状态的奖励大小。

我们可以借助一个形象的比喻来理解马尔可夫奖励过程:想象将一只纸船放入河流中,它会随着水流自然漂流,自身并无推进能力。这条河流的流向就相当于预设的状态转移路径,而纸船的轨迹则代表系统在不同状态间的演化过程。每当纸船漂至某个特定位置(即状态)时,就可能获得相应的奖励。整个过程就像随波逐流,完全依赖外部环境推动。

Horizon:指的是一个 episode(即一次完整的运行轨迹或游戏周期)的时间长度,由有限的时间步组成。这意味着整个过程不会无限延续,而是在一定步数后终止。
Return:指经过折扣处理后的累积奖励,也称为“回报”。它的计算方式是从当前时刻起,将未来所有获得的奖励按时间远近进行加权求和。越靠后的奖励,受到的衰减越大,体现在公式中就是乘以折扣因子的相应幂次。这反映了这样一个理念:相比遥远未来的收益,当前或近期的奖励更具价值。
State Value Function(状态价值函数):用于衡量在马尔可夫奖励过程中,某一状态的长期价值。它被定义为从该状态出发,未来所有折扣回报的期望值。这里的 Gt 即为之前定义的折扣回报序列。取期望的意义在于综合考虑从该状态出发可能经历的各种路径,从而得出一个平均意义上的“当前价值”。换句话说,当你进入某个状态时,这个值反映的就是你未来有望获得的总奖励在当前时刻的等效价值。





 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







