【模式识别与机器学习（9）】数据预处理-第一部分：数据基础认知

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

一、数据分类：认识三种数据形态

结构化数据类似于我们常见的Excel表格，其中信息被规整地排列在行与列中，每列代表一个特定属性，如姓名、年龄或工资。这类数据具有明确的格式和定义，属于高度组织化的类型。其主要特征包括：

• 强约束性：字段的位置、类型和含义固定不变；
• 易处理性：可直接通过SQL等数据库语言进行查询与分析；
• 存储方式：通常保存在关系型数据库中，以二维表形式存在。

典型的应用场景包括银行账户记录、学生成绩单以及商品库存清单等。

半结构化数据则介于结构化与非结构化之间，它具备一定的组织框架，但内容结构相对灵活。例如XML文档或HTML页面，虽然使用标签来标识内容，但标签的嵌套和数量可以动态变化。其特点如下：

• 弱约束性：存在基本结构，但允许字段扩展或缺失；
• 自描述性：数据本身携带结构信息（如通过标签）；
• 存储方式：常采用JSON、XML等格式存储。

实际应用包括网页源码、系统配置文件及API接口返回的JSON响应数据。

非结构化数据则是指没有统一格式或固定结构的信息，难以用传统表格方式表达。比如图像、音频、视频、Word文档或PDF文件等都属于此类。其特性为：

• 无约束性：缺乏标准化结构，内容组织自由；
• 难提取性：无法直接映射到数据库字段中；
• 存储方式：一般以文本文件或二进制文件形式保存。

常见实例有数码照片、录音文件、电子邮件正文和办公文档等。

1.4 三类数据的核心差异

这三类数据的根本区别在于模式（schema）对数据的约束程度：

• 结构化数据：遵循严格模式，所有数据必须符合预定义结构；
• 半结构化数据：拥有松散模式，支持结构弹性调整；
• 非结构化数据：无固定模式，完全自由组织。

从数据处理演进角度看，整体路径呈现为：从非结构化逐步向半结构化转化，再进一步结构化，最终发展至关联数据体系，进而支撑机器学习模型训练，并实现从数据分析到故事化表达，最终服务于智能决策的过程。

二、数据的基本统计描述：全面理解数据特征

掌握数据的整体分布情况是有效开展数据预处理的前提。基本统计方法有助于识别数据规律，发现异常值或离群点，从而为后续清洗与建模打下基础。

2.1 中心趋势度量：定位数据分布的中心位置

中心趋势用于反映一组数据集中最典型的数值位置，相当于“数据的重心”。

均值（Mean）是最常见的度量方式，即算术平均数。计算公式为：

\[ \bar{x} = \frac{1}{n}\sum_{i=1}^{n}x_i = \frac{x_1 + x_2 + \cdots + x_n}{n} \]

根据应用场景不同，均值可分为：

• 算术平均：各数值等权相加后除以总数；
• 加权平均：赋予不同数值相应权重后再计算；
• 截尾平均：剔除极端值后的平均值，提升稳健性。

需要注意的是，均值对离群点非常敏感。例如，在计算班级平均成绩时，若有一名学生取得极高分数，会导致整体均值偏高，可能无法真实反映大多数学生的水平。

中位数（Median）是指将数据按大小顺序排列后处于正中间的数值。当样本量为偶数时，取中间两个数的平均值。对于偏态分布的数据（如收入），中位数比均值更具代表性，因为它不受极值影响。

举例来说，在分析城市居民收入水平时，少数高收入者会显著拉高平均值，而中位数更能体现普通民众的实际收入状况。缺点是计算需要排序，当数据规模庞大时，运算成本较高。

众数（Mode）是数据集中出现频率最高的值。依据分布形态可分为：

• 单峰（unimodal）：仅有一个众数；
• 双峰（bimodal）：存在两个明显的峰值；
• 三峰（trimodal）：出现三个高频值区域。

众数适用于类别型数据或需要找出最常见取值的场景，且不受极端值干扰，但在多峰或均匀分布中可能不具代表性。

2.2 数据散布度量：评估数据的离散程度

除了中心位置，了解数据的分散情况同样重要。常用的散布度量包括极差、方差、标准差和四分位距（IQR）等。

• 极差：最大值与最小值之差，简单直观但易受异常值影响；
• 方差与标准差：衡量数据偏离均值的程度，标准差为方差的平方根，单位与原数据一致；
• 四分位距（IQR）：第三四分位数（Q3）减去第一四分位数（Q1），反映中间50%数据的波动范围，抗噪能力强。

这些指标帮助判断数据是否集中或广泛分布，也为识别离群点提供依据。

2.3 图形化展示：可视化数据分布特征

图形显示能更直观地展现数据的分布形态与潜在问题。

• 直方图：显示连续变量的频数分布，揭示数据形状（如正态、偏态）；
• 箱线图：展示五数概括（最小值、Q1、中位数、Q3、最大值），突出离群点；
• 散点图：观察两个变量之间的关系趋势；
• 饼图/条形图：适用于分类变量的频率比较。

三、数据预处理的必要性：为何要进行数据清洗

3.1 真实世界中的数据往往是“脏”的

现实环境下的数据普遍存在质量问题，表现为缺失值、噪声、重复记录、不一致格式或错误输入等。这些问题直接影响分析结果的准确性与模型性能。因此，必须通过数据清洗、填补、去重和校验等手段提升数据质量。

3.2 学习算法对输入数据的要求较高

大多数机器学习算法假设输入数据是规范、完整且分布合理的。原始数据往往不符合这些前提条件，例如：

• 含有缺失值会影响参数估计；
• 量纲差异大会导致某些特征权重被放大；
• 类别不平衡会误导分类器判断。

因此，需通过归一化、标准化、编码转换等方式对数据进行预处理，使其满足算法需求，提高建模效果。

第一部分总结

本部分内容围绕数据预处理的基础知识展开，涵盖三大核心方面：

1. 理解不同类型的数据——结构化、半结构化与非结构化，及其各自的特点与存储方式；
2. 掌握数据的基本统计描述方法，包括中心趋势与离散程度的度量，以及图形化呈现技术；
3. 明确数据预处理的重要性，认识到真实数据的复杂性以及算法对高质量输入的依赖。

这些内容构成了数据科学工作的起点，为后续的数据清洗、集成、变换与建模奠定了坚实基础。

在统计学中，众数是指数据中出现频率最高的数值。当一组数据中有三个值同时具有最高频次时，则称其为“有三个众数”。例如，在调查“最喜欢的颜色”这一问题时，若“蓝色”的选择次数最多，则“蓝色”即为该数据集的众数。此外，对于单峰且适度偏斜（非对称）的数值型数据，存在一个经验性近似公式：均值与众数之差约等于三倍的（均值与中位数之差），即：均值 - 众数 ≈ 3 × (均值 - 中位数)。

**中位数（Midrange）** 指的是数据集中最大值与最小值的算术平均数，计算公式为：
中位数 = (max + min) / 2。
尽管计算简单，但该指标极少被采用，因为它极易受到极端值的影响，缺乏稳健性。

2.2 数据散布程度的度量方法

衡量数据的离散程度有助于理解数据分布的扩展范围，类似于观察一群人身高之间的差异。

**极差（Range）** 是描述数据分散最基础的指标之一，定义为最大值减去最小值：
极差 = max - min。
虽然直观易懂，但极差仅依赖于两个端点值，忽略了中间数据的分布情况，因此信息有限。

**分位数（Quantile）** 是将有序数据按比例划分为若干连续部分的方法。其中最常用的是四分位数：

• Q1（第1四分位数）：也称第25百分位数，表示有25%的数据小于或等于该值；
• Q2（第2四分位数）：即中位数，对应第50百分位数，一半数据在其下方；
• Q3（第3四分位数）：即第75百分位数，75%的数据小于此值。

基于此，**四分位数极差（IQR）** 定义为 Q3 与 Q1 的差值：
IQR = Q3 - Q1，
它反映了中间50%数据的波动范围，抗异常值能力强。

对于非对称或倾斜分布的数据，单一的离散度指标可能不够全面。此时可使用**五数概括（Five-Number Summary）** 来更完整地描述数据分布特征，包括以下五个关键数值：

1. 最小值（Minimum）
2. 第一四分位数（Q1）
3. 中位数（Median）
4. 第三四分位数（Q3）
5. 最大值（Maximum）

相邻两个数值之间大约涵盖25%的数据项。例如，对一组按升序排列的月薪样本（单位：元）：2210, 2255, 2350, 2380, 2380, 2390, 2420, 2440, 2450, 2550, 2630, 2825，其五数概括结果为：Min = 2210，Q1 = 2365，Median = 2405，Q3 = 2500，Max = 2825。

**盒图（Boxplot）** 由统计学家 John W. Tukey 提出，是一种可视化展示五数概括的有效工具。其结构包括：

• 盒子的两端分别位于 Q1 和 Q3 处，盒长即为 IQR；
• 盒内一条线表示中位数的位置；
• 从盒子延伸出的“胡须”（whiskers）连接至最小和最大观测值；
• 若某数据点偏离四分位区间超过 1.5×IQR，则被视为离群点，并单独标出。

实际应用中，盒图常用于比较不同组别的数据分布，如多个班级的成绩对比。然而，面对大规模数据集时，绘制清晰有效的盒图仍面临一定挑战。

**方差与标准差** 是衡量数据围绕均值波动的核心指标。

方差的计算公式为：
σ = (1/n) Σ(xi - x)，
表示每个数据点与均值偏差的平方的平均值。

标准差是方差的平方根：
σ = √σ，
由于其单位与原始数据一致，解释起来更加直观。

例如，在质量控制过程中，较小的标准差意味着产品性能更为稳定，生产过程的一致性更高。

2.3 基本统计描述的图形化呈现方式

通过图形手段可以更直观地揭示数据分布特性。

**分位数图（Quantile Plot）** 将每个观测值 xi 与其对应的百分位 fi 配对，表明约有 fi×100% 的数据小于该值。这种图表有助于观察整体数据在各分位点上的分布趋势。

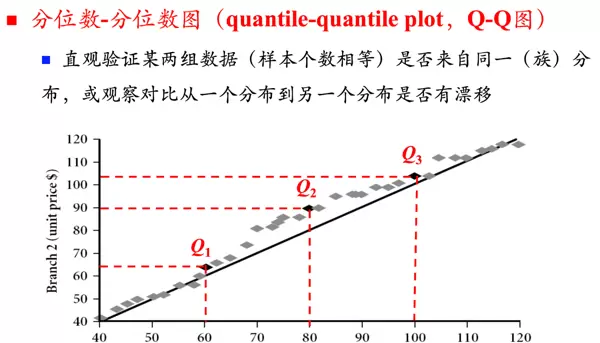
**分位数-分位数图（Q-Q图）** 用于判断两组数据是否来自同一类分布，或检测分布之间是否存在偏移。若两组数据服从相同分布，则图中各点应大致落在一条直线上。

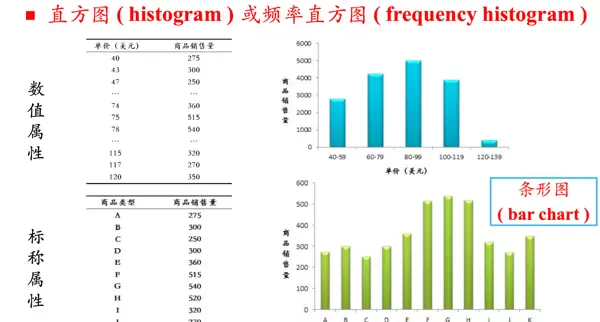
**直方图（Histogram）** 又称频率直方图，利用矩形条的高度表示各区间内数据出现的频数或频率。适用于数值型变量；而分类属性则更适合使用条形图（bar chart）。直方图能清晰反映数据分布形态，如是否对称、左偏或右偏。

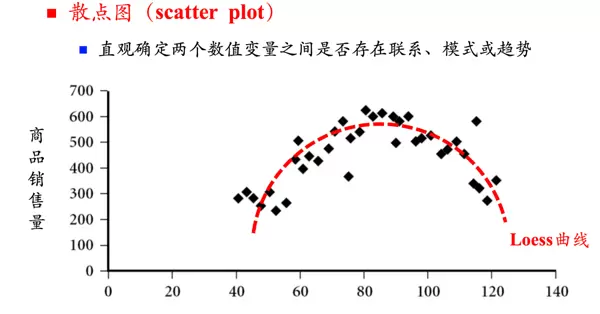
**散点图（Scatter Plot）** 用于展示两个变量之间的关系，通过点的分布模式识别相关性、聚集性或异常模式，是探索双变量数据结构的重要工具。

散点图是一种有效的可视化工具，用于判断两个数值型变量之间是否存在某种关联、规律或趋势。例如，在分析商品销售情况时，可以通过绘制销售量与单价之间的散点图，来观察二者是否具有相关性。若数据中呈现出一定的趋势特征，还可以进一步添加Loess曲线以更清晰地展现变化趋势。

三、为何需要进行数据预处理

关键词：脏数据、不完整数据、噪声数据、不一致数据、过拟合、欠拟合、交叉验证

3.1 现实中的数据通常存在质量问题

在实际应用中，来自真实世界的数据往往不够“干净”，不能直接投入机器学习模型的训练过程，必须经过清洗和整理。常见的问题包括以下几类：

不完整性（Incomplete Data）：指部分数据缺失了某些属性值，或者缺少关键字段，甚至只提供了聚合后的信息。例如：

occupation = ""

——职业信息为空；或是缺乏对分析至关重要的其他属性。

噪声数据（Noisy Data）：表示数据中包含错误记录或异常值。典型例子如：

Salary = "-10"

——工资字段出现负数，显然不符合现实逻辑；也可能是人为录入时产生的误差。

不一致性（Inconsistent Data）：指的是同一含义的信息在不同地方使用了不同的编码或命名方式。具体表现包括：

1. age = "42"

   与

   birthday = "03/07/1997"

   中显示的年龄与出生日期相互矛盾；
2. 评分标准前后不统一，之前使用“1, 2, 3”等级，现在改为“A, B, C”；
3. 重复记录之间存在差异，比如

   name="haha" income="42$"

   和

   name="haha" income="24$"

   所示的数据条目内容不一致。

3.2 学习算法的选择及其参数设定

没有万能的算法：并不存在适用于所有场景的最优模型，合适的方法取决于具体的数据特征。

在建模过程中需警惕两类常见问题：

• 过拟合（Overfitting）：模型在训练集上表现极佳，但泛化能力差，面对新样本时性能显著下降；
• 欠拟合（Underfitting）：模型过于简单，无法有效捕捉数据中的潜在模式。

关于测试数据的构建策略：

• 当数据资源充足时，可划分出独立于训练集的大规模测试集；
• 若数据有限，则推荐采用交叉验证（Cross Validation）方法，提升评估结果的稳定性与可靠性。

核心观点强调：机器学习并非简单地将某个算法套用到数据集上即可完成任务。每一个问题都有其独特性，必须深入理解数据背后的含义，从多个维度进行探索，并创造性地选择合适的建模视角。

第一部分内容小结

通过本阶段的学习，我们已掌握数据预处理的基本框架：

• 数据类型分类：明确了结构化、半结构化与非结构化数据的区别，了解各类数据在组织形式和存储方式上的特点；
• 统计描述方法：掌握了如何利用均值、中位数、方差等统计指标概括数据特征，并学会使用直方图、散点图等图形手段实现数据可视化；
• 预处理必要性认知：认识到原始数据常存在缺失、噪声和不一致等问题，同时理解了过拟合与欠拟合的概念及其影响。

这些基础知识为后续深入学习具体的预处理技术奠定了坚实基础。接下来的第二部分，我们将重点探讨缺失值处理、数据清洗与集成方法，以及属性选择与转换的相关技巧。

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：数据预处理 机器学习 模式识别 预处理 consistent

相关内容：机器学习数据处理